
题目列表(包括答案和解析)
2、(1)A(2,2),直线 :
: ,B(-3,
,B(-3, )
)

 ,
,
(2)
(3)A(2,2),∠AOY=∠YOQ=450,直线OQ: ,Q(-1,1),AQ=
,Q(-1,1),AQ= ,△AOQ外接圆面积=
,△AOQ外接圆面积= (平方单位)
(平方单位)
5、如图,P为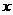 轴正半轴上一点,半圆P交
轴正半轴上一点,半圆P交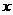 轴于A、B两点,交
轴于A、B两点,交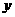 轴于C点,弦AE分别交OC、CB于点D、F,已知
轴于C点,弦AE分别交OC、CB于点D、F,已知 。
。
 (1)求证:AD=CD; (2)若DF=
(1)求证:AD=CD; (2)若DF= ,tan∠ECB=
,tan∠ECB= ,求经过A、B、C三点的抛物线的解析式;
,求经过A、B、C三点的抛物线的解析式;
(3)设M为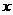 轴负半轴上一点,OM=
轴负半轴上一点,OM= AE,是否存在过点M的直线,使该直线与(2)中所得的抛物线的两个交点到
AE,是否存在过点M的直线,使该直线与(2)中所得的抛物线的两个交点到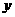 轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由。
轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由。
3-6 函数的综合运用
4、 如图,直线
如图,直线 与
与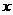 轴、
轴、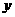 轴交于点A、B,⊙M经过原点O及A、B两点。
轴交于点A、B,⊙M经过原点O及A、B两点。
(1)求以OA、OB两线段长为根的一元二次方程;
(2)C是⊙M上一点,连结BC交OA于点D,若∠COD=∠CBO,写出经过O、C、A三点的二次函数解析式;
(3)若延长BC到E,使DE=2,连结AE,试判断直线EA与⊙M的位置关系,并说明理由。
3、 如图,抛物线
如图,抛物线 经过A、B、C三点,顶点为D,且与
经过A、B、C三点,顶点为D,且与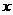 轴的另一个交点为E。
轴的另一个交点为E。
(1)求抛物线 的解析式;
的解析式;
(2)求四边形ABDE的面积;
(3)△AOB与△BDA是否相似,如果相似,请予以证明;如果不相似,请说明理由。
(4)设抛物线 的对称轴与
的对称轴与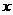 轴交于点F,另一条抛物线
轴交于点F,另一条抛物线 经过点E(抛物线
经过点E(抛物线 与抛物线
与抛物线 不重合),且顶点为M(
不重合),且顶点为M(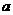 ,
,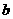 ),对称轴与
),对称轴与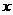 轴交于点G,且以M、G、E为顶点的三角形与以D、E、F为顶点的三角形全等,求
轴交于点G,且以M、G、E为顶点的三角形与以D、E、F为顶点的三角形全等,求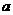 、
、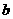 的值(只须写出结果,不必写出解答过程)。
的值(只须写出结果,不必写出解答过程)。
2、 如图,已知直线
如图,已知直线 与
与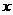 轴交于点P(-1,0),与
轴交于点P(-1,0),与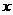 轴所夹的锐角为
轴所夹的锐角为 ,县tan
,县tan =
=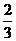 ,直线
,直线 与抛物线
与抛物线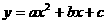
 交于点A(
交于点A( ,2)和点B(-3,
,2)和点B(-3, )
)
(1)求A、B两点的坐标,并用含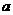 的代数式表示
的代数式表示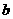 和
和 ;
;
(2)设关于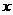 的方程
的方程 的两实数根为
的两实数根为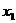 、
、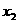 ,且
,且 ,
, ,求此时抛物线的解析式;
,求此时抛物线的解析式;
(3)若点Q是由(2)所得的抛物线上一点,且在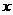 轴上方,当满足∠AOQ=900时,求点Q的坐标及△AOQ外接圆的面积。
轴上方,当满足∠AOQ=900时,求点Q的坐标及△AOQ外接圆的面积。
1、 汽车在行驶中,由于惯性作用,刹车后还要向前滑行一段距离才能停住,我们称这段距离为“刹车距离”。刹车距离是分析事故的一个重要因素,在一个限速40千米/小时以内的弯道上,甲、乙两车相向而行,发情况不对,同时刹车,但还是相碰了。事后现场测得甲车的刹车距离为12米,乙车的刹车距离超过10米,但小于12米。查有关资料知:甲种车的刹车距离
汽车在行驶中,由于惯性作用,刹车后还要向前滑行一段距离才能停住,我们称这段距离为“刹车距离”。刹车距离是分析事故的一个重要因素,在一个限速40千米/小时以内的弯道上,甲、乙两车相向而行,发情况不对,同时刹车,但还是相碰了。事后现场测得甲车的刹车距离为12米,乙车的刹车距离超过10米,但小于12米。查有关资料知:甲种车的刹车距离 (米)与车速
(米)与车速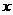 (千米/小时)之间有下列关系,
(千米/小时)之间有下列关系, ;乙种车的刹车距离
;乙种车的刹车距离 (米)与车速
(米)与车速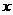 (千米/小时)的关系如图所示。请你就两车的速度方面分析相碰的原因。
(千米/小时)的关系如图所示。请你就两车的速度方面分析相碰的原因。
4、已知抛物线 与
与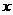 轴交于A、B两点,顶点为C,连结AC、BC,点A1、A2、A3、…
轴交于A、B两点,顶点为C,连结AC、BC,点A1、A2、A3、… 把AC
把AC 等分,过各分点作
等分,过各分点作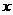 轴的平行线,分别交BC于B1、B2、B3、…
轴的平行线,分别交BC于B1、B2、B3、… ,线段A1B1、A2B2、A3B3、…、
,线段A1B1、A2B2、A3B3、…、 的和为
。(用含
的和为
。(用含 的式子表示)
的式子表示)
3、将抛物线 绕顶点旋转1800,再沿对称轴平移,得到一条与直线
绕顶点旋转1800,再沿对称轴平移,得到一条与直线 交于点(2,
交于点(2, )的新抛物线,新抛物线的解析式为
。
)的新抛物线,新抛物线的解析式为
。
2、已知M、N两点关于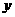 轴对称,且点M在双曲线
轴对称,且点M在双曲线 上,点N在直线
上,点N在直线 上, 设点M(
上, 设点M(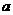 ,
,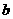 ),则抛物线
),则抛物线 的顶点坐标为
。
的顶点坐标为
。
1、函数 的图像与
的图像与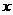 轴有且只有一个交点,那么
轴有且只有一个交点,那么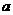 的值是 ,与
的值是 ,与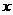 轴的交点坐标为
。
轴的交点坐标为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com