
题目列表(包括答案和解析)
4.二次函数y=ax^2+bx+c的图象
第1题. 把函数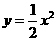 的图像向 平移 个单位即可得
的图像向 平移 个单位即可得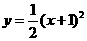 的图像;后一个函数图像的顶点坐标为 ,对称轴方程为 .
的图像;后一个函数图像的顶点坐标为 ,对称轴方程为 .
答案:左 1 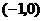
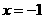
第2题. 把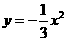 的图像向 平移 个单位得
的图像向 平移 个单位得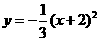 的图像;第二个函数图像的顶点坐标为 ,对称轴为 .
的图像;第二个函数图像的顶点坐标为 ,对称轴为 .
答案:左 2 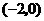
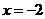
第3题. 把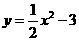 的图像向 平移 个单位得
的图像向 平移 个单位得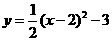 的图像,再向 平
的图像,再向 平
移 个单位得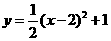 的图像.
的图像.
答案:右 2 上 4
第4题. 抛物线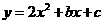 的顶点坐标是
的顶点坐标是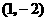 ,则
,则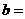 ,
,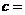 .
.
答案: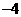 0
0
第5题. 抛物线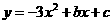 是由抛物线
是由抛物线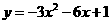 向上平移3个单位,再向左平移2个单位得到的,则
向上平移3个单位,再向左平移2个单位得到的,则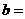 ,
,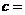 .
.
答案: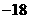
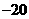
第6题. 二次函数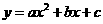 中,
中,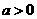 ,
,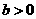 ,
,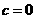 ,则其图像的顶点坐标为第 象限.
,则其图像的顶点坐标为第 象限.
答案:三
第7题. 抛物线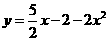 的开口向 ,对称轴方程为 ,顶点坐标为 .
的开口向 ,对称轴方程为 ,顶点坐标为 .
答案:下 
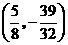
第8题. 函数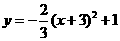 ,当
,当 时,
时, 随
随 增大而减小,当
增大而减小,当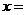 时,
时, 有最 值
有最 值
是 .
答案: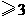
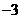 大 1
大 1
第9题. 将函数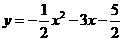 的图像向下平移2个单位,再向右平移3个单位,得到函数 的图像.
的图像向下平移2个单位,再向右平移3个单位,得到函数 的图像.
答案: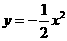
第10题. 若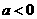 ,
,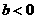 ,
, ,则
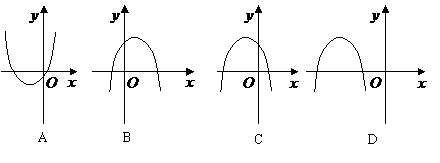
,则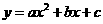 的图像是( )
的图像是( )
答案:C
第11题. 在同一直角坐标系中,直线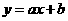 和抛物线
和抛物线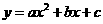 的图像只可能是( )
的图像只可能是( )
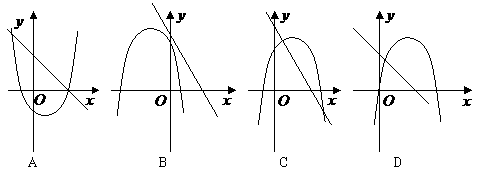
答案:C
第12题. 已知二次函数 (
(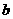 ,
,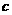 为常数).
为常数).
(1)若二次函数的图像经过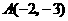 和
和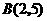 两点,求此二次函数的函数式;
两点,求此二次函数的函数式;
(2)若(1)中的二次函数的图像过点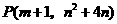 ,且
,且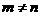 ,求
,求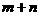 的值.
的值.
答案:(1)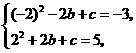 解得
解得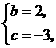
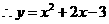 .
.
(2)二次函数的图象过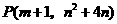 ,
,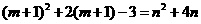 ,
,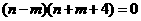 ,
,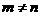 ,
,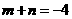 .
.
第13题. 已知关于 的二次函数
的二次函数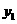 和
和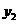 ,其中
,其中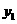 的图像开口向下,与
的图像开口向下,与 轴交于
轴交于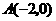 和
和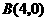 ,对称轴平行于
,对称轴平行于 轴,其顶点与
轴,其顶点与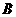 点距离为5,而
点距离为5,而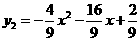 .
.
(1)求二次函数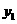 的函数式;
的函数式;
(2)把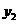 化为
化为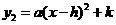 的形式;
的形式;
(3)把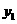 的图像经过怎样平移得到
的图像经过怎样平移得到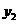 的图像.
的图像.
答案:(1)对称轴与 轴交点为
轴交点为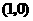 ,顶点
,顶点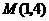 ,用待定系数法,求得
,用待定系数法,求得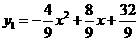 .
.
(2)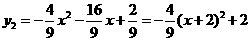 .
.
(3)把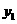 的图像向下平移2个单位,再向左平移3个单位得到
的图像向下平移2个单位,再向左平移3个单位得到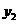 的图像.
的图像.
第14题. 已知二次函数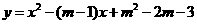 ,其中
,其中 为实数.
为实数.
(1)若其图像过原点,求函数式;
(2)怎样平移此函数图像,使它在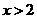 时,
时, 随
随 的增大而增大,在
的增大而增大,在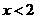 时,
时, 随
随 的增大而减小.
的增大而减小.
答案:(1)图像过原点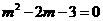 ,
,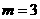 或
或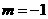 .当
.当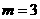 时,
时,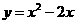 ;当
;当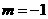 时,
时,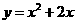 .
.
(2)将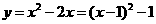 向右平移1个单位,得
向右平移1个单位,得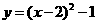 符合要求;
符合要求;
将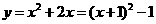 向右平移3个单位,得
向右平移3个单位,得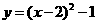 符合要求.
符合要求.
第15题. 已知函数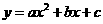 的图像如图所示,关于系数
的图像如图所示,关于系数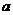 ,
,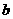 ,
,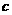 有下列不等式①
有下列不等式①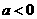 ,②
,②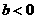 ,③
,③ ,④
,④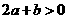 ,⑤
,⑤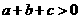 ,其中正确的不等式序号是 (注:把你认为正确的不等式序号都填上).
,其中正确的不等式序号是 (注:把你认为正确的不等式序号都填上).
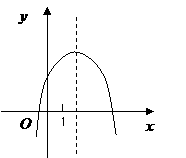
答案:①③④⑤
第16题. 如果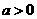 ,
,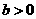 ,
, ,
,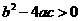 ,那么抛物线
,那么抛物线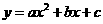 经过 象限.
经过 象限.
答案:一、二、三
第17题. 二次函数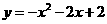 的顶点坐标、对称轴方程分别是( )
的顶点坐标、对称轴方程分别是( )
A.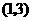 ,
,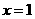 B.
B.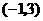 ,
,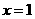
C.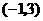 ,
,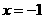 D.
D.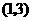 ,
,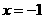
答案:C
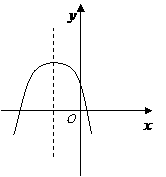 第18题. 若二次函数
第18题. 若二次函数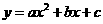 的图像如图所示,则直线
的图像如图所示,则直线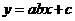 不经过 象限.
不经过 象限.
答案:第四
第19题. 抛物线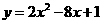 的顶点为
的顶点为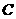 点,已知函数
点,已知函数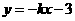 的图像经过
的图像经过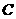 点,则它与两坐标轴所围成的三角形面积为 .
点,则它与两坐标轴所围成的三角形面积为 .
答案: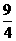
第20题. 抛物线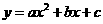 经过四个象限,且顶点在第三象限,则
经过四个象限,且顶点在第三象限,则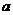 ,
,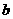 ,
,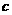 ,
,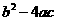 与0比较大小分别为
与0比较大小分别为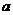 0,
0,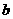 0,
0,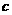 ,
,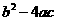 0.
0.
答案:



第21题. 将抛物线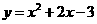 向左平移4个单位,再向下平移3个单位,所得抛物线的函数表达式为 .
向左平移4个单位,再向下平移3个单位,所得抛物线的函数表达式为 .
答案: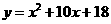
第22题. 关于二次函数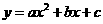 的图像有下列命题:①当
的图像有下列命题:①当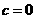 时,函数的图像经过原点;②当
时,函数的图像经过原点;②当 ,且函数的图像开口向下时,方程
,且函数的图像开口向下时,方程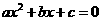 必有两个不相等的实根;③函数图像最高点的纵坐标是
必有两个不相等的实根;③函数图像最高点的纵坐标是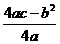 ;④当
;④当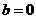 时,函数的图像关于
时,函数的图像关于 轴对称.
轴对称.
其中正确命题的个数是( )
A.1个 B.2个 C.3个 D.4个
答案:C
第23题. 简述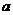 ,
,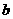 ,
,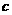 在二次函数
在二次函数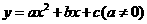 图像中的作用.
图像中的作用.
答案: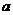 的正负决定抛物线开口方向,
的正负决定抛物线开口方向, 大小决定抛物线开口大小;
大小决定抛物线开口大小;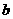 与
与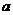 共同决定抛物线对称轴;
共同决定抛物线对称轴;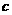 的值决定抛物线与
的值决定抛物线与 轴交点的纵坐标,
轴交点的纵坐标,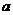 ,
,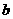 ,
,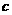 的值共同确定抛物线顶点纵坐标.
的值共同确定抛物线顶点纵坐标.
第24题. 求二次函数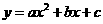 图像的顶点坐标和对称轴有三种不同方法,它们分别是(1) ,即 ;(2) ,即 ;(3) ,即 .
图像的顶点坐标和对称轴有三种不同方法,它们分别是(1) ,即 ;(2) ,即 ;(3) ,即 .
答案:公式法 顶点是 ,对称轴是直线
,对称轴是直线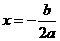
配方法 化为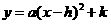 的形式 顶点是
的形式 顶点是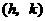 ,对称轴是直线
,对称轴是直线 运用抛物线对称性 对称点连线的垂直平分线为对称轴 对称轴与抛物线交点为顶点
运用抛物线对称性 对称点连线的垂直平分线为对称轴 对称轴与抛物线交点为顶点
第25题. 二次方程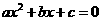 的两根为
的两根为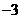 和
和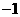 ,则对应二次函数
,则对应二次函数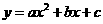 的对称轴为( )
的对称轴为( )
A.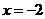 B.
B.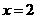 C.
C.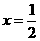 D.
D.
答案:A
第26题. 二次函数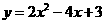 配方可得
配方可得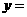 ,其图像是 .
,其图像是 .
答案: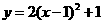 ,抛物线
,抛物线
第27题. 点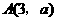 在二次函数
在二次函数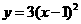 的图像上,则
的图像上,则 .
.
答案:12
第28题. 二次函数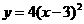 的顶点坐标是 ,对称轴为 .
的顶点坐标是 ,对称轴为 .
答案:(3,0),直线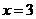
第29题. 二次函数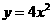 ,
,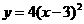 和
和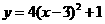 的图象, 相同, 不同.
的图象, 相同, 不同.
答案:形状,位置
第30题. 二次函数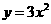 图像由二次函数
图像由二次函数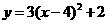 的图像经过怎样的平移得到?
的图像经过怎样的平移得到?
答案:向左平移4个单位,再向下平移2个单位
第31题. 对于二次函数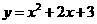 ,函数值
,函数值 的取值范围是( )
的取值范围是( )
A. B.
B.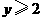 C.
C.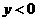 D.
D.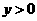
答案:B
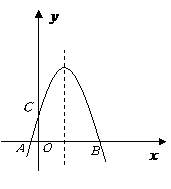 第32题. 下图是二次函数
第32题. 下图是二次函数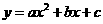 的图像,则下列说法错误的是( )
的图像,则下列说法错误的是( )
A.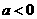 B.对称轴是直线
B.对称轴是直线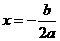
C.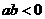 D.
D.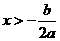 时,
时, 随
随 的增大而增大
的增大而增大
答案:D
第33题. 已知抛物线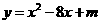 的最小值是1,求
的最小值是1,求 的值和抛物线的顶点坐标.
的值和抛物线的顶点坐标.
答案: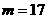 ,(4,1)
,(4,1)
第34题. 已知抛物线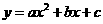 与
与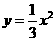 的形状相同,开口方向相反,顶点坐标是(
的形状相同,开口方向相反,顶点坐标是(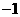 ,4),求
,4),求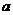 ,
,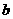 ,
,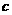 的值.
的值.
答案: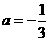 ,
,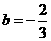 ,
,
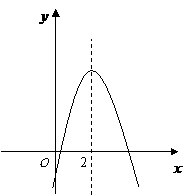 第35题. 如图,是二次函数
第35题. 如图,是二次函数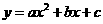 的图像,已知
的图像,已知 的最大值是4.5,则抛物线的顶点坐标是( )
的最大值是4.5,则抛物线的顶点坐标是( )
A.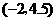 B.
B.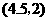
C.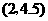 D.
D.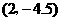
答案:C
第36题. 二次函数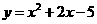 取最小值时,自变量
取最小值时,自变量 的值是( )
的值是( )
A.2 B.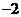 C.1 D.
C.1 D.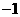
答案:D
第37题. 二次函数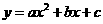 有最大值8,则方程
有最大值8,则方程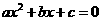 的根的情况是 .
的根的情况是 .
答案:两个不同实数根
第38题. 已知二次函数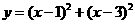 ,当
,当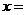 时,函数达到最小值.
时,函数达到最小值.
答案:2
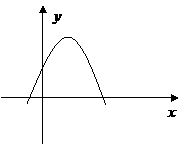 第39题. 二次函数
第39题. 二次函数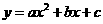 的图象如图所示,那么下列四个结论:①
的图象如图所示,那么下列四个结论:①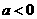 ;②
;② ;③
;③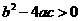 ;④
;④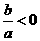 中,正确的结论有( )
中,正确的结论有( )
A.1个 B.2个 C.3个 D.4个
答案:D
第40题. 将抛物线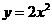 如何平移可得到抛物线
如何平移可得到抛物线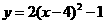 ( )
( )
A.向左平移4个单位,再向上平移1个单位
B.向左平移4个单位,再向下平移1个单位
C.向右平移4个单位,再向上平移1个单位
D.向右平移4个单位,再向下平移1个单位
答案:D
第41题. 已知二次函数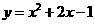 ,
,
(1)求出函数图象上5个点的坐标,并画出函数的图像;
(2)指出该函数的开口方向,顶点坐标及对称轴.
解:(1)列表:


(2)描点作图:
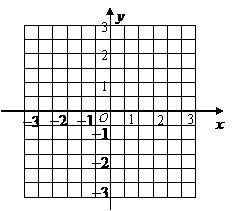
答案:(1)略(2)开口向上,(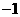 ,
,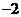 ),直线
),直线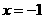
第42题. 抛物线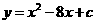 的顶点在
的顶点在 轴上,则
轴上,则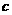 的值为 .
的值为 .
答案:16
第43题. 把二次函数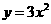 的图像向左平移2个单位,再向上平移1个单位,所得到的图象对应的二次函数关系是( )
的图像向左平移2个单位,再向上平移1个单位,所得到的图象对应的二次函数关系是( )
A.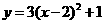 B.
B.
C.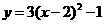 D.
D.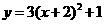
答案:D
第44题. 将抛物线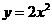 如何平移可得到抛物线
如何平移可得到抛物线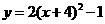 ( )
( )
A.向右平移4个单位,再向上平移1个单位
B.向左平移4个单位,再向下平移1个单位
C.向右平移4个单位,再向上平移1个单位
D.向右平移4个单位,再向下平移1个单位
答案:B
第45题. 抛物线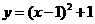 的顶点坐标是( )
的顶点坐标是( )
A.(1,1) B.(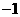 ,1) C.(1,
,1) C.(1,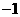 ) D.(
) D.(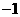 ,
,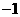 )
)
答案:A
第46题. 二次函数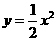 的图象向左平移1个单位,再向下平移3个单位后,所得抛物线的函数表达式是( )
的图象向左平移1个单位,再向下平移3个单位后,所得抛物线的函数表达式是( )
A.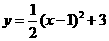 B.
B.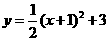
C.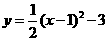 D.
D.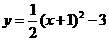
答案:D
第47题. 二次函数 的图象的顶点坐标是 .
的图象的顶点坐标是 .
答案: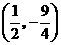
第48题. 已知二次函数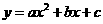 的图象过点
的图象过点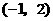 ,并且
,并且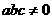 ,试写出一个满足条件的函数的表达式 .
,试写出一个满足条件的函数的表达式 .
答案: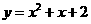
第49题. 已知抛物线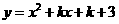 ,根据下面的条件,求
,根据下面的条件,求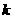 的值.
的值.
(1)抛物线的顶点在 轴上;
轴上;
(2)抛物线的顶点在 轴上;
轴上;
(3)抛物线的对称轴是直线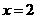 ;
;
(4)抛物线经过原点.
答案:(1) 顶点在
顶点在 轴上,
轴上, 对称轴为
对称轴为 轴,
轴,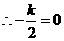 ,
,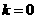 .
.
(2) 顶点在
顶点在 轴上,
轴上, 顶点的纵坐标为0,即
顶点的纵坐标为0,即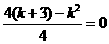 ,
,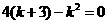 ,
,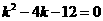 ,
,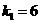 ,
,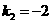 ,即
,即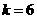 或
或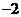 .
.
(3)由 得
得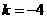 .
.
(4)将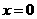 ,
,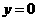 代入原关系式中得
代入原关系式中得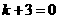 ,
,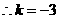 .
.
第50题. 如图,某二次函数图象的顶点坐标是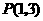 .问:
.问: 取哪些值时,函数
取哪些值时,函数 的值随
的值随 的增大而增大?
的增大而增大? 取哪些值时,函数
取哪些值时,函数 的值随
的值随 的增大而减小?
的增大而减小?
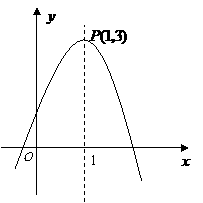
答案:当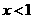 时,
时, 随
随 的增大而增大;当
的增大而增大;当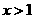 时,
时, 随
随 的增大而减小.
的增大而减小.
第51题. 二次函数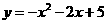 ,当 时,
,当 时, 随
随 的增大而增大,当 时,
的增大而增大,当 时, 随
随 的增大而减不,当 时,
的增大而减不,当 时, 有最大值 .
有最大值 .
答案: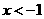
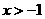
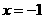 6
6
第52题. 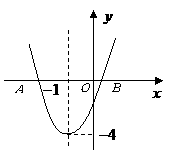 二次函数
二次函数 的图象如图所示,则函数值
的图象如图所示,则函数值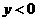 时,对应的
时,对应的 的取值范围是 .
的取值范围是 .
答案: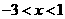
第53题. 已知抛物线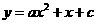 与
与 轴的交点的横坐标是
轴的交点的横坐标是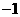 ,则
,则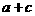 的值为 .
的值为 .
答案:1
第54题. 已知抛物线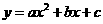 的对称轴为2,且经过点
的对称轴为2,且经过点 ,则
,则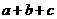 的值( )
的值( )
A.等于0 B.等于1 C.等于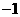 D.不能确定
D.不能确定
答案:A
第55题. 汽车行驶中,由于惯性作用,刹车后还要向前滑行一段距离才能停止,我们称这段距离为“刹车距离”.刹车距离是分析交通事故的一个重要因素.在一个限速 以内的弯道上,甲、乙两车相向而行,因为两司机发现情况不对,所以同时刹车,但还是相撞了,事后现场测得甲车的刹车距离为
以内的弯道上,甲、乙两车相向而行,因为两司机发现情况不对,所以同时刹车,但还是相撞了,事后现场测得甲车的刹车距离为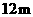 ,乙车的刹车距离超过
,乙车的刹车距离超过 ,但小于
,但小于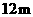 .查有关资料知:甲车的刹车距离
.查有关资料知:甲车的刹车距离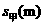 与车速
与车速 之间有下列关系:
之间有下列关系: ;乙车的刹车距离
;乙车的刹车距离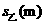 与车速
与车速 的关系如图所示.
的关系如图所示.
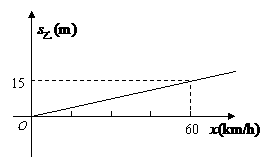
请你从两车的速度方面分析相撞的原因.
答案:解方程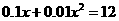 得
得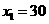 ,
,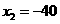 (舍去),故甲车的速度是
(舍去),故甲车的速度是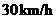 ,未超过限速.由图像知
,未超过限速.由图像知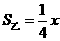 ,由
,由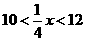 得
得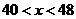 .故乙车超速了,即原因在乙车超速行驶.
.故乙车超速了,即原因在乙车超速行驶.
第56题. 抛物线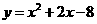 的顶点坐标是 ,与
的顶点坐标是 ,与 轴的交点坐标是 .
轴的交点坐标是 .
答案: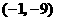
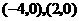
第57题. 已知矩形窗户的周长为 ,试写出窗户面积
,试写出窗户面积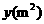 与窗户宽
与窗户宽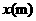 之间的函数关系,并用图象表示
之间的函数关系,并用图象表示 随
随 变化而变化的规律.
变化而变化的规律.
答案:
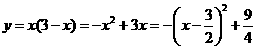 .用图象表示这个规律如图所示.
.用图象表示这个规律如图所示.
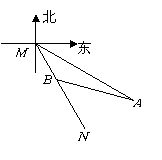
第58题. 如图,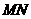 表示某引水工程的一段设计路线,从
表示某引水工程的一段设计路线,从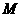 到
到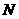 的走向为南偏东
的走向为南偏东 ,在
,在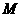 的南偏东
的南偏东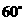 方向上有一点
方向上有一点 ,以
,以 为圆心,
为圆心, 为半径的圆形区域为居民区,取
为半径的圆形区域为居民区,取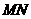 上另一点
上另一点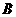 ,测得
,测得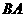 的方向为南偏东
的方向为南偏东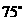 ,已知
,已知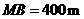 ,通过计算回答:若不改变引水方向,输水路线是否会穿过居民区?
,通过计算回答:若不改变引水方向,输水路线是否会穿过居民区?
答案:过 作
作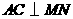 于
于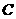 点,则
点,则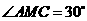 ,
, .
.
设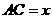 ,则
,则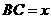 ,
, ,在Rt△
,在Rt△ 中,
中,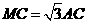 ,
,
即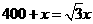 ,
,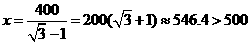 .
.
故输水线路不会穿过居民区.
第59题. 一条抛物线经过原点,请写出它的一个函数解析式
答案: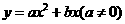
第60题. .已知抛物线的解析式为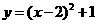 ,则抛物线的顶点坐标是( )
,则抛物线的顶点坐标是( )
A.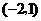 B.
B.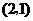 C.
C.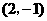 D.
D.
答案:B
第61题. 若二次函数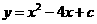 的图象与
的图象与 轴没有交点,其中
轴没有交点,其中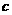 为整数,则
为整数,则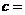 .
.
(只要求写出一个)
答案:略(答案不惟一)
第62题. 如果反比例函数 的图象如图所示,那么二次函数
的图象如图所示,那么二次函数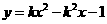 的图象大致为( )
的图象大致为( )
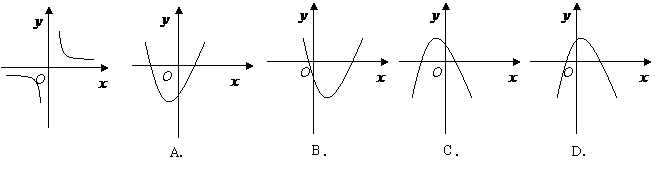
答案:B
2.结识抛物线
第1题. 二次函数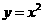 的图像是一条 ,它的开口向 ,它的对称轴为 ,它的顶点坐标为 .
的图像是一条 ,它的开口向 ,它的对称轴为 ,它的顶点坐标为 .
答案:抛物线 上  轴
轴 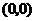
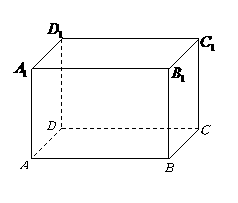 第2题. 如图,长方体
第2题. 如图,长方体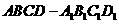 中,其三边长度比
中,其三边长度比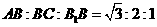 ,若
,若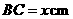 ,长方体的表面积为
,长方体的表面积为 ,则
,则 关于
关于 的函数关系式为 ,此函数的图像是一条 中
的函数关系式为 ,此函数的图像是一条 中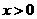 的部分,
的部分, 的值一定是随着
的值一定是随着 值的增大而 .
值的增大而 .
答案: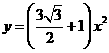 抛物线 增大
抛物线 增大
第3题. 若等腰直角三角形的斜边长为 ,其面积为
,其面积为 .
.
(1)求 关于
关于 的函数关系式,并求
的函数关系式,并求 的取值范围.
的取值范围.
(2)列出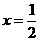 ,1,
,1,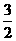 ,2,
,2, ,3时,
,3时, 与
与 的对应值表.
的对应值表.
(3)画出 关于
关于 的函数图像.
的函数图像.
答案:(1)斜边长 ,直角边长为
,直角边长为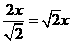 ,
,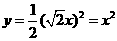 ,
,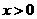 .
.
(2)

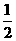
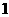
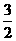
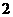

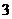

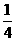
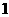
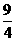
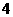
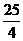
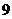
(3)图略.
第4题. 求直线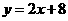 与抛物线
与抛物线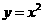 的交点
的交点 ,
,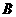 的坐标,及△
的坐标,及△ 的面积.
的面积.
答案:由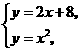 得
得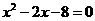 ,解之得
,解之得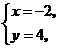
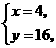
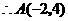 ,
,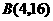 .
.
设直线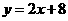 与
与 轴交于点
轴交于点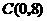 ,
,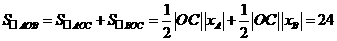 .
.
第5题. 求下列各题中直线与抛物线的两个交点的坐标.
(1)直线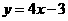 和抛物线
和抛物线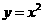 ;(2)直线
;(2)直线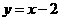 和抛物线
和抛物线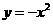 ;
;
(3)直线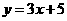 和抛物线
和抛物线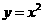 .
.
答案:(1)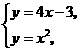
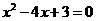 ,
,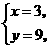
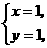
 交点
交点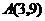 ,
,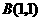 .
.
(2)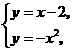
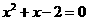 ,
,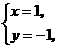
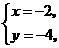
 交点
交点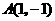 ,
,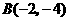 .
.
(3)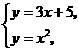
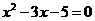 ,
,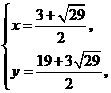
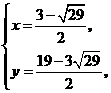
 交点
交点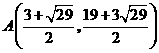 ,
,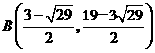 .
.
第6题. 直线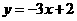 与抛物线
与抛物线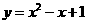 的交点坐标为 .
的交点坐标为 .
答案: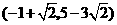 ,
,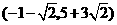
第7题. 抛物线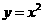 在对称轴左边,随着
在对称轴左边,随着 的增大,
的增大, 的值 ,在对称轴的右边,随着
的值 ,在对称轴的右边,随着 的增大,
的增大, 的值 .
的值 .
答案:减小,增大
第8题. 根据表格写出 与
与 的函数关系式,并作出图象.
的函数关系式,并作出图象.
 |
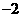 |
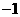 |
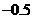 |
0 |
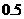 |
1 |
2 |
 |
4 |
1 |
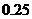 |
0 |
0.25 |
1 |
4 |
答案: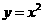 ,图略
,图略
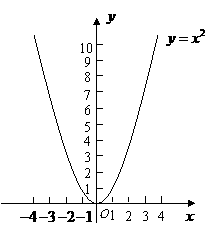 第9题. 观察二次函数
第9题. 观察二次函数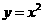 的图象,并填空.
的图象,并填空.
图像与 轴的交点也是它的 ,这个点的坐标是 .
轴的交点也是它的 ,这个点的坐标是 .
答案:顶点 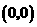
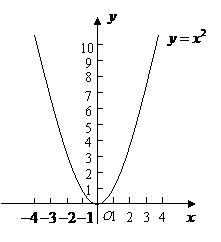 第10题. 观察二次函数
第10题. 观察二次函数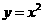 的图像,并填空.
的图像,并填空.
当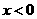 时,随着
时,随着 值的增大,
值的增大, 的值 ;当
的值 ;当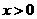 时,随着
时,随着 值的增大,
值的增大, 的值 .
的值 .
答案:减小 增大
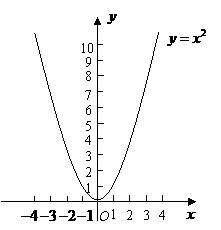 第11题. 观察二次函数
第11题. 观察二次函数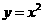 的图像,并填空.
的图像,并填空.
当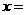 时,
时,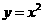 的值最小,最小值是 .
的值最小,最小值是 .
答案:0 0
第12题. 函数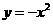 与
与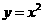 相比较,相同点是 ,不同点是 .
相比较,相同点是 ,不同点是 .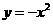 的图象与
的图象与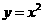 的图像的形状 ,开口方向 .在同一坐标系中,两图像关于 对称.
的图像的形状 ,开口方向 .在同一坐标系中,两图像关于 对称.
答案:都只含二次项 二次项的系数互为相反数 相同 相反  轴
轴
第13题. 对于函数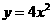 ,下列说法正确的是( )
,下列说法正确的是( )
A.当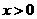 时,
时, 随
随 的增大而减小
的增大而减小
B.当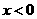 时,
时, 随
随 的增大而减小
的增大而减小
C. 随
随 的增大而减小
的增大而减小
D. 随
随 的增大而增大
的增大而增大
答案:B
第14题. 某涵洞是抛物线形,它的截面如图所示,现测得水面宽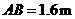 ,涵洞顶点
,涵洞顶点 到水面的距离为
到水面的距离为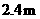 .试写出涵洞所在抛物线的函数表达式.
.试写出涵洞所在抛物线的函数表达式.

答案:由已知点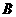 到
到 轴的距离是
轴的距离是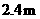 ,到
,到 轴的距离是
轴的距离是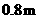 ,故
,故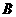 点坐标是
点坐标是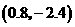 .设
.设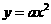 ,则
,则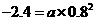 ,
,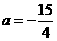 ,即
,即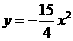 .
.
第15题. 抛物线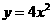 ,
,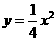 ,
,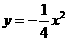 的共同特点是( )
的共同特点是( )
A.关于 轴对称,开口向上
轴对称,开口向上
B.关于 轴对称,
轴对称, 随
随 的增大而增大
的增大而增大
C.关于 轴对称,
轴对称, 随
随 的增大而减小
的增大而减小
D.关于 轴对称,顶点是原点
轴对称,顶点是原点
答案:D
第16题. 下列函数中,当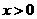 时,
时, 随
随 的增大而减小的是( )
的增大而减小的是( )
A.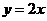 B.
B.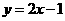 C.
C.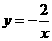 D.
D.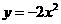
答案:D
第17题. 将二次函数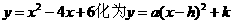 的形式:
的形式: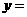 .
.
答案: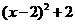 ;
;
25. 某企业投资100万元引进一条产品加工生产线,若不计维修、保养费用,预计投产后每年可创利33万.该生产线投产后, 图5
从第1年到第x年的维修、保养费用累计为y(万元),且y=ax2+bx,
若第1年的维修、保养费用为2万元,第2年为4万元。
(1)求y的解析式;
(2)投产后,这个企业在第几年就能收回投资?
24. 甲车在弯路作刹车试验,收集到的数据如下表所示:
|
速度x(千米/小时) |
0 |
5 |
10 |
15 |
20 |
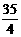 25 25 |
… |
|
刹车距离y(米) |
0 |
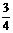 |
2 |
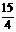 |
6 |
|
… |
(1)
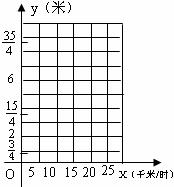 请用上表中的各对数据(x,y)作为点的坐标,
请用上表中的各对数据(x,y)作为点的坐标,
在图5所示的坐标系中画出甲车刹车距离y(米)与
(2)在一个限速为40千米/时的弯路上,甲、乙两车相向
速度x(千米/时)的函数图象,并求函数的解析式。
而行,同时刹车,但还是相撞了。事后测得甲、乙两车的
刹车距离分别为12米和10.5米,又知乙车的刹车距离y(米)
与速度x(千米/时)满足函数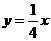 ,请你就两车的速度方面分析相撞的原因。
,请你就两车的速度方面分析相撞的原因。
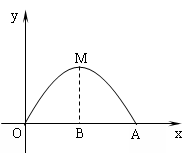
23.有一个抛物线形的桥洞,桥洞离水面的最大高度BM为3米,跨度OA为6米,以OA所在直线为x轴,O为原点建立直角坐标系(如图4所示).
⑴请你直接写出O、A、M三点的坐标;
⑵一艘小船平放着一些长3米,宽2米且厚度均匀的矩形木板,要使该小船能通过此桥洞,问这些木板最高可堆放多少米(设船身底板与水面同一平面)? 图4
22.已知抛物线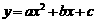 经过(-1,0),(0,-3),(2,-3)三点.
经过(-1,0),(0,-3),(2,-3)三点.
⑴求这条抛物线的表达式;
⑵写出抛物线的开口方向、对称轴和顶点坐标.
21. 已知一次函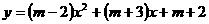 的图象过点(0,5)
⑴ 求m的值,并写出二次函数的关系式;
⑵ 求出二次函数图象的顶点坐标、对称轴.
的图象过点(0,5)
⑴ 求m的值,并写出二次函数的关系式;
⑵ 求出二次函数图象的顶点坐标、对称轴.
20.抛物线y=ax2+bx+c的图角如图3,则下列结论:①abc>0;②a+b+c=2;③a>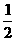 ;
;
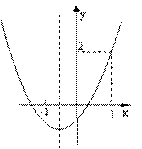 ④b<1.其中正确的结论是( )
④b<1.其中正确的结论是( )
(A)①② (B)②③ (C)②④ (D)③④
图3
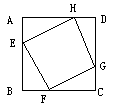
19.如图2,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,
且AE=BF=CG=DH,
设小正方形EFGH的面积为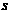 ,AE为
,AE为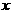 ,则
,则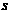 关于
关于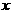 的函数图象大致是( )
的函数图象大致是( )
图2
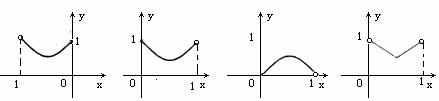
(A) (B) (C) (D)
18. 在一定条件下,若物体运动的路程s(米)与时间t(秒)的关系式为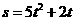 ,则当物体经过的路程是88米时,该物体所经过的时间为( )
,则当物体经过的路程是88米时,该物体所经过的时间为( )
 (A)2秒 (B) 4秒 (C)6秒 (D) 8秒
(A)2秒 (B) 4秒 (C)6秒 (D) 8秒
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com