
题目列表(包括答案和解析)
4、如图,在□ABCD中,E为BC上一点,BE∶EC=2∶3,AE交BD于点F,则BF∶FD= 。
3、已知数3、6,请再写出一个数,使这三个数中的一个数是另外两个数的比例中项,则这个数是 。
2、若 ,则
,则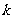 =
。
=
。
1、若 ,则
,则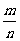 = ;若
= ;若 ,且
,且 ,则
,则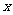 = ,
= ,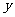 = ,
= , = 。
= 。
(二)任务要求:
(1)作图:将下面图2中的直方图补充完整;在图3中作出流量与时间的折线图.
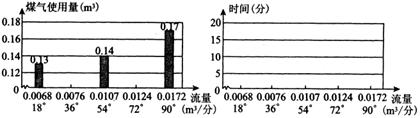
(2)填空:①从图2可以看出,烧开一壶水所耗用的最少煤气量为_______m2,此时旋钮位置在______.
②从图3可以看出,不考虑煤气用量,烧开一壶水所用的最短时间为_______分钟,此时旋钮位置在______.
(3)通过实验,请你对上述结果(用煤气烧水最省时和最省气)作一个简要的说明.
21.(本题10分)
某村王大爷家有一块梯形形状的稻田(如图所示),已知:上底AD=40米,下底BC=60米,高h=30米,王大爷准备把这块梯形形状的稻田平均分给两个儿子(面积相等)。
(1)分割方法有无数种,请你帮助王大爷设计两种不同的分割方案,在图1、图2中分别画出来,并说明理由;
(2)为了尽可能减少筑砌分割田坎的劳动量(只考虑田坎长度对工时的影响,不计其它因素),问:田坎应砌在什么位置最短?请在图3中画出来,并求出此时分割线的长度。

图1 图2 图3
22.(本题12分)如图,在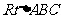 中,
中,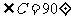 以AC为直径
以AC为直径
作圆O,交AB边于点D,过点O作OE∥AB,交BC边于点E。
(1)试判断ED与圆O位置关系,并给出证明;
(2)如果圆 O的半径为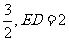 ,求AB的长.
,求AB的长. 
23.(本题12分)
某宾馆有30间房间要出租,经过一段时间的经营发展,当每间房的租金为每日200元时,恰好全部租出。在此基础上,当每间房的租金每日提高10元时,就少租出一间,已知该宾馆每日平均每间房需支出各种费用150元,设每间房每日租金为x元,该宾馆出租房间的日收益为y元。
(1)用含x的代数式表示每日未租出的房间数。
(2)求y与x之间的函数关系式。
(3)当x 为何值时,该宾馆日收益最大?最大的日收益是多少?
24.(本小题满分 14分)
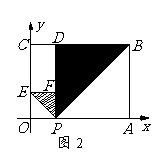
如图1,在平面直角坐标系中,有一张矩形纸片OABC,已知O(0,0),A(4,0),C(0,3),点P是OA边上的动点(与点O、A不重合).现将△PAB沿PB翻折,得到△PDB;再在OC边上选取适当的点E,将△POE沿PE翻折,得到△PFE,并使直线PD、PF重合.
(1)设P(x,0),E(0,y),求y关于x的函数关系式,并求y的最大值;
(2)如图2,若翻折后点D落在BC边上,求过点P、B、E的抛物线的函数关系式;
(3)在(2)的情况下,在该抛物线上是否存在点Q,使△PEQ是以PE为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q的坐标.



龙港三中2009年毕业生第一次模拟考试
(一)问题背景:
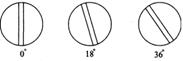
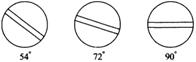
某校九年级(1)班课题学习小组对家庭煤气的使用量做了研究,其实验过程和对数据的处理如下.仔细观察现在家庭使用的电子打火煤气灶,发现当关着煤气的时候,煤气旋钮(以下简称旋钮)的位置为竖起方向,把这个位置定为0°,煤气开到最大时,位置为90°.(以0°位置作起始边,旋钮和起始边的夹角).在0~90°之间平均分成五等分,代表不同的煤气流量,它们分别是18°,36°,54°,72°,90°,见图1.
|
位置 |
烧开一壶水所需 |
流量 |
|
|
时间(分) |
煤气量(m3) |
m3/分 |
|
|
18° |
19 |
0.13 |
0.0068 |
|
36° |
16 |
0.12 |
0.0076 |
|
54° |
13 |
0.14 |
0.0107 |
|
72° |
12 |
0.15 |
0.0124 |
|
90° |
10 |
0.17 |
0.0172 |
在这些位置上分别以烧开一壶水(3.75升)为标准,记录所需的时间和所用的煤气量.并根据旋钮位置以及烧开一壶水所需时间(用t表示)、所用煤气量(用v表示),计算出不同旋钮位置所代表的煤气流量(用L表示),L=v/t,数据见右表.这样为可以研究煤气流量和烧开一壶水所需时间及用气量之间的关系了.
17.(本题10分)
(1) 计算: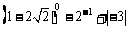
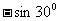 (2) 解方程:
(2) 解方程:
18.(本题8分) 如图,在□ABCD中,E,F是对角线AC上的两点,且AE=CF.
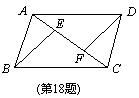 求证:BE=DF.
求证:BE=DF.
19.(本题8分)
 小敏的爸爸买了某项体育比赛的一张门票,她和哥哥两人都很想去观看.可门票只有一张,读九年级的哥哥想了一个办法,拿了8张扑克牌,将数字为2、3、5、9的四张牌给小敏,将数字为4、6、7、8的四张牌留给自己,并按如下游戏规则进行:小敏和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌数字相加,如果和为偶数,则小敏去;如果和为奇数,则哥哥去.
小敏的爸爸买了某项体育比赛的一张门票,她和哥哥两人都很想去观看.可门票只有一张,读九年级的哥哥想了一个办法,拿了8张扑克牌,将数字为2、3、5、9的四张牌给小敏,将数字为4、6、7、8的四张牌留给自己,并按如下游戏规则进行:小敏和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌数字相加,如果和为偶数,则小敏去;如果和为奇数,则哥哥去.
(1)请用画树形图或列表的方法求小敏去看比赛的概率;
(2)哥哥设计的游戏规则公平吗? 若公平,请说明理由;
若不公平,请你设计一种公平的游戏规则.
20.(本题8分)
16、 如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是_____________.
如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是_____________.
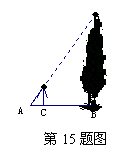
15.如图,身高为1.5m的某学生想测量一棵大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3m , CA=1m, 则树的高度为 m。


14、如图,菱形OABC中,∠A=120°,OA=1,将菱形OABC绕点O按顺时针方向旋转90°至OA′B′C′的位置,则图中由BB′,B′A′,A′C,CB围成的阴影部
分的面积是_____________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com