3、二次函数y=－x²，当x₁<x₂<0时，y₁与y₂的大小为______.

2、函数y=，当k=______时，它的图象是开口向下的抛物线；此时当x______时，y随x的增大而减小.

1、若函数y=(k²－4)x²+(k+2)x+3是二次函数，则k______.

解：设西装每件提高x元，总获得的利润为y元．则每件可获得的利润为 (20+x)元，

　　 售出件数为1000 (1－0.5%•x)，还有1000×0.5%•x件没售出

　 根据题意得：y＝(20+x)×1000 (1－0.5%•x)－1000×0．5%•x×80

　　　　　　　　 ＝－5x ²+500x+20000

　　　　　　　　 ＝－5 (x－50) ²+32500

　　　　 ∴ 当x＝50时，y有最大值32500

　　 即每件定价为150元时，获得的利润最大为32500元．

另解：y＝(100+x)×1000 (1－0．5%•x)－1000×80

　　　 ＝－5x ²+500x+20000

＝－5 (x－50) ²+32500

∴ 当x＝50时，y有最大值32500

　　 即每件定价为150元时，获得的利润最大为32500元．

⑴根据已知和结论中现有的信息，你能否求出题中的二次函数解析式？若能，请写出求解过程，并画出二次函数的图象；若不能，请说明理由．

⑵请你根据已有的信息，在原题中的矩形框中，填加一个适当的条件，把原题补充完整．

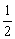解：(1)根据题意得：二次项系数　 a＝　　　　　　　　　　　　　　　　　 a＝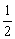

　　　　　 对称轴x＝3得：－　　　　　　　　　　　　　 解得：　　 b＝－3

　　　　 图象过点A(C，－2)得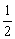：×c ²+b×c+c＝－2　　　　　　　　　 c＝2

　　　 ∴这个二次函数图象的解析式为：y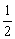＝x ²－3x+2

　 (2)　 ∵y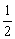＝(x ²－6x+9) 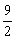－+2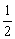＝(x－3) ²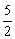－　 以下其中的一种情况(均可得分)

① 过抛物线的任意一点的坐标；

② 顶点坐标为(3，－)；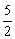

③ 当x轴的交点坐标(3+，0)或(3－，0)；

④ 当y轴的交点坐标为(0，2)

⑤ b＝－3或c＝2．

(1)如果增加x台机器，每天的生产总量为y个，请你写出y与x之间的关系式；

(2)增加多少台机器，可以使每天的生产总量最大？最大总量是多少？

解：(1)根据题意得：y＝(80+x) (384－4x)＝－4x ²+64x+30720　 (0< x < 96)

　 (2)∵y＝－4x ²+64x+30720＝－4( x ²－16x+64)+256+30720

　　　 ＝－4( x－8) ²+30976

　　　 ∴当x＝8时，y有最大值30976

　　　 则增加8台机器，可以使每天的生产总量最大，最大总量是30976台．

(1) x在什么范围内，学生的接受能力逐步增加？x在什么范围内，学生的接受能力逐步降低？

(2)第10分钟时，学生的接受能力是多少？

(3)第几分钟时，学生的接受能力最强？

解：(1)∵y＝－0.1(x²－26x+169)+16.9+43＝－0.1(x－13) ²+59.9

　　　 ∴对称轴是：直线x＝13　

　　　 即当(0≤x≤13) 提出概念至13分之间，学生的接受能力逐步增加；

　　　　 当(13≤x≤30)提出概念13分至30分之间，学生的接受能力逐步降低；

(2) 当x＝10时，y＝－0．1×10²+2.6×10+43＝59

(3) 当x＝13时，y最大59.9即第13分钟时，学生的接受能力最强．

解：根据题意设抛物线解析式为：y＝ax ²+h

　　 又知B (2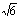，0)，D (2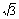，3)

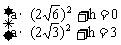　　 ∴　 解得：

　　 ∴y＝－x ²+6　　 ∴E (0，6) 即OE＝6

　 EF＝OE－OF＝3　　 t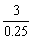＝＝＝12 (小时)

　 答：水过警戒线后12小时淹到拱桥顶．

2、根据图象写出使y₁ > y₂的x的取值范围．

解：(1)由图象可知：B (2，4)在二次函数y₂＝ax²上

　　 ∴4＝a×2²　 ∴a＝1　 则二次函数y₂＝x²

　　 又A (－1，n)在二次函数y₂＝x²上

　　　 ∴n＝(－1)²　 ∴n＝1　 则A (－1，1)

　　 又A、B两点在一次函数y₁＝kx+b上

　　 ∴　 解得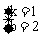：　 则一次函数y₁＝x+2

　　 ∴一次函数y₁＝x+2 ， 二次函数y₂＝x²

　 (2) 根据图象可知：当－1 < x <2时，y₁ > y₂

(1)　　 求这个函数图象的顶点坐标、对称轴以及函数的最大值；

(2)　　 若另一条抛物线y＝x²－x－k与上述抛物线只有一个公共点，求k的值．

解：(1)∵y＝－3x²－6x+5＝－3 (x²+2x+1)+8＝－3 (x+1) ²+8

∴对称轴x＝－1，顶点坐标 (－1，8)，当x＝－1时，函数有最大值是8．

　 (2) ∵只有一个公共点

　　　 ∴方程－3x²－6x+5＝x²－x－k 有相等实数根， 即4x²+5x－5－k＝0

　　 △＝5 ²－4×4×(－5－k)＝0　　 ∴k＝－

　 当x取何值时，y < 0 ? 当x取何值时，y > 0 ?

解：∵y＝－x²+2x+3＝－(x－1) ²+4　

∴开口方向向上，对称轴x＝1，顶点坐标 (1，4)

　　 令x＝0得：y＝3　 ∴与y轴交点坐标(0，3)

　　 令y＝0得：－x²+2x+3＝0　 解得：x ₁＝1 x ₂＝3

　 ∴与x轴交点坐标 (1，0) ，(3，0)　　

作出函数如图所示的图象

　 由图象说明：当x < －1或x > 3时，y < 0；当－1 < x <3时，y > 0；