9，二次函数y=－4x²+2x+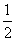的对称轴是直线__________．

10，已知点P(5，25)在抛物线y=ax²上，则当x=1时，y的值为__________．　

11，函数y=x²+2x－8与x轴的交点坐标是_________．

12，用配方法将二次函数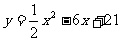化成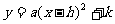的形式，那么y=_____________．

13，将y=3x²向左平移3个单位，再向下平移2个单位后，所得图像的函数表达式是_____．

14，现出二次函数y=x²+4x与y=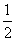－(x－3)²+2的不同点＿＿＿＿(至少现出5个)．

15，已知二次函数与x轴交点的横坐标为，则对于下列结论：

①当时，；②当时，；③方程有两个不相等的实数根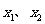；④；⑤，其中所有正确的结论是________(只需填写序号)

16，小王利用计算机设计了一个计算程序，输入和输出的数据如下表：

若输入的数据是x时，输出的数据是y，y是x的二次函数，则y与x的函数表达式为___．

1，抛物线y=(x-2)²+3的对称轴是(　 　 )

　　 A．直线x=-3　　 B．直线x=3　　 C．直线x=-2　　 D．直线x=2

　 　2，在同一坐标系中，抛物线y=4x²，y=x²，y=-x²的共同特点是( 　 )

　　 A．关于y轴对称，开口向上　　　 B．关于y轴对称，y随x的增大而增大

　　 C．关于y轴对称，y随x的增大而减小　 D．关于y轴对称，顶点是原点

3，把抛物线y=3x²先向上平移2个单位，再向右平移3个单位，所得抛物线的函数表达式为( 　 )

A．y=3(x+3)²-2　　 B．y=3(x+3)²+2　　 C．y=3(x-3)²-2　　 D．y=3(x－3)²+2

4，把抛物线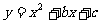的图象向右平移3个单位，再向下平移2个单位，所得图象的解析式是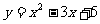，则有(　　 )

A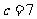，，　　　　　　　　 B，，

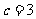C，，　　　　　　　　 D，，

5，已知函数y=ax²+bx+c的图像如图1所示，则下列关系成立且能最精确表述的是(　 )

　　 A．　　　　 B．　　　 C．　　　 D．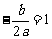

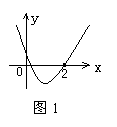
6，函数y=ax²+bx+c的图像如图2所示，那么关于x的方程ax²+bx+c-3=0的根的情况是(　 　 )

　　 A．有两个不相等的实数根　　 B．有两个异号的实数根

C．有两个相等的实数根　　　 D．没有实数根

7，当k取任意实数时，抛物线的顶点所在曲线是　 (　　 )

A．　　　　 B．　　　 C．　 D．

8，已知四点A(1，2)，B(.，0)，C(－2，20)，D(－1，12)则下列说法正确的是(　)

A．存在一个二次函数，它的图象同时经过这四个点

B．存在一个二次函数y=x²+2，它的图象同时经过这四个点

C．存在一个二次函数y=－x²－5 x +6，它的图象同时经过这四个点　

D．不存在二次函数，使得它的图象同时经过这四个点

27.(14分)来商场销售一批衬衫，平均每天可售出20件，每件盈利40元，为了扩大销售，增加盈利，尽快减少库存，商场决定取适当的降价措施，经过市场调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件. 　(1)若商场平均每天要盈利1200元，每件衬衫应降价多少元？ 　(2)每件衬衫降价多少元时，商场平均每天盈利最多？ 　28.(14分)在直角坐标平面中，O为坐标原点，二次函数y=x²+bx+c的图象与x轴的负半轴相交于点A，与x轴的正半轴相交于点B，与y轴相交于点C(如下图)，点C的坐标为(0，-3)，且BO=CO. 　(1)求这个二次函数的解析式； 　(2)设这个二次函数图象的顶点为M，求AM的长. 　

26.(12分).(2008年温州市)一次函数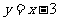的图象与轴，轴分别交于点．一个二次函数的图象经过点．

(1)求点的坐标，并画出一次函数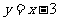的图象；

(2)求二次函数的解析式及它的最小值．

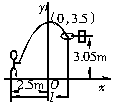　13.二次函数y=x²+kx+m的顶点坐标是(1，-3)，则k=　　，m=＿＿＿. 　14.已知二次函数y=x²+(m+3)x+m的图象关于y轴对称，则m的值是　　，它与x轴的交点坐标是　. 　15.已知二次函数y=x²+3x+k与x轴的两个交点在原点的右侧，则k的取值范围是　　. 　16.已知抛物线y=ax²+bx+c经过点A(-2，7)，B(6，7)，C(3，-8)，则该抛物线上纵坐标为-8的另一点的坐标是　　. 　17.已知函数①y=x²+2；②y=-3x²+x，函数　　(填序号)有最小值，当x=＿＿＿时该函数的最小值是　　. 　18.二次函数y=-x²+2x+3的图象与x轴交点为A、B，P为它的顶点，则S_△PAB=　　　 . 　19.抛物线y=ax²+bx+c与x轴的交点是(-3，0)，(-5，0)，则这条抛物线的对称轴是直线　　. 　20. 将抛物线y=-x²+1向右平移2个单位，再向下平移3个单位，所得到的抛物线解析式为＿＿＿对于平移后的抛物线，当　　时，y随x的增大而减小；当x=　　时，函数有最　　值为　　 . 　21.将二次函数y=-3x²+6x-1配成y=a(x-h)²+k的形式为　　. 　22.已知函数y=x²-x-2，当＿＿＿＿时，函数值y<0. 　三专心解一解(共74分)

23.(10分)若二次函数y=ax²+bx+c的图象的顶点坐标为(2，-1)，且抛物线过(0，3)，求二次函数的解析式. 　24.(12分)对于抛物线，在不计空气阻力的情况下，有如下关系式：h=V₀t－gt²，h(米)是上升高度，V₀(米/秒)是物体的初速度，g(米/秒²)是重力加速度，t(秒)是物体抛出后经过的时间，如下图是h与t的函数关系图象. 　(1)求V₀，g； 　(2)几秒后，物体在离开抛物点25米高的地方？ 　 　25.(12分)如图，有长为24米的篱笆，一面利用墙(墙的最大可用长度a为10米)，围成中间隔有一道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S米². 　(1)求S与x的函数关系式； 　(2)如果要围成面积为45m²的花圃，AB的长是多少米？ 　(3)能围成面积比45m²更大的花圃吗？如果能，请求出最大面积，并说明围法；如果不能，请说明理由. 　

5.为解决药价高给老百姓带来的求医难的问题，国家决定对某药品分两次降价，若设平均每次降价的百分率是x，该药品的原价是m元，降价后的价格是y元，则y与x之间的函数关系式是(　). 　A.y=2m(1-x)　　B.y=2m(1+x) 　C.y=m(1-x)²　　D.y=m(1+x)² 　6.如图，抛物线y=ax²+bx+c(a≠0)的图象与x轴的一个交点是(-2，0)，顶点是(1，3)，下列说法不正确的是　　　　　　　　　　　　　　　(　). 　A.抛物线的对称轴是直线x=1 　B.抛物线的开口向下 　C.抛物线与x轴的另一个交点为(2，0) 　D.当x=1时，y有最大值是3 　7.将抛物线y=x²-2x+1向下平移2个单位，再向右平移1个单位，所得的抛物线为(　). 　A.y=x²-2x-1　　B.y=x²+2x-1 　C.y=x²-4x+2　　D.y=x²+2 　8.二次函数y=x²+mx+n，若m-n=0，则它的图象必过点　　　(　). 　A.(-1，1)　　B.(1，-1) 　C.(-1，-1)　　D. (1，1) 　9.二次函数y=ax²+bx+c中，若b²=ac，且x=0时，y=-4，则　　(　). 　A. y_最大=-4　　B. y_最小=-4 　C. y_最大=-3　　　D. y_最小=-3 　10.已知，二次函数y=ax²+bx+c，如果a>b>c，且a+b+c=0，则它的图象可能是下图中的(　). 　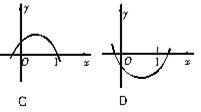 　11.已知抛物线y=ax²+bx+c如图所示，则关于x的方程ax²+bx+c-3=0的根的情况是(　). 　 　A. 有两个不相等的正实根 　B. 有两个异号实根 　C. 有两个相等的实根 　D. 没有实数根 　12.小敏在某次投篮中，球的运动路线是抛物线y=－x²+3.5的一部分(如图)，若命中篮圈中心，则他与篮底的距离l是　　　　　　　　　　(　). 　A.3.5m 　B.4m 　C.4.5m 　D.4.6m 　

第Ⅱ卷(非选择题部分，共114分)

　1.在抛物线y=x²-3x-1上的点是　　　　　　　(　) 　A.(1，2)　B.(1，3)　C.(-2，-8)　D.(－) 　2. (2008福建福州)已知抛物线与轴的一个交点为，

则代数式的值为(　　 )

A．2006　　　　 B．2007　　　　 C．2008　　　　 D．2009

3.已知二次函数y=ax²+bx+c的图象开口向下，顶点在第二象限，则(　). 　A.a<0，b<0　　B.a>0，b²-4ac>0 　C.a<0，b>0　　D.a<0，b²-4ac<0 　4. (08四川省资阳市)在平面直角坐标系中，如果抛物线y＝2x²不动，而把x轴、y轴分别向上、向右平移2个单位，那么在新坐标系下抛物线的解析式是

A．y＝2(x－2)² + 2　　　　　　　　　　　　　　　　　 　　　　　　　 B．y＝2(x + 2)²－2

C．y＝2(x－2)²－2　　　　　　　　　　　　　　　　　 　　　　　　　 D．y＝2(x + 2)² + 2

18、a=2　 h=-4

17、略

16、