
题目列表(包括答案和解析)
9.二次函数y=- 2x2+3的开口方向是_________.
2x2+3的开口方向是_________.
8.关于二次函数y=x2+4x-7的最大(小)值,叙述正确的是( )
A.当x=2时,函数有最大值 B.x=2时,函数有最小值
C.当x=-1时,函数有最大值 D.当x=-2时,函数有最小值
7.已知二次函数y=- x2-3x-
x2-3x- ,设自变量的值分别为x1,x2,x3,且-3<x1<x2<x3, 则对应的函数值y1,y2,y3的大小关系是( )
,设自变量的值分别为x1,x2,x3,且-3<x1<x2<x3, 则对应的函数值y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y1<y2<y3 C.y2>y3>y1 D.y2<y3<y1
6.已知h关于t的函数关系式为h= gt2(g为正常数,t为时间), 则如图2中函数的图像为( )
gt2(g为正常数,t为时间), 则如图2中函数的图像为( )

5.如果二次函数 (a>0)的顶点在x轴上方,那么( )
(a>0)的顶点在x轴上方,那么( )
A.b2-4ac≥0 B.b2-4ac<0 C.b2-4ac>0 D.b2-4ac=0
4. 二次函数
二次函数 的图象如图1所示,则下列结论正确的是( )
的图象如图1所示,则下列结论正确的是( )
A. B.
B.
C.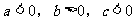 D.
D.
3.若y=(2-m)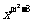 是二次函数,且开口向上,则m的值为( )
是二次函数,且开口向上,则m的值为( )
A. B.-
B.-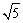 C.
C.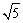 D.0
D.0
2.抛物线y=x2+2x-2的图象最高点的坐标是( )
A.(2,-2) B.(1,-2) C.(1,-3) D.(-1,-3)
1.已知点(a,8)在二次函数y=a x2的图象上,则a的值是( )
A.2 B.-2 C.±2 D.±
17,利用二次函数的图像求下列一元二次方程的近似根.
(1)x2-2x-1=0; (2)x2+5=4x.
 18,汽车行驶中,由于惯性作用,刹车后还要向前滑行一段距离才能停止,我们称这段距离为“刹车距离”,刹车距离是分析交通事故的一个重要因素.在一个限速40千米/时以内的弯道上,甲、乙两车相向而行,发现情况不对,同时刹车,但还是相碰了.事后现场测得甲车的刹车距离为12米,乙车的刹车距离超过10米, 但小于12米.查有关资料知:甲车的刹车距离
18,汽车行驶中,由于惯性作用,刹车后还要向前滑行一段距离才能停止,我们称这段距离为“刹车距离”,刹车距离是分析交通事故的一个重要因素.在一个限速40千米/时以内的弯道上,甲、乙两车相向而行,发现情况不对,同时刹车,但还是相碰了.事后现场测得甲车的刹车距离为12米,乙车的刹车距离超过10米, 但小于12米.查有关资料知:甲车的刹车距离 (米)与车速x(千米/时)之间有下列关系:
(米)与车速x(千米/时)之间有下列关系: =0.1x+0.01x2;乙车的刹车距离
=0.1x+0.01x2;乙车的刹车距离 (米)与车速x(千米/时)的关系如图3所示.请你从两车的速度方面分析相碰的原因.
(米)与车速x(千米/时)的关系如图3所示.请你从两车的速度方面分析相碰的原因.
19,某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰好在水面中心,安装在柱子顶端A处的喷头向外喷水, 水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,抛物线的形状如图4(1)和(2)所示,建立直角坐标系,水流喷出的高度y(米)与水平距离x(米)之间的关系式是y=-x2+2x+ ,请回答下列问题.
,请回答下列问题.
(1)柱子OA的高度为多少米?
(2)喷出的水流距水平面的最大高度是多少?
 (3)若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外.
(3)若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外.

20,已知抛物线y=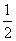 x2- x +k与
x2- x +k与 轴有两个交点.
轴有两个交点.
(1)求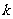 的取值范围;
的取值范围;
(2)设抛物线与x轴交于A、B两点,且点A在点B的左侧,点D是抛物线的顶点,如果△ABD是等腰直角三角形,求抛物线的解析式;
(3)在(2)的条件下,抛物线与y轴交于点C,点E在y轴的正半轴上,且以A、O、E为顶点的三角形和以B、O、C为顶点的三角形相似,求点E的坐标.
21,某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程.下面的二次函数图象(部分)刻画了该公司年初以来累积利润S(万元)与销售时间t(月)之间的关系(即前t个月的利润总和S与t之间的关系).
根据图象提供的信息,解答下列问题:
(1)由已知图象上的三点坐标,求累积利润S(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求第8个月公司所获利润是多少万元?
22,如图6,已知抛物线 与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
(1)求抛物线的解析式.
 (2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方),DE=
(2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方),DE=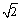 ,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com