
题目列表(包括答案和解析)
20、如果设二次函数的解析式为y=ax2+bx+c,因为图象开口向下,所以a为负数,图象过原点,即c=0,满足这两个条件的解析式有无数个. 解:y=-x2+3x.
19、解:∵点(1,0),(-5,0)是抛物线与x的两交点,
∴ 抛物线对称轴为直线x=-2,
∴ 抛物线的顶点坐标为(-2, ),
设抛物线的解析式为y=ax2+bx+c,则有
),
设抛物线的解析式为y=ax2+bx+c,则有
 ∴ 所求二次函数解析式为
∴ 所求二次函数解析式为
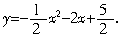
17、正确的序号为①②③④.
从图象中易知a>0,b<0,c<0,③正确;抛物线顶点纵坐标为-1,∴ ①对;当x=-1时y=a-b+c,由图象知(-1,a-b+c)在第二象限,∴ a-b+c>0,④正确;设C(0,c),则OC=|c|,∵ OA=OC=|c|,∴ A(c,0)代入抛物线得ac2+bc+c=0,又c≠0,∴ac+b+1=0,故②正确.
18、这是一道没给图象的题,由已知条件可以大致画出如下图所示的图象,∵ 0<x1<1, ∴ 点(1,a+b+c)在第一象限,又对称轴为直线x=-1,∴ (-3,9a-3b+c)在第二象限,故①9a-3b+c>0正确;∵- =-1, ∴ b=2a,∴ b-a=2a-a=a>0.∴ b>a>c,故②不正确;把b=2a代入a+b+c>0得3a+c>0, ∴ ③正确;故答案为2个.
=-1, ∴ b=2a,∴ b-a=2a-a=a>0.∴ b>a>c,故②不正确;把b=2a代入a+b+c>0得3a+c>0, ∴ ③正确;故答案为2个.

16、(1)y=x2+x; (2)纯收益g=33x-150-(x2+x)
=-x2+32x-150 (3)g=-x2+32x-150=-(x-16)2+106,即设施开放16个月后游乐场的纯收益达到最大. 又在0<x≤16时,g随x的增大而增大,当x≤5时,g<0;而当x=6时,g>0,所以6个月后能收回投资.
15、解:(1)①,④; (2)②,③,④.
14、若函数 是二次函数,则
是二次函数,则
 .解得
.解得  ,且
,且 .
.
因此,当 ,且
,且 时,函数
时,函数 是二次函数.
是二次函数.
13、 设今年投资额为2(1+x)元,明年投资为2(1+x)2元
∴由题意可得.y=2(1+x)+2(1+x)2=2x2+6x+4
12、由图像的对称轴和函数的最大值,可知顶点坐标是(3,0),设y=a(x-3)2,
把x=0,y=-1代入,得9a=-1
,a=- ,∴y=-
,∴y=- (x-3)2
(x-3)2
10、D;本题考查的是抛物线的平移.先画出y=x2的草图,图象向右平移3个单位对称轴为x=3,选项D中的二次函数的对称轴为x=3.
二、11、函数关系式是 ,即
,即
9、C. 对于任意实数m都是二次函数
对于任意实数m都是二次函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com