
题目列表(包括答案和解析)
6.如图1,已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(x1,0),B(x2,0),且x1+x2=4,  .
.
(1)求抛物线的代数表达式;
(2)设抛物线与y轴交于C点,求直线BC的表达式;
(3)求△ABC的面积.
5.利用二次函数的图像求下列一元二次方程的根.
(1)4x2-8x+1=0; (2)x2-2x-5=0;(3)2x2-6x+3=0; (4)x2-x-1=0.
4.当一枚火箭被竖直向上发射时,它的高度h(m)与时间t(s)的关系可以用h= -5t2+150t+10表示,经过___秒时,火箭到达它的最高点,此时的最高点的高度是___.
3.一个三角形的底边和这边上的高的和为10,这个三角形的面积最大可以达到___.
2.已知二次函数 的图象与x轴交于两个不同的点,则关于x的的一元二次方程
的图象与x轴交于两个不同的点,则关于x的的一元二次方程 =0的根的情况是( )
=0的根的情况是( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.没有实数根 D.无法确定
1.已知 a<-1,点(a-1, ),(a,
),(a, ),(a+1,
),(a+1, )都在函数
)都在函数 的图象上,则( )
A.
的图象上,则( )
A. <
< <
< B.
B. <
< <
< C.
C. <
< <
< D.
D. <
< <
<
25、解:(1)由题意得点E(1,1.4), B(6,0.9), 代入y=ax2+bx+0.9得

解得 
∴所求的抛物线的解析式是y=-0.1x2+0.6x+0.9.
(2)把x=3代入y=-0.1x2+0.6x+0.9得
y=-0.1×32+0.6×3+0.9=1.8
∴小华的身高是1.8米
(3)1<t<5
24、分析:商场的利润是由每件商品的利润乘每天的销售的数量所决定。
在这个问题中,每件服装的利润为(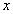
 ),而销售的件数是(
),而销售的件数是( +204),那么就能得到一个
+204),那么就能得到一个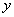 与
与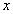 之间的函数关系,这个函数是二次函数.
之间的函数关系,这个函数是二次函数.
要求销售的最大利润,就是要求这个二次函数的最大值.
解:(1)由题意,销售利润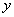 与每件的销售价
与每件的销售价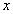 之间的函数关系为
之间的函数关系为
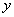 =(
=(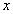 -42)(-3
-42)(-3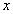 +204),即
+204),即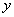 =-3
=-3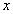 2+
2+ 8568
8568
(2)配方,得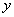 =-3(
=-3(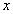 -55)2+507
-55)2+507
∴当每件的销售价为55元时,可取得最大利润,每天最大销售利润为507元.
23、解:本题不便求出方程2x2-x-8=0的根,设这个方程的根为x1、x2,则当
x=x1,x=x2时,y=4,可设y=a(2x2-x-8)+4
把x=2,y=-4代入,得-4=a(2×22-2-8 )+4得a=4,所求函数为
y=4(2x2-x-8)+4=8x2-4x-28
解:(1)列表:在x的取值范围内列出函数对应值表;
|
x |
… |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
… |
|
y |
… |
-6 |
-4 |
-2 |
-2 |
-2 |
-4 |
-6 |
… |
(2)描点:用表格里各组对应值作为点的坐标,在平面直角坐标系中描点.
(3)连线:用光滑的曲线顺次连接各点,得到函数y=-x2+x-的图象.
说明:(1)列表时,应根据对称轴是x=1,以1为中心,对称地选取自变量的值,求出相应的函数值。相应的函数值是相等的.
(2)直角坐标系中x轴、y轴的长度单位可以任意定,且允许x轴、y轴选取的长度单位不同。所以要根据具体问题,选取适当的长度单位,使画出的图象美观.
则可得到这个函数的性质如下:
当x<1时,函数值y随x的增大而增大;当x>1时,函数值y随x的增大而减小;
当x=1时,函数取得最大值,最大值y=-2.
22、 解:(1)配方,y=- (x2-4x+4-4)+2
(x2-4x+4-4)+2
=- (x-2)2+3
(x-2)2+3
∴图像的对称轴是直线x=2,顶点坐标为(2,3)。
(2)把这个函数的图像向左、向下平移2个单位,顶点成为(0,1),形状不变,得到函数y=- x+1的图像。
x+1的图像。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com