
题目列表(包括答案和解析)
(六)求值:(每小题7分,共14分)
27.已知x=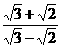 ,y=
,y=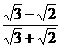 ,求
,求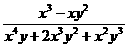 的值.
的值.
[提示]先将已知条件化简,再将分式化简最后将已知条件代入求值.
[解]∵ x=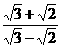 =
=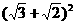 =5+2
=5+2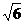 ,
,
y=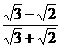 =
=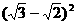 =5-2
=5-2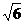 .
.
∴ x+y=10,x-y=4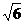 ,xy=52-(2
,xy=52-(2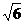 )2=1.
)2=1.
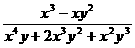 =
=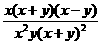 =
=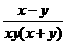 =
=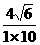 =
=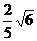 .
.
[点评]本题将x、y化简后,根据解题的需要,先分别求出“x+y”、“x-y”、“xy”.从而使求值的过程更简捷.
28.当x=1-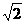 时,求
时,求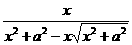 +
+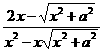 +
+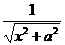 的值.
的值.
[提示]注意:x2+a2=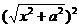 ,
,
∴ x2+a2-x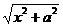 =
=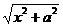 (
(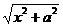 -x),x2-x
-x),x2-x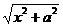 =-x(
=-x(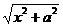 -x).
-x).
[解]原式=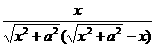 -
-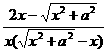 +
+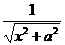
=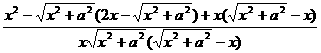
=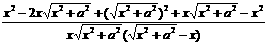 =
=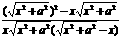 =
=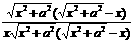
=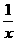 .当x=1-
.当x=1-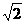 时,原式=
时,原式=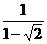 =-1-
=-1-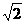 .[点评]本题如果将前两个“分式”分拆成两个“分式”之差,那么化简会更简便.即原式=
.[点评]本题如果将前两个“分式”分拆成两个“分式”之差,那么化简会更简便.即原式=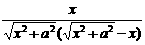 -
-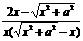 +
+
=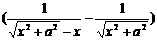 -
-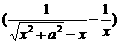 +
+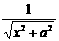 =
=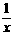 .
.
(五)计算题:(每小题6分,共24分)
23.(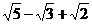 )(
)(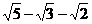 );
);
[提示]将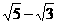 看成一个整体,先用平方差公式,再用完全平方公式.
看成一个整体,先用平方差公式,再用完全平方公式.
[解]原式=(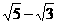 )2-
)2-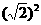 =5-2
=5-2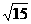 +3-2=6-2
+3-2=6-2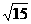 .
.
24.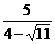 -
-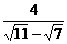 -
-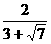 ;[提示]先分别分母有理化,再合并同类二次根式.
;[提示]先分别分母有理化,再合并同类二次根式.
[解]原式=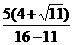 -
-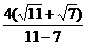 -
- =4+
=4+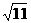 -
-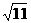 -
-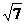 -3+
-3+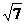 =1.
=1.
25.(a2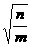 -
-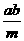
 +
+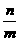
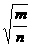 )÷a2b2
)÷a2b2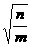 ;
;
[提示]先将除法转化为乘法,再用乘法分配律展开,最后合并同类二次根式.
[解]原式=(a2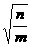 -
-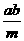
 +
+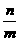
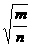 )·
)·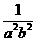
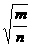
=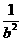
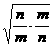 -
-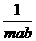
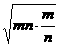 +
+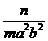
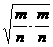
=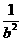 -
-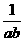 +
+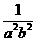 =
=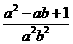 .
.
26.(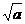 +
+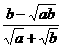 )÷(
)÷(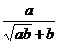 +
+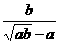 -
-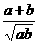 )(a≠b).
)(a≠b).
[提示]本题应先将两个括号内的分式分别通分,然后分解因式并约分.
[解]原式=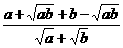 ÷
÷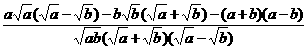
=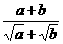 ÷
÷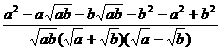
=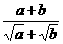 ·
·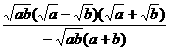 =-
=-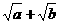 .
.
[点评]本题如果先分母有理化,那么计算较烦琐.
(四)在实数范围内因式分解:(每小题3分,共6分)
21.9x2-5y2;[提示]用平方差公式分解,并注意到5y2=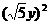 .[答案](3x+
.[答案](3x+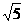 y)(3x-
y)(3x-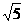 y).
y).
22.4x4-4x2+1.[提示]先用完全平方公式,再用平方差公式分解.[答案](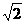 x+1)2(
x+1)2(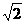 x-1)2.
x-1)2.
(三)选择题:(每小题3分,共15分)
16.已知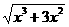 =-x
=-x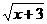 ,则………………( )
,则………………( )
(A)x≤0 (B)x≤-3 (C)x≥-3 (D)-3≤x≤0[答案]D.
[点评]本题考查积的算术平方根性质成立的条件,(A)、(C)不正确是因为只考虑了其中一个算术平方根的意义.
17.若x<y<0,则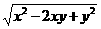 +
+ =………………………( )
=………………………( )
(A)2x (B)2y (C)-2x (D)-2y
[提示]∵ x<y<0,∴ x-y<0,x+y<0.
∴ 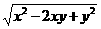 =
=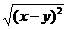 =|x-y|=y-x.
=|x-y|=y-x.
 =
=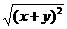 =|x+y|=-x-y.[答案]C.
=|x+y|=-x-y.[答案]C.
[点评]本题考查二次根式的性质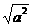 =|a|.
=|a|.
18.若0<x<1,则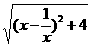 -
-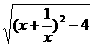 等于………………………( )
等于………………………( )
(A)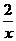 (B)-
(B)-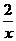 (C)-2x (D)2x
(C)-2x (D)2x
[提示](x-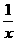 )2+4=(x+
)2+4=(x+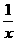 )2,(x+
)2,(x+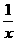 )2-4=(x-
)2-4=(x-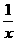 )2.又∵ 0<x<1,
)2.又∵ 0<x<1,
∴ x+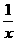 >0,x-
>0,x-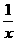 <0.[答案]D.
<0.[答案]D.
[点评]本题考查完全平方公式和二次根式的性质.(A)不正确是因为用性质时没有注意当0<x<1时,x-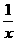 <0.
<0.
19.化简
 a<0
a<0 得………………………………………………………………( )
得………………………………………………………………( )
(A) (B)-
(B)-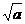 (C)-
(C)- (D)
(D)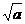
[提示]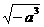 =
=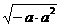 =
= ·
·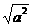 =|a|
=|a| =-a
=-a .[答案]C.
.[答案]C.
20.当a<0,b<0时,-a+2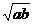 -b可变形为………………………………………( )
-b可变形为………………………………………( )
(A)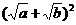 (B)-
(B)-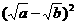 (C)
(C)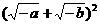 (D)
(D)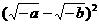
[提示]∵ a<0,b<0,
∴ -a>0,-b>0.并且-a=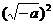 ,-b=
,-b= ,
,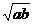 =
=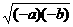 .
.
[答案]C.[点评]本题考查逆向运用公式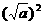 =a(a≥0)和完全平方公式.注意(A)、(B)不正确是因为a<0,b<0时,
=a(a≥0)和完全平方公式.注意(A)、(B)不正确是因为a<0,b<0时,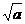 、
、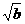 都没有意义.
都没有意义.
(二)填空题:(每小题2分,共20分)
6.当x__________时,式子 有意义.[提示]
有意义.[提示]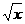 何时有意义?x≥0.分式何时有意义?分母不等于零.[答案]x≥0且x≠9.
何时有意义?x≥0.分式何时有意义?分母不等于零.[答案]x≥0且x≠9.
7.化简-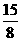
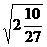 ÷
÷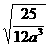 =_.[答案]-2a
=_.[答案]-2a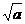 .[点评]注意除法法则和积的算术平方根性质的运用.
.[点评]注意除法法则和积的算术平方根性质的运用.
8.a-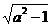 的有理化因式是____________.[提示](a-
的有理化因式是____________.[提示](a-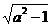 )(________)=a2-
)(________)=a2-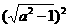 .a+
.a+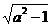 .[答案]a+
.[答案]a+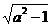 .
.
9.当1<x<4时,|x-4|+ =________________.
=________________.
[提示]x2-2x+1=( )2,x-1.当1<x<4时,x-4,x-1是正数还是负数?
x-4是负数,x-1是正数.[答案]3.
10.方程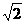 (x-1)=x+1的解是____________.[提示]把方程整理成ax=b的形式后,a、b分别是多少?
(x-1)=x+1的解是____________.[提示]把方程整理成ax=b的形式后,a、b分别是多少?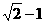 ,
,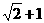 .[答案]x=3+2
.[答案]x=3+2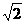 .
.
11.已知a、b、c为正数,d为负数,化简 =______.[提示]
=______.[提示]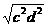 =|cd|=-cd.
=|cd|=-cd.
[答案]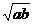 +cd.[点评]∵ ab=
+cd.[点评]∵ ab=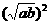 (ab>0),∴ ab-c2d2=(
(ab>0),∴ ab-c2d2=(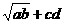 )(
)(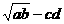 ).
).
12.比较大小:-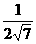 _________-
_________-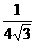 .[提示]2
.[提示]2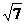 =
=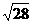 ,4
,4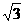 =
=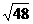 .
.
[答案]<.[点评]先比较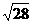 ,
,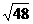 的大小,再比较
的大小,再比较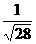 ,
,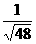 的大小,最后比较-
的大小,最后比较-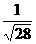 与-
与-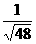 的大小.
的大小.
13.化简:(7-5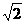 )2000·(-7-5
)2000·(-7-5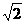 )2001=______________.
)2001=______________.
[提示](-7-5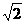 )2001=(-7-5
)2001=(-7-5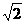 )2000·(_________)[-7-5
)2000·(_________)[-7-5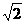 .]
.]
(7-5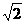 )·(-7-5
)·(-7-5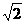 )=?[1.][答案]-7-5
)=?[1.][答案]-7-5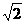 .
.
[点评]注意在化简过程中运用幂的运算法则和平方差公式.
14.若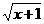 +
+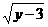 =0,则(x-1)2+(y+3)2=____________.[答案]40.
=0,则(x-1)2+(y+3)2=____________.[答案]40.
[点评]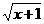 ≥0,
≥0,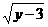 ≥0.当
≥0.当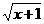 +
+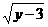 =0时,x+1=0,y-3=0.
=0时,x+1=0,y-3=0.
15.x,y分别为8-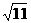 的整数部分和小数部分,则2xy-y2=____________.
的整数部分和小数部分,则2xy-y2=____________.
[提示]∵ 3<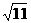 <4,∴ _______<8-
<4,∴ _______<8-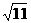 <__________.[4,5].由于8-
<__________.[4,5].由于8-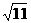 介于4与5之间,则其整数部分x=?小数部分y=?[x=4,y=4-
介于4与5之间,则其整数部分x=?小数部分y=?[x=4,y=4-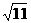 ][答案]5.
][答案]5.
[点评]求二次根式的整数部分和小数部分时,先要对无理数进行估算.在明确了二次根式的取值范围后,其整数部分和小数部分就不难确定了.
(一)判断题:(每小题1分,共5分)
1.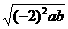 =-2
=-2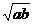 .…………………( )
.…………………( )
[提示]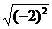 =|-2|=2.[答案]×.
=|-2|=2.[答案]×.
2.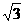 -2的倒数是
-2的倒数是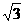 +2.( )
+2.( )
[提示]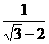 =
=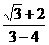 =-(
=-(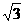 +2).[答案]×.
+2).[答案]×.
3.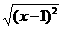 =
=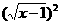 .…( )[提示]
.…( )[提示]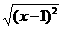 =|x-1|,
=|x-1|,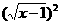 =x-1(x≥1).两式相等,必须x≥1.但等式左边x可取任何数.[答案]×.
=x-1(x≥1).两式相等,必须x≥1.但等式左边x可取任何数.[答案]×.
4.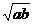 、
、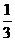
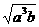 、
、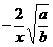 是同类二次根式.…( )
是同类二次根式.…( )
[提示]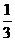
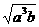 、
、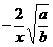 化成最简二次根式后再判断.[答案]√.
化成最简二次根式后再判断.[答案]√.
5.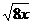 ,
,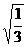 ,
,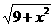 都不是最简二次根式.( )
都不是最简二次根式.( )
[答案]×.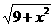 是最简二次根式.
是最简二次根式.
28.当x=1-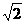 时,求
时,求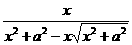 +
+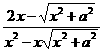 +
+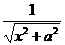 的值.
的值.
29.计算(2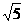 +1)(
+1)(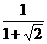 +
+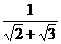 +
+ +…+
+…+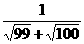 ).
).
30.若x,y为实数,且y=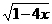 +
+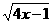 +
+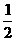 .求
.求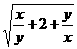 -
-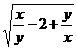 的值.
的值.
《二次根式》提高测试 答案
21.1二次根式
第1题. 函数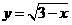 中,自变量
中,自变量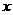 的取值范围是 .
的取值范围是 .
答案: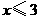 .
.
第2题. 实数a在数轴上的位置如图所示,化简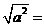 .
.

答案: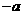 .
.
第3题. 若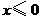 ,则化简
,则化简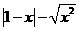 的结果是( )
的结果是( )
A.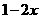 B.
B.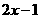 C.
C.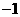 D.
D.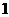
答案:D.
第4题. 函数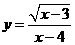 中,自变量
中,自变量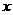 的取值范围是 .
的取值范围是 .
答案: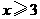 且
且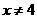 .
.
第5题. 如果等式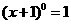 和
和 同时成立,那么需要的条件是( )
同时成立,那么需要的条件是( )
A.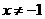 B.
B.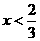 且
且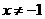
C.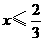 或
或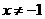 D.
D.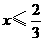 且
且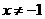
答案:D.
第6题. 化简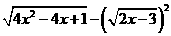 得( )
得( )
A.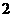 B.
B.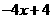 C.
C.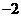 D.
D.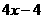
答案:A.
第7题. 当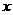 _____时,
_____时,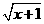 是二次根式;当
是二次根式;当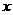 _____时,
_____时,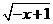 是二次根式.
是二次根式.
答案: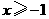 ;
;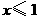 .
.
第8题. 当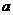 ______时,
______时,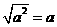 ;当
;当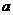 ________时,
________时,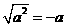 .
.
答案: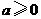 ;
;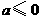 .
.
第9题. 要使下列式子有意义,字母的取值必须满足什么条件.
(1)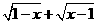 (2)
(2)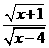
答案:(1)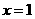 ; (2)
; (2)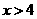 .
.
第10题. 已知实数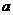 满足
满足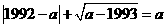 ,试求
,试求 的值.
的值.
答案: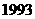 .
.
第11题. 函数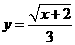 中,自变量
中,自变量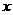 的取值范围是 .
的取值范围是 .
答案: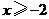 .
.
第12题. 已知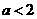 ,则
,则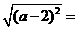 .
.
答案: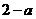 .
.
第13题. 函数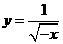 自变量的取值范围是( )
自变量的取值范围是( )
A.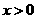 B.
B.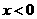 C.
C.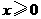 D.
D.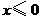
答案:B.
第14题. 在函数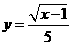 中,自变量
中,自变量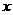 的取值范围是 .
的取值范围是 .
答案: .
.
第15题.  实数
实数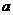 在数轴上的位置如图所示,则化简
在数轴上的位置如图所示,则化简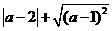 的结果为 .
的结果为 .
答案: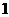 .
.
第16题. 函数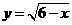 中,自变量
中,自变量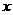 的取值范围是 .
的取值范围是 .
答案: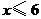 .
.
第17题. 下列说法正确的是( )
A.若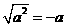 ,则
,则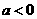 B.
B.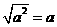 ,则
,则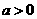
C.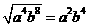 D.
D.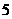 的平方根是
的平方根是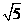
答案:C.
第18题. 函数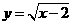 中自变量
中自变量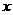 的取值范围是 .
的取值范围是 .
答案: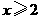 .
.
第19题. 已知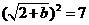 ,则
,则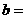 _________.
_________.
答案: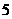 .
.
第20题. 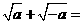 ________.
________.
答案: .
.
第21题. 当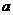 _______时,式子
_______时,式子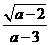 有意义.
有意义.
答案: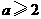 且
且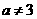 .
.
第22题. 若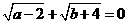 ,则
,则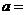 ______,
______,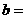 ________.
________.
答案: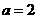 ,
,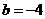 .
.
第23题. 已知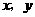 为实数,且
为实数,且 ,则
,则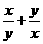 的值为________.
的值为________.
答案: .
.
第24题. 若二次根式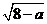 有意义,则它的最小值是( )
有意义,则它的最小值是( )
A.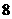 B.
B.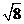 C.
C.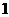 D.
D.
答案:D.
第25题. 下列各式中不成立的是( )
A.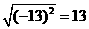 B.
B.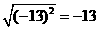
C. D.
D.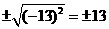
答案:B.
第26题. 应用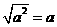
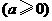 化简
化简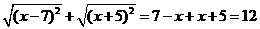 时,
时,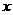 的取值范围是( )
的取值范围是( )
A.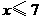 B.
B.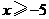 C.
C. 或
或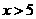 D.
D.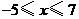
答案:D.
第27题. 如果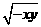 和
和 都是二次根式
都是二次根式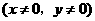 ,那么
,那么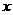 和
和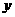 应为( )
应为( )
A.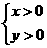 B.
B.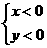 C.
C.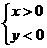 D.
D.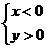
答案:C.
第28题. 若代数式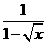 在实数范围内有意义,则
在实数范围内有意义,则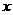 的取值范围为( )
的取值范围为( )
A.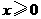 B.
B. C.
C.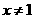 D.
D.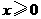 且
且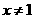
答案:D.
第29题. 若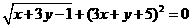 ,求
,求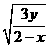 的值.
的值.
答案: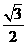 .
.
第30题. 计算:
(1)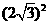 (2)
(2)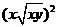 (3)
(3)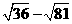
答案:(1) 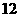 (2)
(2)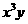 (3)
(3)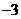
第31题. 已知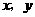 为实数,且
为实数,且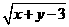 与
与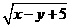 互为相反数,求
互为相反数,求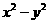 的值.
的值.
答案: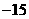 .
.
第32题. 当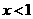 时,化简
时,化简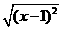 等于( )
等于( )
A.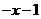 B.
B.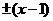 C.
C. D.
D.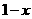
答案:D.
第33题. 若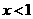 ,则
,则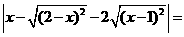 ( )
( )
A. B.
B.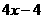 C.
C.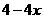 D.
D.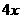
答案:C.
第34题. 若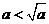 ,则
,则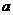 的范围是( )
的范围是( )
A.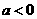 B.
B.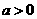 C.
C. D.
D.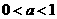
答案:D.
第35题. 若 为
为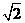 的小数部分,则
的小数部分,则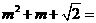 .
.
答案: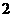 .
.
第36题. 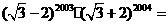 .
.
答案: .
.
第37题. 当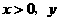 时,
时,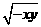 在实数范围内有意义.
在实数范围内有意义.
答案: .
.
第38题. 函数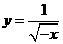 自变量的取值范围是( )
自变量的取值范围是( )
A.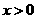 B.
B.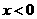 C.
C.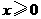 D.
D.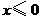
答案:B.
第39题. 若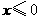 ,则化简
,则化简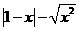 的结果是( )
的结果是( )
A.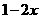 B.
B.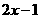 C.
C.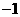 D.
D.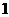
答案:D.
第40题. 实数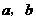 在数轴上对应点
在数轴上对应点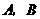 的位置如图,化简
的位置如图,化简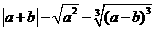 .
.
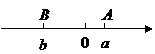
答案:解:由数轴上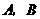 两点的相对位置可知,
两点的相对位置可知,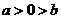 且
且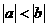 ,
,
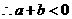 ,
,
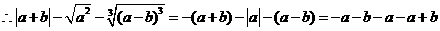
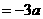 .
.
第41题. 已知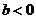 ,则
,则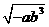 的结果为( )
的结果为( )
A. B.
B.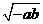 C.
C.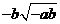 D.
D.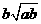
答案:C.
第42题. 若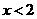 ,化简
,化简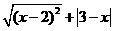 的结果为( )
的结果为( )
A.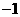 B.
B.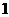 C.
C.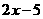 D.
D.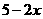
答案:D.
第43题. 下列说法正确的是( )
A.实数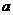 的平方根为
的平方根为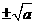 B.
B.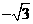 的倒数是
的倒数是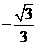
C.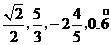 都是分数 D.平方根和其立方根相等的数有
都是分数 D.平方根和其立方根相等的数有
答案:B.
第44题. 若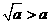 ,且
,且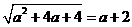 ,则
,则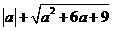 的值为( )
的值为( )
A.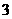 B.
B.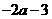 C.
C.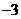 D.
D.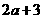
答案:D.
第45题.  的立方根为 ;
的立方根为 ;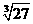 的平方根为 .
的平方根为 .
答案: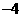 ;
;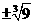 .
.
第46题. 绝对值不大于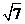 的整数为 .
的整数为 .
答案: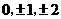 .
.
21.甲、乙两人计算a+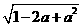 的值,当a=5得到不同的答案.
的值,当a=5得到不同的答案.
甲的解答是:a+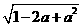 =a+
=a+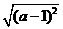 =a+a-1=2a-1=2×5-1=9.
=a+a-1=2a-1=2×5-1=9.
乙的解答是:a+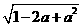 =a+
=a+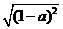 =a+1-a=1
=a+1-a=1
哪一个解答是对的?错误的解答错在哪里?为什么?
20.如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,已知OA=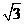 ,AB=1,则点A1的坐标是( )
,AB=1,则点A1的坐标是( )
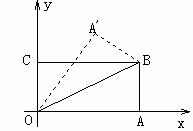
A.(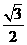 ,
,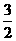 ) B.(
) B.(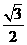 ,3) C.(
,3) C.(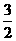 ,
,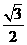 ) D.(
) D.(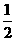 ,
,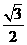 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com