
题目列表(包括答案和解析)
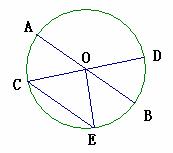
6.如图,已知AB,CD是⊙O的直径,CE是弦,且AB∥CE,∠C=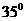 ,则
,则 的度数为
的度数为
答案: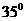
5.(2008襄樊市)如图6,⊙O中OA⊥BC,∠CDA=25°,则∠AOB的度数为 .
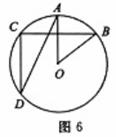
答案.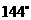
4.如图5,已知 中,
中,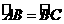 ,且
,且 ,则
,则 ______.
______.

3.(山东滨州)如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠BCE相等的角有( )
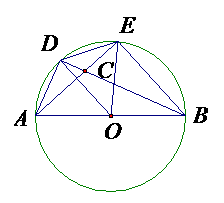
A、2个 B、3个 C、4个 D、5个
答案:C
2. 在 中,
中,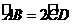 ,那么( )
,那么( )
A. 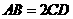
B.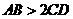
C.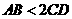
D.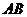 与
与 的大小关系不定。
的大小关系不定。
1.下列三个命题:①圆既是轴对称图形又是中心对称图形;②垂直于弦的直径平分弦;③ 相等的圆心角所对的弧相等.④在同圆或等圆中,如果两条弧相等,那么弦也相等。其中真命题的是( )
A.①② B. ②④ C. ①②④ D. ①②③
答案:A
53. 某农户在承包的荒山上共种植了44棵樱桃树,2002年采摘时,先随意采摘5棵树上的樱桃,称得每棵树上的樱桃重量如下:(单位:千克)
35 35 34 39 37
(1)根据以上数据估计该农户2002年樱桃的产量是多少千克?
(2)已知该农户的这44棵树在2000年共收获樱桃1100千克,若近几年的产量的年增长率相同,依照(1)中估计的2002年产量,预计2003年该农户可收获樱桃多少千克?
52. 已知关于x的方程x2+(2k-3)x+k2=0有两个实数根x1、x2,且x1+x2=x1x2,求k的值。
51.
(02鄂州市)九年义务教育三年制初级中学教科书《代数》第三册第59页的例2是:解方程x4-6x2+5=0。这是一个一元四次方程,根据该方程的特点,它的通常解法是: 设x2=y,那么x4=y2,于是原方程变为 y2-6y+5=0,①,解这个方程,得yl=1,y2=5.当y=l时,x2=1,x=±1; 当y=5时,x2=5,x=±5。 所以原方程有四个根
x1=1,x2=-1,x3= ,x4=-
,x4=- .
.
(1)填空:在由原方程得到方程①的过程中,
利用 法达到降次的目的,体现了 的数学思想;
(2)解方程(x2-x)2-4(x2-x)-12=0.
50.
已知抛物线y= mx2-2mx+4m-
mx2-2mx+4m-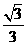 与x轴的两个交点的坐标为A(x1,0),B(x2,0)(xl<x2),且
与x轴的两个交点的坐标为A(x1,0),B(x2,0)(xl<x2),且 =34. (1)求m,x1,x2的值;
(2)在抛物线上是否存在点C,使△ABC是一个顶角为120°的等腰三角形?若存在,请求出所有点C的坐标;若不存在,请说明理由.
=34. (1)求m,x1,x2的值;
(2)在抛物线上是否存在点C,使△ABC是一个顶角为120°的等腰三角形?若存在,请求出所有点C的坐标;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com