3．若一元二次方程x²－2 x－m＝0无实数根，则一次函数y＝(m+1)x+m－1的图象不经过……………………………………………………………………(　　 )

(A)第一象限　 (B)第二象限　 (C)第三象限　 (D)第四象限

[提示]由D ＝4+4 m＜0，得m+1＜0，则m－1＜0，直线过第二、三、四象限．

[答案]A．

[点评]本题综合运用了一元二次方程根的判别式及一次函数图象的性质．注意，题中问的是一次函数图象不经过的象限．

2．二次函数y＝ax²+bx+c 的图象如图，则下列各式中成立的个数是…………(　　 )

(1)abc＜0；　 (2)a+b+c＜0；　 (3)a+c＞b；　 (4)a＜－．

(A)1　　　　　 (B)2　　　　　 (C)3　　　　　 (D)4

[提示]由图象知a＜0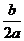，－＞0，故b＞0，而c＞0，则abc＜0．当x＝1时，y＞0，即a+c－b＞0；当x＝－1时，y＜0，即a+c－b＜0．

[答案]B．

[点评]本题要综合运用抛物线性质与解析式系数间的关系．因a＜0，把(4)a＜－两边同除以a，得1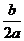＞－，即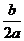－＜1，所以(4)是正确的；也可以根据对称轴在x＝1的左侧，判断出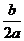－＜1，两边同时乘a，得a＜－，知(4)是正确的．

1．直线y＝3 x－1与y＝x－k 的交点在第四象限，则k 的范围是………………(　　 )

(A)k＜　　 (B)＜k＜1　　 (C)k＞1　　 (D)k＞1或k＜1

[提示]由，解得因点在第四象限，故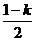＞0，＜0．

∴　 ＜k＜1．

[答案]B．

[点评]本题应用了两函数图象交点坐标的求法，结合了不等式组的解法、象限内点的坐标符号特征等．

21．(8分)已知二次函数y＝ax²+bx+c 的图象抛物线G 经过(－5，0)，(0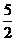，)，(1，6)三点，直线l 的解析式为y＝2 x－3．(1)求抛物线G 的函数解析式；(2)求证抛物线G 与直线l 无公共点；(3)若与l 平行的直线y＝2 x+m 与抛物线G 只有一个公共点P，求P 点的坐标．

《函数》提高测试　　 答案

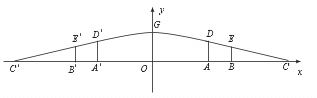
20．(8分)如图是某市一处十字路口立交桥的横断面在平面直角坐标系中的一个示意图，横断面的地平线为x 轴，横断面的对称轴为y 轴，桥拱的D′GD 部分为一段抛物线，顶点G 的高度为8米，AD 和AD′是两侧高为5.5米的立柱，OA 和OA′为两个方向的汽车通行区，宽都为15米，线段CD 和CD′为两段对称的上桥斜坡，其坡度为1∶4．(1)求桥拱DGD′所在抛物线的解析式及CC′的长．(2)BE 和B′E′为支撑斜坡的立柱，其高都为4米，相应的AB 和A′B′为两个方向的行人及非机动车通行区，试求AB 和A′B′的宽．(3)按规定，汽车通过桥下时，载货最高处和桥拱之间的距离不可小于0.4米，今有一大型运货汽车，装载上大型设备后，其宽为4米，车载大型设备的顶部与地面的距离为7米，它能否从OA(OA′)安全通过？请说明理由．

19．(8分)已知正比例函数y＝4 x，反比例函数y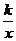＝．(1)当k 为何值时，这两个函数的图象有两个交点？k 为何值时，这两个函数的图象没有交点？(2)这两个函数的图象能否只有一个交点？若有，求出这个交点坐标；若没有，请说明理由．

18．(6分)若函数y＝kx²+2(k+1)x+k－1与x 轴只有一个交点，求k 的值．

17．(6分)已知y＝y₁+y₂，y₁ 与x 成正比例，y₂ 与x 成反比例，并且x＝1时y＝4，x＝2时y＝5，求当x＝4时y 的值．

16．某种火箭的飞机高度h(米)与发射后飞行的时间t(秒)之间的函数关系式是h＝－10 t²+20 t，经过_________秒，火箭发射后又回到地面．

15．公民的月收入超过800元时，超过部分须依法缴纳个人收入调节税，当超过部分不足500元时，税率(即所纳税款占超过部分的百分数)相同．某人本月收入1260元，纳税23元，由此可得所纳税款y(元)与此人月收入x(元)800＜x＜1300间的函数关系为____________．