
题目列表(包括答案和解析)
2、某蔬菜生产基地计划由25个劳动力承包60亩地,种植甲乙丙三种不同的蔬菜,规定每个劳动力只种一种蔬菜,且甲种蔬菜必种,经测算这些不同品种的蔬菜每亩所需的劳动力和预计产值如下表:
|
蔬菜品种 |
甲 |
乙 |
丙 |
|
劳动力/亩(人) |
1/4 |
1/3 |
1/2 |
|
产值/亩(万元) |
0.2 |
0.3 |
0.4 |
应怎样安排才能使每亩地都能种上蔬菜,所有劳动力都有工作,且预计产值达最高,最高产值是多少?
1、 A市和B各有机床12台和6台,现运往C市10台,D市8台,若从A市运一台到C市,D市各需要4万元和8万元,从B市运一台到C市,D市各需3万元和5万元。
(1)设B市运往C市X台,求总费用Y关于X的函数关系式;
(2)若总费用不超过95万元,问共有多少种调运方法?
(3)求总费用最低的调运方法,最低费用是多少万元?
21.(8分)已知二次函数y=ax2+bx+c 的图象抛物线G 经过(-5,0),(0,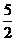 ),(1,6)三点,直线l 的解析式为y=2 x-3.(1)求抛物线G 的函数解析式;(2)求证抛物线G 与直线l 无公共点;(3)若与l 平行的直线y=2 x+m 与抛物线G 只有一个公共点P,求P 点的坐标.
),(1,6)三点,直线l 的解析式为y=2 x-3.(1)求抛物线G 的函数解析式;(2)求证抛物线G 与直线l 无公共点;(3)若与l 平行的直线y=2 x+m 与抛物线G 只有一个公共点P,求P 点的坐标.
[分析](1)略;(2)要证抛物线G 与直线l 无公共点,就是要证G 与l 的解析式组成的方程无实数解;(3)直线y=2 x+m 与抛物线G 只有一个公共点,就是由它们的解析式组成的二元二次方程组有一个解,求出这组解,就得P 点的坐标.
[解](1)∵ 抛物线G 通过(-5,0),(0,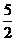 ),(1,6)三点,
),(1,6)三点,
∴
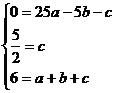 ,
,
解得
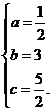
∴ 抛物线G的解析式为y= x2+3 x+
x2+3 x+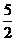 .
.
(2)由 ,
,
消去y,得 x2+x+
x2+x+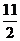 =0,
=0,
∵ D=12-4× ×
×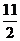 =-10<0,
=-10<0,
∴ 方程无实根,即抛物线G 与直线l 无公共点.
(3)由 ,消去y,得
,消去y,得
 x2+x+
x2+x+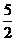 -m=0.
①
-m=0.
①
∵ 抛物线G 与直线y=2 x+m 只有一个公共点P,
∴ D =12-4× ×(
×(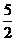 -m)=0.
-m)=0.
解得m=2.
把m=2代入方程①,解得x=-1.
把x=-1代入y= x2+3 x+
x2+3 x+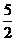 ,得y=0.
,得y=0.
∴ P(-1,0).
[点评]本题综合运用了二次函数解析式的求法.抛物线与直线的交点等知识,其关键是把函数问题灵活转化为方程知识求解.
20.(8分)如图是某市一处十字路口立交桥的横断面在平面直角坐标系中的一个示意图,横断面的地平线为x 轴,横断面的对称轴为y 轴,桥拱的D′GD 部分为一段抛物线,顶点G 的高度为8米,AD 和AD′是两侧高为5.5米的立柱,OA 和OA′为两个方向的汽车通行区,宽都为15米,线段CD 和CD′为两段对称的上桥斜坡,其坡度为1∶4.(1)求桥拱DGD′所在抛物线的解析式及CC′的长.(2)BE 和B′E′为支撑斜坡的立柱,其高都为4米,相应的AB 和A′B′为两个方向的行人及非机动车通行区,试求AB 和A′B′的宽.(3)按规定,汽车通过桥下时,载货最高处和桥拱之间的距离不可小于0.4米,今有一大型运货汽车,装载上大型设备后,其宽为4米,车载大型设备的顶部与地面的距离为7米,它能否从OA(OA′)安全通过?请说明理由.
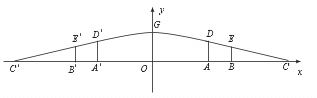
[分析]欲求函数的解析式,关键是求出三个独立的点的坐标,然后由待定系数法求之.所以关键是由题中线段的长度计算出D、G、D′的坐标,当然也可由对称轴x=0解之.
至于求CC′、AB、A′B′的数值,则关键是由坡度的定义求解之;到底能否安全通过,则只需在抛物线的解析式中令x=4,求出相应的y 值,即可作出明确的判断.
[解](1)由题意和抛物线的对称轴是x=0,可设抛物线的解析式为y=ax2+c.
由题意得G(0,8),D(15,5.5)
∴ 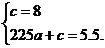
∴ 
∴ y=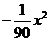 +8.
+8.
又 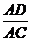 =
=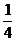 且AD=5.5,
且AD=5.5,
∴ AC=5.5×4=22(米).
∴ CC′=2C=2×(OA+AC)=2×(15+22)=74(米).
∴ CC′的长是74米.
(2)∵  =
=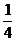 ,BE=4,
,BE=4,
∴ BC=16.
∴ AB=AC-BC=22-16=6(米).
A′B′=AB=6(米).
(3)此大型货车可以从OA(OA′)区域安全通过.
在y=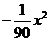 +8中,当x=4时,y=-
+8中,当x=4时,y=-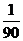 ×16+8=
×16+8=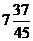 ,而
,而
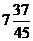 -(7+0.4)=
-(7+0.4)=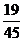 >0,
>0,
∴ 可以从OA 区域安全通过.
19.(8分)已知正比例函数y=4 x,反比例函数y=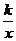 .(1)当k 为何值时,这两个函数的图象有两个交点?k 为何值时,这两个函数的图象没有交点?(2)这两个函数的图象能否只有一个交点?若有,求出这个交点坐标;若没有,请说明理由.
.(1)当k 为何值时,这两个函数的图象有两个交点?k 为何值时,这两个函数的图象没有交点?(2)这两个函数的图象能否只有一个交点?若有,求出这个交点坐标;若没有,请说明理由.
[解]由y=4 x
和y=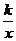 ,得
,得
4 x2-k=0,D =16 k.
(1)当D >0,即k>0时,两函数图象有两个交点;
当D <0,即k<0时,两函数图象没有交点;
(2)∵ 比例系数k≠0,故D ≠0.
∴ 两函数图象不可能只有一个交点.
18.(6分)若函数y=kx2+2(k+1)x+k-1与x 轴只有一个交点,求k 的值.
[提示]本题要分k=0,k≠0两种情况讨论.
[解]当k=0时,y=2 x-1,是一次函数,此时,直线与x 轴必有一个交点.
当k≠0时,函数为二次函数,
此时,D =4(k+1)2-4 k(k-1)
=12 k+4=0.
∴ k=- .
.
∴ 所求的k 值为0或- .
.
[点评]注意,当问题中未指明函数形式,而最高次项系数含字母时,要注意这个系数是否为0.函数图象与x 轴有一个交点包括两种情形:当函数是一次函数时,直线与x 轴必只有一个交点;当函数是二次函数时,在D =0的条件下,图象与x 轴只有一个交点.
17.(6分)已知y=y1+y2,y1 与x 成正比例,y2 与x 成反比例,并且x=1时y=4,x=2时y=5,求当x=4时y 的值.
[解]设y1=k1x,y2=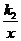 ,则y=k1x+
,则y=k1x+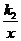 .
.
把x=1时y=4,x=2时y=5分别代入上式,得
 ,
,
解得
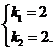
∴ 函数解析式为y=2 x+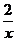 .
.
当x=4时,y=2×4+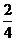 =
= .
.
∴ 所求的y 值为 .
.
[点评]本题考查用待定系数法求函数解析式.关键在于正确设出y1,y2 与x 的函数解析式.注意两个比例系数应分别用k1,k2 表示出来,而不能仅用一个k 值表示.
16.某种火箭的飞机高度h(米)与发射后飞行的时间t(秒)之间的函数关系式是h=-10 t2+20 t,经过_________秒,火箭发射后又回到地面.
[提示]火箭返回地面,即指飞行高度为0,则-10 t2+20 t=0,故t=0或t=20.
[答案]20.
[点评]注意:t=0应舍去的原因是此时火箭虽在地面,但未发射,而不是返回地面.
15.公民的月收入超过800元时,超过部分须依法缴纳个人收入调节税,当超过部分不足500元时,税率(即所纳税款占超过部分的百分数)相同.某人本月收入1260元,纳税23元,由此可得所纳税款y(元)与此人月收入x(元) 800<x<1300
800<x<1300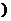 间的函数关系为____________.
间的函数关系为____________.
[提示]因1260-800=460, =5%,故在800<x<1300时的税率为5%.
=5%,故在800<x<1300时的税率为5%.
[答案]y=5%(x-800).
[点评]本题是与实际问题相关的函数关系式,解题时应注意并不是每个人月收入的全部都必须纳税,而是超过800元的部分才纳税,故列函数式时月收入x须减去800.
14.若一次函数y=kx+b 的自变量x 的取值范围是-2≤x≤6,相应函数值y 的范围是-11≤y≤9,则函数解析式是___________.
[提示]当k>0时,有 ,解得
,解得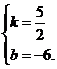
当k<0时,有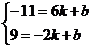 ,解得
,解得
[答案]y=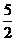 x-6或y=-
x-6或y=-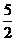 x+4.
x+4.
[点评]因k 是待定字母,而k 的不同取值,导致线段分布象限不一样,自变量的取值与函数取值的对应关系也就不同.故本例要分k>0时自变量最大值对应函数最大值,与k<0时自变量最大值对应函数最小值两种情形讨论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com