47.　　 　以x为自变量的二次函数y＝－x²+2x+m，它的图象与y轴交于点C(0,3)，与x轴交于点A、B，点A在点B的左边，点O为坐标原点．(1)求这个二次函数的解析式及点A，点B的坐标，画出二次函数的图象； (2)在x轴上是否存在点Q，在位于x轴上方部分的抛物线上是否存在点P，使得以A，P,Q三点为顶点的三角形与ΔAOC相似(不包含全等)?若存在，请求出点P，点Q的坐标；

姓名　　　 班级　　 学号　　　

46.　　 已知二次函数(1)证明：不论a取何值，抛物线的顶点Q总在x轴的下方；(2)设抛物线与y轴交于点C，如果过点C且平行于x轴的直线与该抛物线有两个不同的交点，并设另一个交点为点D，问：△QCD能否是等边三角形？若能，请求出相应的二次函数解析式；若不能，请说明理由；(3)在第(2)题的已知条件下，又设抛物线与x轴的交点之一为点A，则能使△ACD的面积等于的抛物线有几条？请证明你的结论.

45.　　 分)已知：如图，一次函数的图象经过第一、二、三象限，且与反比例函数的图象交于A、B两点，与Y轴交于点C，与X轴交于点D，OB=，tg∠DOB=1/3。(1)求此反比例函数的解析式；(2)设点A的横坐标为m，ΔABO的面积为S，求S与m的函数关系式，并写出自变量m的取值范围；(3)当ΔOCD的面积等于S/2时，试判断过A、B两点的抛物线在X轴上截得的线段长能否等于3，如果能，求出此时抛物线的解析式；如果不能，请说明理由。

44.　　 某企业有员工300人，生产∠种产品，平均每人每年可创造利润m万元(m 为大于零的常数)。为减员增效，决定从中调配x人去生产新开发的B种产品，根据评估，调配后，继续生产A种产品的员工平均每人每年创造的利润可增加20%，生产B种产品的员工平均每人每年可创造利润1.54m万元。

(1)　　　 调配后，企业生产∠种产品的年利润为____________万元，企业生产B种产品的年利润为_________________万元(用含x和m的代数式表示)。若设调配后企业全年总利润为y万元，则y关于x的函数解析式为____________.

(2)　　　 若要求调配后，企业生产A种产品的年利润不小于调配前企业年利润的，生产B种产品的年利润大于调配前企业年利润的一半，应有哪几种调配方案 ？请设计出来，并指出其中哪种方案全年总利润最大(必要时，运算过程可保留3个有效数字)。

(3)　　　 企业决定将(2)中的年最大总利润(设m＝2)继续投资开发新产品。现有6种产品可供选择(不得重复投资同一种产品)各产品所需资金及所获年利润如下表：

如果你是企业决策者，为使此项投资所获年利润不少于145万元，你可以投资开发哪些产品？请写出两种投资方案。

43.　　 已知一次函数的图象分别交x轴、y轴于A、B两点，且与反比例函数的图象在第一象限交于点C(4，n)，CD⊥x轴于D。(1)求m、n的值，并在给定的直角坐标系中作出一次函数的图象； (2)如果点P、Q分别从A、C两点同时出发，以相同的速度沿线段AD、CA向D、A运动，设AP＝k。①k为何值时，以A、P、Q为顶点的三角形与△AOB相似？②k为何值时，△APQ的面积取得最大值？并求出这个最大值。

42.　　 如图已知一交函数y=-2x+6的图象与x轴交于点A，与y轴交于点C；二次函数y=ax²+bx+c(a≠0)的图象过A、C两点，并且与x轴交于另一点B(B在负半轴上)。(1)当S_△ABC=4S_△B0C时，求抛物线y=ax²+bx+c的解析式和此函数顶点坐标。(2)以OA的长为直径作⊙M，试判定⊙M与直线AC的位置关系，并说明理由。

41.　　 如图，已知平面直角坐标系中三点A(4，0)，(0，4)，P(x，0)(x＜0)，作PC⊥PB交过点A的直线l于点C(4，y)。(1)求y关于x的函数解析式；(2)当x取最大整数时，求BC与PA的交点Q坐标；

40.　　 已知：抛物线y＝ax²+bx+c与y轴交于点C，与x轴交于点A(x₁，0)，b(x₂，0)(x₁<x₂)，顶点M的纵坐标是－4。若x₁，x₂是方程x²―2(m―1)+m²－7＝0的两个实数根，且。(1)求A、B两点的坐标；(2)求抛物线的解析式；(3)在抛物线上是否存在点P，使△PAB的面积等于四边形ACMB的面积的2倍？若存在，求出所有合条件的点P的坐标；若不存在，请说明理由。

39.　　 已知抛物线过点A(－2，0)、B(1，0)、C(0，2)三点。(1)求此抛物线的解析式；(2)在这条抛物线上是否存在点P，使∠AOP=45⁰？若存在，请求出点P的坐标；若不存在，请说明理由。

38.　　 中华人民共和国个人所得税》规定，公民月工资、薪金所得不超过800元的部分不必纳税，超过800元的部分为全月应纳税年得额。此项税款按下表累进计算：

(纳税款=应纳税额所得额对应的税率)

按此规定解下列问题：(1)设某甲的月工资、薪金所得为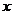元(1300<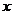<2800)，需缴交的所得税款为元，试写出与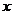的函数关系式；(2)若某乙一月份应缴交所得税款95元，那么他一月份的工资、薪金是多少元？