
题目列表(包括答案和解析)
7.等腰三角形一边等于5,另一边等于8,则周长是 ;
6.如果三角形有两边的长分别为5a,3a,则第三边x必须满足的条件是 ;
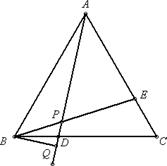
已知:如图,在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连 结AD、BE交于点P,作BQ⊥AD,垂足为Q.求证:BP=2PQ.
《三角形》基础测试 答案
一 填空题(每小题3分,共18分):
5.在△ABC中,∠A -∠C = 25°,∠B -∠A = 10°,则∠B = ;
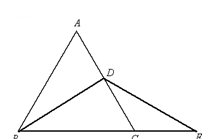
已知:如图,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使 CE = CD.求证:BD = DE.
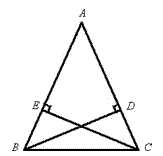
于E,BD⊥AC于D,求证:BD=CE.
已知D是Rt△ABC斜边AC的中点,DE⊥AC交BC于E,且∠EAB∶∠BAC=2∶5,求∠ACB的度数.
已知:如图,AD是△ABD和△ACD的公共边.
求证:∠BDC =∠BAC +∠B +∠C.
2.可能性相等.
第24题. 下面是分别装有黑白棋子数不同的5个罐子(如下图)

(1)列出从各罐中随意摸出一枚棋子,摸到白子的可能性大小关系;
(2)若从罐中随意摸出一枚黑子是必然事件,是从哪个罐中摸出的棋子;
(3)若从罐中随意摸出一枚棋子,摸到白子的可能性比摸到黑子的可能性大,是从哪个罐中摸出的棋子;
(4)若从罐中随意摸出一枚棋子,摸到白子与摸到黑子的可能性相等,是从哪个罐中摸出的棋子.
答案:(1)E>D>C>B>A;(2)从A罐中;(3)从D或E罐中;(4)从C罐中.
第25题. 下图分别是代号为A,B,C的三个转盘,各转盘上的4个区域除颜色外都相同.试问:

(1)停止后指针对准红色区域比对准黄色区域的可能性大,应旋转哪个转盘,为什么?
(2)停止后指针对准红色与黄色区域的可能性相等,应旋转哪个转盘?为什么?
(3)停止后指针对准黄色比对准红色区域的可能性大,应旋转哪个转盘?为什么?
(4)若同时旋转A,B转盘,停止后两枚指针同时对准哪一种颜色区域的可能性大?为什么?
(5)若同时旋转A,B转盘,列出停止后两枚指针同时对准红色区域,同时对准黄色区域和分别对准两种颜色区域,这三种可能性的大小关系,(从大到小列出).
答案:(1)旋转转盘B,只有B中红色区域比黄色区域数量多;
(2)旋转转盘A,只有A中红色与黄色区域数量相等;
(3)旋转转盘C,只有C中黄色区域比红色区域数量多;
(4)同时旋转转盘A,B两枚指针同时对准两种颜色区域的所有机会如下表:
 |
红 |
红 |
红 |
黄, |
|
红 |
(红红) |
(红红) |
(红红) |
(红黄) |
|
黄 |
(黄红) |
(黄红) |
(黄红) |
(黄黄) |
|
红 |
(红红) |
(红红) |
(红红) |
(红黄) |
|
黄 |
(黄红) |
(黄红) |
(黄红) |
(黄黄) |
两枚指针同时对准“红色”的机会有6个,同时对准“黄色”的机会有2个,所以,同时对准“红色”区域的可能性最大(因为机会最多);
(5)一枚指针对准红色,另一枚对准黄色的机会有8个.所以,三种可能性的大小关系是:分别对准两种颜色>同时对准红色>同时对准黄色.
第26题. 某商场为了吸引顾客,设立了一个可以自由转动的转盘,转盘上有21个形状相同面积相等的区域,其中7个有奖区域均匀分布在转盘上.有奖区域中标明奖励购物券的金额,奖励100元的区域1个,50元的区域2个,20元的区域4个.规定:顾客每购买100元的商品,就能获得转动一次转盘的机会,转盘停止后,指针对准有奖区域,顾客就可以获得这个区域上标明金额的购物券.
某顾客购买了140元的商品,可以转动一次转盘.
(1)他获得与没有获得购物券的可能性哪个大?
(2)如果获得购物券,获得哪种金额购物券的可能性最大?哪种可能性最小?
答案:(1)没有获得购物券的可能性大;(2)得20元的可能性最大,得100元的可能性最小.
第27题. 一个盒子里,装有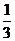 的黄球,还有红球和白球,除此以外没其他颜色的球,只知道红球和白球的数量相差很大,不能倒出来一个个数,你能有办法估计哪种颜色的球可能最多?说说你的方法和理由.
的黄球,还有红球和白球,除此以外没其他颜色的球,只知道红球和白球的数量相差很大,不能倒出来一个个数,你能有办法估计哪种颜色的球可能最多?说说你的方法和理由.
答案:随意从盒子摸出若干球,数出其中红球、黄球和白球的数量后放回盒子里,搅匀后再摸出若干个球,再数出其中各种颜色球的数量……试验若干次,每次或比较多的次数哪种颜色的球最多,盒子里这种颜色的球最多.
第28题. 把转盘面划分作8等分扇形,其中3个扇形涂成红色,另5个扇形涂成白色,那么转盘停止转动后,指针指着红色和指针指着白色扇形上的可能性比较( )
A.红色比白色的可能性大 B.红色和白色的可能性相等
C.红色是白色的可能性的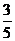 D.红色是白色的可能性的
D.红色是白色的可能性的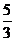
答案:C.
第29题. 布袋内装有表面光滑、大小相同、同一种材料制成的10个红色小球,从袋中任意摸取一个小球是红色球的事件是_________事件,此事件出现的可能性大小是__________,从袋中任意摸取一个小球是白色球的事件是_______事件,此事件出现的可能性的大小是___________.
答案:必然,1,不可能,0.
第30题. 两次投掷一枚硬币.①两次都是正面朝上的事件发生的可能性,②一正一反朝上的事件发生的可能性,③至少有一次正面朝上的事件发生的可能性,它们的大小关系是___________(用①②③代码表示可能性).
答案:①<②<③.
第31题. 北京地铁二线内环列车,平均每隔4分钟就有一列列车经过某地铁站,一列列车从该站开出环行40分钟回到该站,已知该线上有6列新的列车,其余为原来的列车,张华从该车站乘内环列车.
(1)张华乘坐的哪种列车的可能性最大?哪种列车的可能性最小;
(2)最小可能性是最大可能性的几分之几.
答案:(1)乘坐新的列车可能性大,原来的列车可能性小;(2)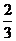 .
.
第32题. 袋子里有1个红球,3个白球和5个黄球,每个球除颜色外均相同,从中任意摸出1个球,则摸到红球的可能性_____,摸到黄球的可能性_____(填“大”与“小”).
答案:小,大.
第33题. 右图是一个可以自由转动的转盘,转动这个转盘,指针最可能指向的颜色是( )
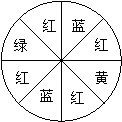 A.红色 B.黄色 C.绿色 D.蓝色
A.红色 B.黄色 C.绿色 D.蓝色
答案:A.
第34题. 有一块手表不知何时停表,秒针停在下列范围:①12点至4点(含12点,不含4点,下同),②4点至5点,③5点至10点,④10点至12点.出现的可能性分别依次用 表示,则它们的大小关系是( )
表示,则它们的大小关系是( )
A.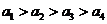 B.
B.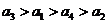
C.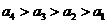 D.
D.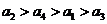
答案:B.
第35题. 从除去大、小王以外的52张扑克牌中随意取出一张,取到方块的可能性是 ,红色牌的可能性是
,红色牌的可能性是 ,牌上有字母的可能性是
,牌上有字母的可能性是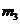 ,牌上有数字的可能性是
,牌上有数字的可能性是 .则它们当中最大和最小的是( )
.则它们当中最大和最小的是( )
A. 最大,
最大, 最小 B.
最小 B. 最大,
最大,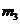 最小
最小
C. 最大,
最大, 最小 D.
最小 D.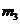 最大,
最大, 最小
最小
答案:A.
第36题. 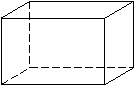 如下图所示,一个正六面体,每个面只有一种颜色,六个面只有红、绿两种颜色.任意掷一枚这样的正六面体,若面朝上是红色的可能性大于是绿色的可能性,则绿色面的数量可能是____________.
如下图所示,一个正六面体,每个面只有一种颜色,六个面只有红、绿两种颜色.任意掷一枚这样的正六面体,若面朝上是红色的可能性大于是绿色的可能性,则绿色面的数量可能是____________.
答案:1或2.
第37题. 任意掷一枚骰子,下列面朝上的点数:
①点数小于1;②点数等于1;③点数大于1;④点数大于0;⑤点数小于7;⑥点数等于6.
(1)哪些必然出现?哪些不可能出现?哪些不一定出现也不一定不出现?
(2)将上面6种面朝上点数出现的可能性的大小关系排列出来.
答案:(1)“点数大于0”与“点数小于7”必然出现;“点数小于1”不可能出现;“点数等于1”、“点数大于1”和“点数等于6”不一定出现也不一定出现;
(2)它们出现的可能性大小关系是:“点数小于1”<“点数等于1”=“点数等于6”<“点数大于1”<“点数大于0”=“点数小于7”.
第38题. 一个罐子里只有5个红球3个白球,它们的大小和质量相同,从罐子里随意同时摸出7个球,试问:摸到的这7个球中,5个红球2个白球的可能性和4个红球3个白球的可能性,哪个大?
答案:因为红球比白球多,所以留下1个红球比留下1个白球的可能性大.
所以,留下的1个红球比1个白球的可能性大,即取出4个红球3个白球比取出5个红球2个白球的可能性大.
第39题. 张大伯家有3个小孩,甲猜3个都是男孩,乙猜3个都是女孩,丙猜2个男孩1个女孩,丁猜2个女孩1个男孩.试问谁猜对的可能最大.
答案:丙和丁猜对的可能性都最大.
第40题. 任意掷一枚骰子点数小于3的面朝上的可能性,张师傅一周内有2天倒班(不一定是星期六和星期日)休假,随意一天去找张师傅他正好在休假的可能性.试问哪个可能性大?
答案:点数小于3的面朝上的可能性大.
2.摸到数字为偶数和数字为奇数的可能性怎样?
答案:1.摸到3和5的可能性相等,摸到3和4的可能性比4相同工异曲.
1.摸到3和5的可能性哪个大?摸到3和4的可能性哪个大?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com