2、在Rt△ABC中，∠C＝90°，a＝4，c＝5，则 sinA＝＿＿＿＿。

1、△ABC中，AB＝AC，∠B＝50°，则∠A＝＿＿＿＿。

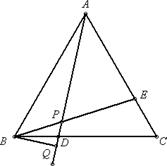
已知：如图，在等边三角形ABC中，D、E分别为BC、AC上的点，且AE＝CD，连　结AD、BE交于点P，作BQ⊥AD，垂足为Q．求证：BP＝2PQ.

提示：

只需证　∠PBQ＝30°.

由于　△BAE≌△ACD，

所以　∠CAD ＝∠ABE，

则有　∠BPQ ＝∠PBA+∠BAP ＝∠PAE +∠BAD ＝ 60°，

可得　∠PBQ＝30°.

已知：如图，在等边三角形ABC的AC边上取中点D，BC的延长线上取一点E，使 CE ＝ CD．求证：BD ＝ DE．

提示：可知∠DBC＝30°，只需证出∠DEB ＝ 30°．由∠ACE ＝ 120°，得∠CDE+∠E＝60°，

所以∠CDE ＝∠E＝30°，则有BD ＝ DE．

已知：如图，AB＝AC，CE⊥AB于E，BD⊥AC于D，求证：BD＝CE.

提示：

由AB ＝ AC得∠B ＝∠C，

又有 　BC ＝ BC，

可证　△ABD≌△ACE，

从而有　BD ＝ CE.

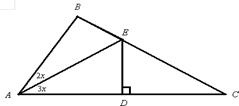
已知D是Rt△ABC斜边AC的中点，DE⊥AC交BC于E，且∠EAB∶∠BAC＝2∶5，求∠ACB的度数.

提示：利用列方程的方法求解．

设∠EAB＝2x°，∠BAC＝5x°，

　则　∠ACB＝3x°，

于是得方程

5x°+3x°＝90°，

解得　　 x°＝，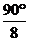

∴ ∠ACB＝33.75°.　　　　　　　　　　　　　　　　　 　

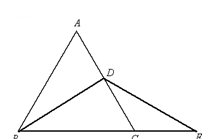
已知：如图，AD是△ABD和△ACD的公共边.

求证：∠BDC ＝∠BAC +∠B +∠C.提示：延长AD到E，把∠BDC归结为△ABD和△ACD的外角，

利用“三角形外角等于不相临的两个内角的和”可以证明.

4．已知：如图，在△ABC中，AB＝AC，BC＝BD，AD＝DE＝EB，则∠A的度数是…………………………………………………………………………(　　 )

(A)30°　　 (B)36°　　　 (C)45°　　　 (D)54°

答案：1．B；　2．C；　3．C；　4．C．

3．一个等腰三角形底边的长为5cm，一腰上的中线把其周长分成的两部分的差为3 cm，则腰长为 ………………………………………………………(　　 )

(A)2 cm　　 　 (B) 8 cm　　　　 (C)2 cm 或8 cm　 　 (D)10 cm

2.下列两个三角形中，一定全等的是…………………………………………(　　 )

(A)有一个角是40°，腰相等的两个等腰三角形(B)两个等边三角形

(C)有一个角是100°，底相等的两个等腰三角形

(D)有一条边相等，有一个内角相等的两个等腰三角形