
题目列表(包括答案和解析)
一艘船向正东方先航行,上午10点在灯塔的西南方向k海里处,到下午2点时航行到灯塔的东偏南60°的方向,画出船的航行方位图,并求出船的航行速度.
解:如图,依题意,灯塔位于P点,船丛A 点向东航行,12点到达C点,
且有 PB⊥AC,A=45°,∠BPC=30°;
 于是,在△ABP中,有
于是,在△ABP中,有
AB=PB=AP cos45° =k 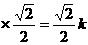 .
.
在△PBC中,又有BC=PB tan30°=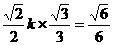 k,
k,
所以AC= .
.
可知船的航行速度为
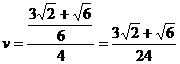 .
.
略解:利用角平分线的性质,构造直角三角形:作CE⊥AB于E,CF⊥AD于F,易证CEB≌△CFD,则有EB=FD;又可证△CEA≌△CFA,于是由 AE=AF 可得21-EB=9+FD,∴ EB=FD=6;
在Rt△AFC中,有AC=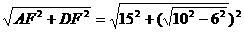
=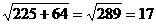 .
.
4.已知:B=30°,CD为AB边上的高,且CD=4.
解:如图,CD=4,在Rt△CDB 中,有BC=a=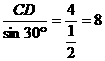 ,A=60°;
,A=60°;
另一方面,有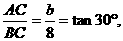 ∴
∴ 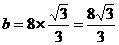
c=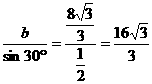 .
.
3.已知:c边上的高h=4,b=5;
解:依题意,有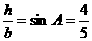 ∴∠A≈53°8′,B≈36°52′;
∴∠A≈53°8′,B≈36°52′;
另一方面,有a=b tan A=5× =5×
=5×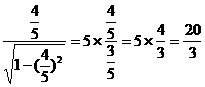
∴ sinA=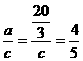 , ∴c=
, ∴c=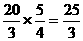
2.已知:∠B=45°,a+b=10;
解:依题意,∠A=∠B=45°, 所以a=b=5;
由 sinA=sin45°=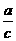 得 ∴
得 ∴  , ∴c=
, ∴c=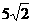 .
.
1.已知:b= ,
, ;
;
解:S△ABC= , ∴ a=10.
, ∴ a=10.
∴ tanA=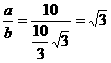 . ∴ ∠A=60°,∠B=30°,
. ∴ ∠A=60°,∠B=30°,
∴ c=2b=2
 =
= .
.
 一艘船向正东方先航行,上午10点在灯塔的西南方向k海里处,到下午2点时航行到灯塔的东偏南60°的方向,画出船的航行方位图,并求出船的航行速度.
一艘船向正东方先航行,上午10点在灯塔的西南方向k海里处,到下午2点时航行到灯塔的东偏南60°的方向,画出船的航行方位图,并求出船的航行速度.
解:
《解直角三角形》提高测试 答案
一 选择题答案:1.C;2.D;3.A;4.C;5.D.
二 填空题答案:1. ; 2.sin90°,cos0°,tan45°,cot45°;
; 2.sin90°,cos0°,tan45°,cot45°;
3.tan50°-tan40°; 4.0; 5.a(a+b)2.
三 解下列直角三角形:在直角三角形ABC中,∠C=90°:△
在四边形ABCD中,AC恰好平分∠A,AB=21,AD=9,BC=CD=10,试求AC的长.
解:
60.如图,等腰梯形ABCD中,AD∥BC,tgB=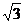 ,上底AD=10,梯形的高是6,求(1)∠B的度数;(2)下底BC的值。(结果保留根号)
,上底AD=10,梯形的高是6,求(1)∠B的度数;(2)下底BC的值。(结果保留根号)

59. 如图,点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C,求证:AD=AE。
如图,点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C,求证:AD=AE。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com