
题目列表(包括答案和解析)
22、解:(1)500;
(2)如图1;
(3)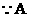 型号发芽率为
型号发芽率为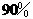 ,B型号发芽率为
,B型号发芽率为 ,
,
D型号发芽率为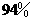 ,C型号发芽率为
,C型号发芽率为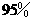 .
.
 应选C型号的种子进行推广.
应选C型号的种子进行推广.
(4)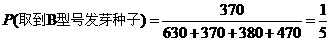 .
.
21、解:(1)图形平移的距离就是线段BC的长
又∵在Rt△ABC中,斜边长为10cm,∠BAC=30,∴BC=5cm,
∴平移的距离为5cm.
(2)∵∠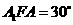 ,∴∠
,∴∠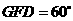 ,∠D=30°.
,∠D=30°.
∴∠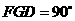 .
.
在RtEFD中,ED=10 cm,∵FD=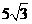 ,
,
∵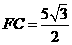 cm.
cm.
(3)△AHE与△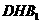 中,∵
中,∵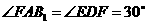 ,
,
∵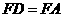 ,
,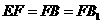 ,
,
∴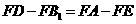 ,即
,即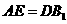 .
.
又∵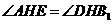 ,∴△
,∴△ ≌△
≌△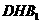 (AAS).
(AAS).
∴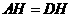 .
.
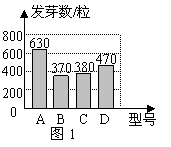
20、解:(1)特征1:都是轴对称图形;特征2:都是中心对称图形;特征3:这些图形的面积都等于4个单位面积;等
(2)满足条件的图形有很多,只要画正确一个,都可以得满分.

19、解:(1)依题意,得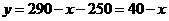
(2)依题意,得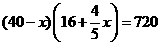
解得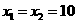
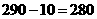
答:每吨水泥的实际售价应定为 元时,每天的销售利润平均可达720元.
元时,每天的销售利润平均可达720元.
注:第(1)题中函数关系式写为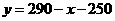 者不扣分.
者不扣分.
18、略
17、(1)证明:
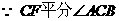 ,
,
∴ 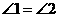 .
.
又∵ 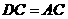 ,
,
∴ CF是△ACD的中线,
∴ 点F是AD的中点.
∵ 点E是AB的中点,
∴ EF∥BD,
即 EF∥BC.
(2)解:由(1)知,EF∥BD,
∴ △AEF∽△ABD ,
∴ 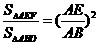 .
.
又∵ 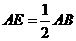 ,
,
 ,
,
∴ 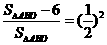 ,
,
∴ 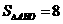 ,
,
∴ 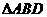 的面积为8.
的面积为8.
9、76 10、1 11、27 12、7或8 13、6.4 14、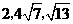 15、3 16、2
15、3 16、2
BAABCBDC
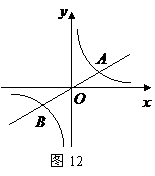
25.(本题满分12分)如图12,已知直线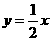 与双曲线
与双曲线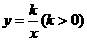 交于
交于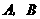 两点,且点
两点,且点 的横坐标为
的横坐标为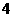 .(1)求
.(1)求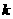 的值;
的值;
(2)若双曲线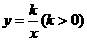 上一点
上一点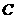 的纵坐标为8,求
的纵坐标为8,求 的面积;
的面积;
 (3)过原点
(3)过原点 的另一条直线
的另一条直线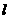 交双曲线
交双曲线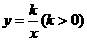 于
于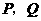 两点(
两点( 点在第一象限),若由点
点在第一象限),若由点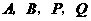 为顶点组成的四边形面积为
为顶点组成的四边形面积为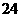 ,求点
,求点 的坐标.
的坐标.
23.(本题满分8分)张彬和王华两位同学为得到一张观看足球比赛的入场券,各自设计了一种方案:
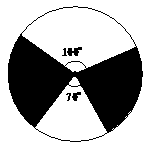
张彬:如图,设计了一个可以自由转动的转盘,随意转动转盘,当指针指向阴影区域时,张彬得到了入场券;否则,王华得到入场券;
王华:将三个完全相同的小球分别标上数字1、2、3后,放入一个不透明的袋子中.从中随机取出一个小球,然后放回袋子;混合均匀后,再随机取出一个小球.若两次取出的小球上的数字之和为偶数,王华得到入场券;否则,张彬得到入场券.
请你运用所学的概率知识,分析张彬和王华 的设计方案对双方是否公平.
24.(本小题满分8分)如图①,在等腰梯形ABCD中,AB∥CD,E、F是边AB上的两点,且AE=BF,DE与CF相交于梯形ABCD内一点O.
(1)求证:OE=OF;
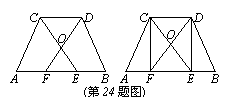 (2)如图②,当EF=CD时,请你连接DF、CE,判断四边形DCEF是什么样的四边形,并证明你的结论.
(2)如图②,当EF=CD时,请你连接DF、CE,判断四边形DCEF是什么样的四边形,并证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com