
题目列表(包括答案和解析)
8.如图是10把相同的折扇组成的“蝶恋花”(图①)和梅花图案(图②)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为 度。
7.在直角坐标系中有两点A(4,0),B(0,2),如果点C在 轴上(C与B不重合),当点C的坐标为
轴上(C与B不重合),当点C的坐标为
时,使得由点B、O、C显顶点组成的三角形与△AOB相似。(至少找出两种满足条件的点的坐标)
6.一个圆锥的底面半径为3㎝,侧面展开图为半圆,则该圆锥的高是 ㎝;
5.黄冈中学是百年名校,百年校庆上的焰火晚会令很多人记忆犹新。有一种焰火升高高度为 与飞行时间
与飞行时间 的关系式是
的关系式是 ,若这种焰火在点燃升空后到最高处引爆,则从点火到引爆所需时间为
;
,若这种焰火在点燃升空后到最高处引爆,则从点火到引爆所需时间为
;
4.如图AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,则∠D= ;
3. 已知二次函数
已知二次函数 部分图象如图所示,则关于
部分图象如图所示,则关于 的一元二次方程
的一元二次方程 的解为
;
的解为
;


2.生物学家发现一种病菌的长度为 ,用科学方法表示
,用科学方法表示 的结果为 ;
的结果为 ;
1.  ;
; 的相反数为 ;
的相反数为 ; ;
;
25、解:(1)∵点A横坐标为4 , ∴当 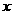 = 4时,
= 4时,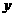 = 2 .
= 2 .
∴ 点A的坐标为( 4,2 ).
∵ 点A是直线 与双曲线
与双曲线 (k>0)的交点 ,
(k>0)的交点 ,
∴ k = 4 ×2 = 8 .
(2) 解法一:如图12-1,
∵ 点C在双曲线 上,当
上,当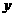 = 8时,
= 8时,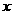 = 1
= 1
∴ 点C的坐标为 ( 1, 8 ) .
过点A、C分别做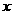 轴、
轴、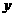 轴的垂线,垂足为M、N,得矩形DMON .
轴的垂线,垂足为M、N,得矩形DMON .
S矩形ONDM= 32 , S△ONC = 4 , S△CDA = 9, S△OAM = 4 .
S△AOC= S矩形ONDM - S△ONC - S△CDA - S△OAM = 32 - 4 - 9 - 4 = 15 .
 解法二:如图12-2,
解法二:如图12-2,
过点 C、A分别做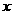 轴的垂线,垂足为E、F,
轴的垂线,垂足为E、F,
∵ 点C在双曲线 上,当
上,当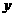 = 8时,
= 8时,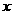 = 1 .
= 1 .
∴ 点C的坐标为 ( 1, 8 ).
∵ 点C、A都在双曲线 上 ,
上 ,
∴ S△COE = S△AOF = 4 。
∴ S△COE + S梯形CEFA = S△COA + S△AOF .
∴ S△COA = S梯形CEFA .
 ∵ S梯形CEFA =
∵ S梯形CEFA =  ×(2+8)×3 = 15 ,
×(2+8)×3 = 15 ,
∴ S△COA = 15 .
(3)∵ 反比例函数图象是关于原点O的中心对称图形 ,
∴ OP=OQ,OA=OB .
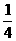 ∴ 四边形APBQ是平行四边形 .
∴ 四边形APBQ是平行四边形 .
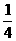 ∴ S△POA = S平行四边形APBQ = ×24 = 6 .
∴ S△POA = S平行四边形APBQ = ×24 = 6 .
设点P的横坐标为 (
( > 0且
> 0且 ),
),

 得P (
得P (  , ) .
, ) .
过点P、A分别做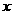 轴的垂线,垂足为E、F,
轴的垂线,垂足为E、F,
∵ 点P、A在双曲线上,∴S△POE = S△AOF = 4 .
若0< <4,如图12-3,
<4,如图12-3,
∵ S△POE + S梯形PEFA = S△POA + S△AOF,
∴ S梯形PEFA = S△POA = 6 .
∴  .
.
解得 = 2,
= 2, = - 8(舍去) .
= - 8(舍去) .
∴ P(2,4).
若  > 4,如图12-4,
> 4,如图12-4,
∵ S△AOF+ S梯形AFEP = S△AOP + S△POE,
∴ S梯形PEFA = S△POA = 6 .
∴ ,
,
解得 = 8,
= 8, = - 2 (舍去) .
= - 2 (舍去) .
∴ P(8,1).
∴ 点P的坐标是P(2,4)或P(8,1).
23、解:张彬的设计方案:
因为P(张彬得到入场券)=  ,
,
P(王华得到入场券)=  ,
,
因为 ,所以,张彬的设计方案不公平.
,所以,张彬的设计方案不公平.
王华的设计方案:
可能出现的的所有结果列表如下:
 第一次 第一次第二次 |
1 |
2 |
3 |
|
1 |
2 |
3 |
4 |
|
2 |
3 |
4 |
5 |
|
3 |
4 |
5 |
6 |
∴P(王华得到入场券)= P(和为偶数)=  ,
,
P(张彬得到入场券)= P(和不是偶数)=  因为
因为 ,
,
所以,王华的设计方案也不公平.
24.证明:(1)∵梯形ABCD为等腰梯形,AB∥CD
∴AD=BC,∠A=∠B
∵AE=BF
∴△ADE≌△BCF
∴∠DEA=∠CFB
∴OE=OF
(2)∵DC∥EF且DC=EF
∴四边形DCEF是平行四边形
又由(1)得△ADE≌△BCF
∴CF=DE
∴四边形DCEF是矩形
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com