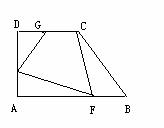
6、如图，在直角梯形ABCD中，∠A=∠D=90°，截取AE=BF=DG=x,已知AB=6，CD=3，AD=4。求：(1)四边形CGEF的面积S关于x的函数表达式和x的取值范围；(2)面积S是否存在着最小值，若存在，求其最小值；若不存在，请说明理由；(3)当x为何值时，S的数值等于x的4倍。 　

3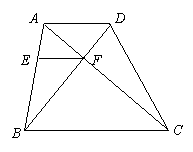．如图，在梯形ABCD中，AD//BC，对角线AC、BD交于点F，点E在AB上，且EF//BC，若AD =3，BC=6，求EF的长.

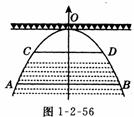
4有一座抛物线形拱桥，在正常水位时水面A B的宽为20m，如果水位上升3米时，水面CD的宽为10m．(1)建立如图1－2－56所示直角坐标系，求此抛物线的解析式；

(2)现有一辆载有救援物质的货车从甲地出发需经过此桥开往乙地，已知甲地距此桥 280km(桥长忽略不计)货车正以 40km／h的速度开往乙地，当行驶1小时，忽然接到通知；前方连降暴雨，造成水位以每小时0．25m的速度持续上涨(货车接到通知时水位在CD处，当水位到达最高点O时，禁止车辆通行)试问：如果货车按原来速度行驶，能否安全通过此桥？若能，请说明理由，若不能，要使货车安全通过此桥，速度应超过每小时多少千米？

5我市长途客运站每天6：30－7：30开往某市的三辆班车，票价相同，但车的舒适程度不同．小张和小王因事需在这一时段乘车去该市，但不知道三辆车开来的顺序．两人采用不同的乘车方案：小张无论如何决定乘坐开来的第一辆车，而小王则是先观察后上车，当第一辆车开来时，他不上车，而是仔细观察车的舒适状况．若第二辆车的状况比第一辆车好，他就上第二辆车；若第二辆车不如第一辆车，他就上第三辆车．若按这三辆车的舒适程度分为优、中、差三等，请你思考并回答下列问题：(1)三辆车按出现的先后顺序共有几种可能？并写出所有情况(2)请画树状图分析哪种方案乘坐优等车的可能性大？

1、某商场购进一种单价为40元的篮球，如果以单价50元出售，那么每月可售出500个，根据销售经验，售价每提高1元，销售量相应减少10个；

(1)假设销售单价提高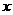元，那么销售每个篮球所获得的利润是　　　　 元；这种篮球每月的销售量是　　　　　 个；(用含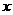的代数式表示)

(2)8000元是否为每月销售这种篮球的最大利润？如果是，请说明理由；如果不是，请求出最大利润，此时篮球的售价应定为多少元？

2在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个，小颖做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：

摸球的次数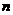	100	200	300	500	800	1000	3000
摸到白球的次数	65	124	178	302	481	599	1803
摸到白球的频率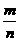	0.65	0.62	0.593	0.604	0.601	0.599	0.601

(1)请估计：当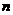很大时，摸到白球的频率将会接近　　　　　 ．(精确到0.1)

(2)假如你摸一次，你摸到白球的概率　　　　 ．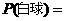

(3)试估算盒子里黑、白两种颜色的球各有多少只？

8.如图，已知BD:CD=2:3,AE:ED=3:4,则AF:FC=　　　　 　　　　　　　　　　　　

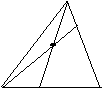　　　 A

　　　　 F　

　　　　　 E　 　　　

　 B　　 D　　　 C

7.一口袋中装有四根长度分别为1cm，3cm，4cm和5cm的细木棒，小明手中有一根长度为3cm的细木棒，现随机从袋内取出两根细木棒与小明手中的细木棒放在一起，回答下列问题：(1)这三根细木棒能构成三角形的概率为　　 　(2)这三根细木棒能构成直角三角形的概率为　　 　　(3)这三根细木棒能构成等腰三角形的概率为　　 　

6.甲、乙两地的实际距离为300千米，甲、乙两地在地图上的距离为3cm，则图上4.5cm的两地之间的实际距离为　　　 千米.

5.十字路口的交通信号灯红灯亮25秒，绿灯亮20秒，黄灯亮15秒，当你抬头看信号灯时，恰好是黄灯的概率是__________________．

4.把一个小球以20 m/s的速度竖直向上弹出，它在空中的高度h(m)与时间t(s)满足关系：h=20t－5t².当h=20 m时，小球的运动时间为　　　

3.已知x∶y∶z= 3∶4∶5 , 且x+y+z=12,　 那么x=　　　 ，y=　　　 ，z=　　　 .

2.若抛物线y=x²－(2k+1)x+k²+2，与x轴有两个交点，则整数k的最小值是______.