24、解：⑴BG=2AM，AM⊥BG；　　　　　　　　　　　　　　　　　　　　　　 2分

⑵延长AM至K，使MK=AM，连结DK、EK，　　　　　　　　 　　　　　　　3分

得□ADKE，则EK⊥DC，∠EKD=∠EAD，

∴∠KDC=∠GAD，∴∠BAG=∠ADK，　　　　　　　　　　　　　　　　　 4分

易证△ABG≌△DAK，　　　　　　　　　　　　　　　　　　　　　　　 5分

∴BG=2AM，∠DAK=∠ABG，　　　　　　　　　　　　　　　　　　　　 6分

∴AM⊥BG.　　　　　　　　　　　　 　　　　　　　　　　　　　　　7分

⑶画图略；BG=2AM，AM⊥BG；(各1分)　　　　　　　　　　　　　　　 10分

23、解及证明：⑴连结OD，　　　　　　　　　 　　　　　　　　　　　　　　　　1分

∵∠BAC的平分线AD交BC于D，∴∠OAD=∠CAD，又∵∠OAD=∠ODA，

∴∠ODA=∠CDA，∴OD∥AC

∵∠C=90°，∴OD⊥BC，　　　　　　　　　　　　　　　　　　　　　 3分

∴BC是⊙O的切线.　　　　　　　　　　　　　　　 　　　　　　　　　4分

⑵∵AC=6，BC=8，∴AB=10，过C作CH⊥AB于H，则CH=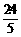，　　　　　 5分

连结OC，设⊙O的半径为r，则S_△ABC=S_△OBC+S_△OAC=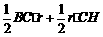　　　 6分

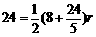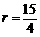∴，∴.　　　　　　　　　　　　　 　　　　　　　8分

22、解：依题意，设金色纸边的宽为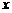cm.　　　　 　　　　　　　　　　　　　　　1分

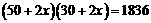　　　　 　　　　　　　　　　　　　　　3分

解之得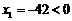：(不合题意，舍去)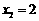，　　　　　　　　　　　　　 　7分

答：金色纸边的宽为2cm.　　　　　　　　　　　　　　 　　　　　　　　　　8分

21、解：⑴一共有5种不同的结果，　　　　　　 　　　　　　　　　　　　　　　　1分

每种结果出现的可能性相等，　　　　　　 　　　　　　　　　　　　　　　2分

满足要求的结果有2种。记事件为A，则P(A)=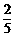.　　　　　　　　　　 　4分

⑵依题意，有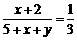：　　　　　　　　 　　　　　　　　　　　　　　　6分

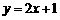∴.　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　8分

20、解及证：设铁环的圆心为O，连结OP、OA，　　　　　　　　　　　　　　　 1分

在Rt△OPA中，PA=5，∠POA=30°，　　　　　　　　　　　　　　 　5分

∴OP=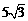(cm)即铁环的半径为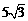cm.　　　　　　　　　　　　　　　 7分

19、解：⑴(画图略)找对一个点坐标给1分　　　　　　　　　 　　　　　　　　3分

⑵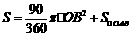=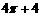(平方单位)　　 　　　　　　　　　　　4分

18、解：原式=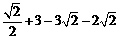　　　 　　　　　　　　　　　　　　　　　　　　3分

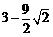=　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

17、解一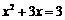：　　　　　　　　　　 解二：a=1，b=3，c=-3；　　　　　 　1分

　　　　　　　　 ∵

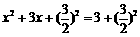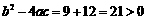
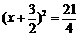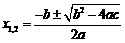　 　　　　　　　　　　∴=　　 　3分

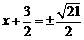
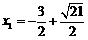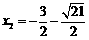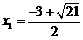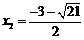　　 ∴，　　　 ∴，　　　　 6分

13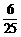．；　　　 14．54；　　　　 15．72；　　　　　　 16．3；

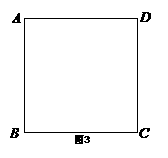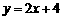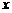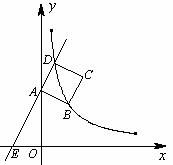
25、(本小题12分)已知，如图，直线与轴交于点E，与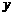轴交于点A，点D是直线AE在第一象限上的一点，以AD为边，在第一象限内做正方形ABCD.

⑴若AD=AE，试求点B的坐标；(3分)

⑵若点B、D恰好在反比例函数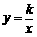上，求反比例函数的解析式；(5分)

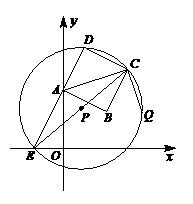⑶经过D、C、E三点作⊙P，过点C作CQ⊥AC交⊙P于Q，当D点在EA延长线上运动时，CQ的长度是否发生变化？若不变，请你证明并求出其值；若变化，请说明理由，并指出其变化范围.(4分)

九年级数学月考答案及评分标准