
题目列表(包括答案和解析)
26. (8分)已知∠AOB=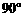 ,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA、OB(或它们的反向延长线)相交于点D、E.
,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA、OB(或它们的反向延长线)相交于点D、E.
当三角板绕点C旋转到CD与OA垂直时(图①),易证:OD+OE=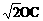
当三角板绕点C旋转到CD与OA不垂直时,在图②、图③这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段OD、OE、OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
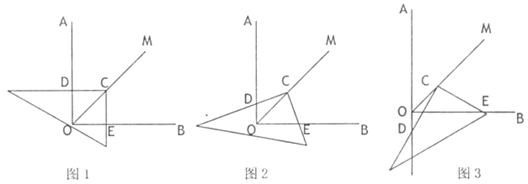
25. (8分)某工厂生产的某种产品按质量分为10个档次,生产第一档次(即最低档次)的产品一天生产76件,每件利润10元,每提高一个档次,利润每件增加2元.
(1)当每件利润为16元时,此产品质量在第几档次?
(2)由于生产工序不同,此产品每提高一个档次,一天产量减少4件,若生产第x档的产品一天的总利润为y元(其中x为正整数,且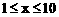 ),求出y关于x的函数关系式;
),求出y关于x的函数关系式;
(3)若生产某档次产品一天的总利润为1080元,该工厂生产的是第几档次的产品?
24. (6分)已知关于x的方程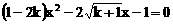 有实数根,求k的取值范围.
有实数根,求k的取值范围.
23. (6分)如图,网格中的图案是美国总统Garfield于1876年给出的一种验证某个著名结论的方法:
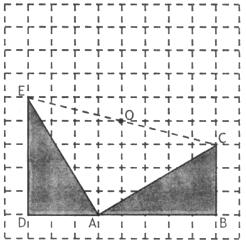
(1)请你画出直角梯形EDBC绕EC中点O顺时针方向旋转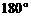 的图案,你会得到一个美丽的图案.(阴影部分不要涂错).
的图案,你会得到一个美丽的图案.(阴影部分不要涂错).
(2)若网格中每个小正方形边长为单位1,旋转后A、B、D的对应点为A′、B′、D′,求四边形ACA′E的面积?
(3)根据旋转前后形成的这个美丽图案,你能说出这个著名的结论吗?若能,请你写出这个结论.
22. (6分)先化简,再求值: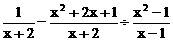 ,其中
,其中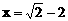
21. (6分)计算 .
.
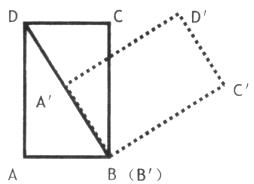
20. 如图,在计算机白色屏幕上有一个矩形画刷ABCD,它的边AB=1,AD=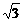 ,以B点为中心,按顺时针方向转动到A′B′C′D′的位置(A′点在对角线BD上),则被这个画刷所着色的面积为(注解:所谓画刷,是屏幕上的一个矩形块,它在屏幕上移动或转动时,它扫过的部位将改变颜色.)
,以B点为中心,按顺时针方向转动到A′B′C′D′的位置(A′点在对角线BD上),则被这个画刷所着色的面积为(注解:所谓画刷,是屏幕上的一个矩形块,它在屏幕上移动或转动时,它扫过的部位将改变颜色.)
A. 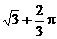 B.
B. 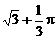 C.
C. 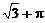 D.
D. 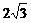
19. 已知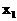 、
、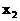 是一元二次方程
是一元二次方程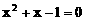 两个实数根,则
两个实数根,则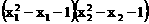 的值为
的值为
A. 0 B. 4 C. –1 D. –4
18. 某种病毒在其生长过程中,在保证自身稳定性的前提下,每隔半小时繁衍若干个新的病毒,如果最初的一个病毒经过1个小时后变成了这样的病毒121个,那么,一个病毒每隔半小时繁衍( )个病毒.
A. 12 B. 11 C. 10 D. 9
17. 如果非零实数满足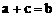 ,则有一根为-1的方程是
,则有一根为-1的方程是
A. 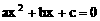 B.
B. 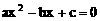
C. 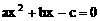 D.
D. 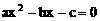
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com