
题目列表(包括答案和解析)
8. 如图,E为正方形ABCD内一点,EC=1,将ΔDEC绕C点按逆时针方向旋转
如图,E为正方形ABCD内一点,EC=1,将ΔDEC绕C点按逆时针方向旋转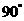 得到ΔBFC,则EF的长为(
)
得到ΔBFC,则EF的长为(
)
A.1
B.2
C.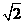
D.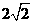
7. 有以下图形:平行四边形、矩形、等腰三角形、线段、菱形,其中既是轴对
称图形又是中心对称图形的有( )
A.5个 B.4个 C.3个 D.2个
6.若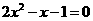 ,则
,则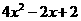 等于( )
等于( )
A.1 B.2 C.3 D.4
5.用配方法将关于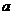 的一元二次方程
的一元二次方程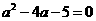 变形得( )
变形得( )
A.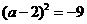 B.
B.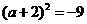
C.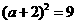 D.
D.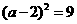
4.已知 和
和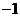 都是某个一元二次方程的根,此方程是( )
都是某个一元二次方程的根,此方程是( )
A.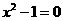 B.
B.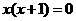
C.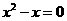 D.
D.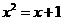
3.某次球赛共有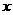 个队参加,每两个队之间打一场比赛,共打了
个队参加,每两个队之间打一场比赛,共打了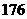 场,则根
场,则根
据题意可列出的方程是( )
A.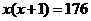 B.
B.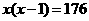
C.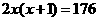 D.
D.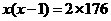
2.一元二次方程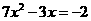 ,其中二次项系数,一次项系数,常数项都正确的是( )
,其中二次项系数,一次项系数,常数项都正确的是( )
A,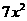 ,
,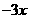 ,
,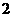 B.
B.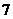 ,
,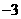 ,
,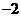
C.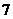 ,
,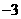 ,
,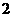 D.
D.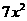 ,
,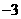 ,
,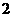
1.关于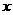 的方程
的方程 是一元二次方程,则( )
是一元二次方程,则( )
A.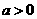 B.
B.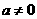 C.
C.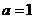 D.
D.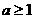
28. (10分)如图,Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点C在y轴上,OA和OC是方程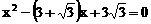 的两根(OA>OC),∠CAO=
的两根(OA>OC),∠CAO=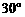 ,将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
,将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
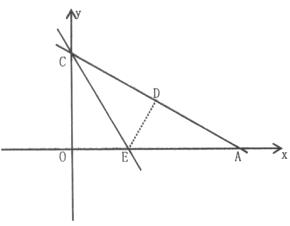
(1)求线段OA和OC的长;
(2)求点D的坐标;
(3)设点M为直线CE上的一点,过点M作AC的平行线,交y轴于点N,是否存在这样的点M,使得以M、N、D、C为顶点的四边形是平行四边形?若存在,请求出符合条件的点M的坐标;若不存在,请说明理由.
27. (10分)某人将一条长为56米的竹篱笆分成两段,并用每段都围成一块正方形的菜地.
(1)要想围成的两块正方形的菜地面积之和为100平方米,该怎样分?
(2)要想围成的两块正方形的菜地面积之和为200平方米,可能吗?
(3)两块正方形的菜地面积之和为最小,该怎样分?
(4)两块正方形的菜地面积之和能否达到90平方米?如能,该怎样分?如不能,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com