
题目列表(包括答案和解析)
1.B 2.D 3.D 4.C 5.A 6.B 7.D 8.B 9.B 10.D
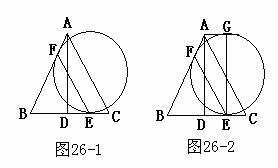
26.(共8分)(08年广安课改)如图26-1,在等边△ABC中,AD⊥BC于点D,一个直径与AD相等的圆与BC相切于点E,与AB相切于点F,连接EF。
(1)判断EF与AC的位置关系(不必说明理由);
(2)如图26-2,过E作BC的垂线,交圆于G,连接AC,判断四边形ADEG的形状,并说明理由。
(3)确定圆心O的位置,并说明理由。
九年级上册综合测试题
25.(自编题) (8分)探究下表中的奥妙,填空并完成下列题目
|
一元二次方程 |
两个根 |
二次三项式因式分解 |
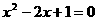 |
 |
 |
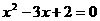 |
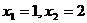 |
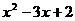  |
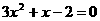 |
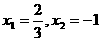 |
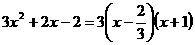 |
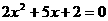 |
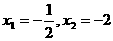 |
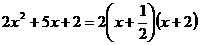 |
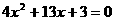 |
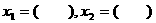 |
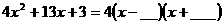 |
(1).如果一元二次方程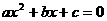 (
(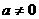 )有解为
)有解为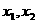 ,请你把二次三项式
,请你把二次三项式 因式分解。
因式分解。
(2).利用上面的结论,把二次三项式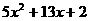 因式分解。
因式分解。
答案:解: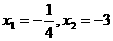
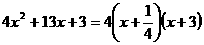
(1). 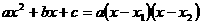
(2). 解方程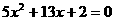 得
得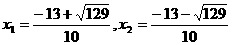
所以 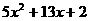 =
=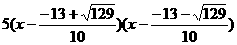
24.(本题6分)如图,⊙I为△ABC的内切圆,AB=9,BC=8,CA=10,点D,E分别为AB,AC上的点,且DE为⊙I的切线,
求△ADE的周长。
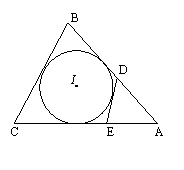


答案:由切线长定理可得△ADE周长为9
23.(8分)如图,某海军基地位于A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C,小岛D位于AC的中点,岛上有一补给码头:小岛F位于BC上且恰好处于小岛D的正南方向,一艘军舰从A出发,经B到C匀速巡航,一般补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
(1)小岛D和小岛F相距多少海里?
(2)已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)
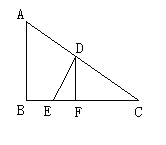
答
案: 解:(1)连结DF,则DF⊥BC
∵AB⊥BC,AB=BC=200海里.
∴AC=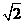 AB=200
AB=200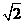 海里,∠C=45°
海里,∠C=45°
∴CD=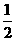 AC=100
AC=100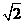 海里
海里
DF=CF,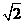 DF=CD
DF=CD
∴DF=CF=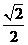 CD=
CD=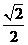 ×100
×100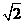 =100(海里)
=100(海里)
所以,小岛D和小岛F相距100海里.
(2)设相遇时补给船航行了x海里,那么DE=x海里,AB+BE=2x海里,
EF=AB+BC-(AB+BE)-CF=(300-2x)海里
在Rt△DEF中,根据勾股定理可得方程
x2=1002+(300-2x)2
整理,得3x2-1200x+100000=0
解这个方程,得:x1=200-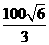 ≈118.4
≈118.4
22.(共6分)(08义乌)“一方有难,八方支援”.四川汶川大地震牵动着全国人民的心,我市某医院准备从甲、乙、丙三位医生和A、B两名护士中选取一位医生和一名护士支援汶川.
(1)若随机选一位医生和一名护士,用树状图(或列表法)表示所有可能出现的结果;
(2)求恰好选中医生甲和护士A的概率.
答案:解:(1)用列表法或树状图表示所有可能结果如下分
(1)列表法: (2)树状图:
|
|
A |
B |
|
甲 |
(甲, A) |
(甲, B) |
|
乙 |
(乙, A) |
(乙, B) |
|
丙 |
(丙, A) |
(丙, B) |
(2)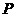 (恰好选中医生甲和护士A)=
(恰好选中医生甲和护士A)=
∴恰好选中医生甲和护士A的概率是
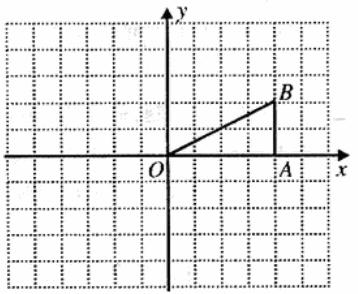
21.(共6分)(08年福州)如图,在 中,
中,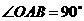 ,且点
,且点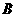 的坐标为(4,2).
的坐标为(4,2).
①画出 向下平移3个单位后的
向下平移3个单位后的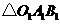 ;
;
②画出 绕点
绕点 逆时针旋转
逆时针旋转 后的
后的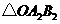 ,并求点
,并求点 旋转到点
旋转到点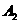 所经过的路线长(结果保留
所经过的路线长(结果保留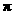 ).
).
答案:解:(1)图略;
(2)图略.点A旋转到点A2所经过的路线长=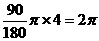
20.解方程(共8分)
①  (用公式法解)
②
(用公式法解)
② 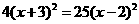
答案:20、①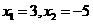 ②
②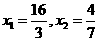
19.计算(共8分)
①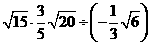 ;
②
;
② 
答案:解:(1)原式=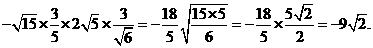
(2)原式=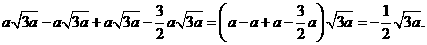
18.矩形ABCD中,AB=5,CD=12.如果分别以A、C为圆心的两圆相切,点D在⊙C内,点B在⊙C外。则⊙A的半径r的取值范围是________。
答案:1∠r∠8 ,18∠r∠25.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com