
题目列表(包括答案和解析)
5、如图,⊙O的直径CD过弦EF的中点G,∠EOD=50°, ∠DCF等于( )
A.80° B. 50° C. 40° D. 25°
4. 已知关于x 的一元二次方程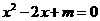 有两个不相等的实数根,则m的取值范围是( ) .
有两个不相等的实数根,则m的取值范围是( ) .
 A. m=1 B. m<1
A. m=1 B. m<1
C. m>1 D.无法判断
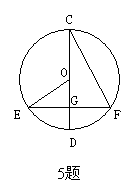
2.下列方程属于一元二次方程的是( )
(A)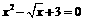 (B)
(B)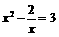
(C)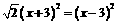 (D)
(D)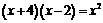
 3 下列图案中,不是中心对称图形的是 ( )
3 下列图案中,不是中心对称图形的是 ( )
1.下列各式中属于最简二次根式的是 ( )
(A)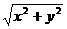 (B)
(B)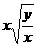 (C)
(C)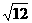 (D)
(D)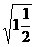
26.解: (1)EF//AC.
(2)四边形ADEG为矩形.
理由: ∵EG⊥BC, ∴AD//EG, 即四边形ADEG为矩形.
(3)圆心O就是AC与EG的交点.
理由: 连接FG, 由(2)可知EG为直径, ∴FG⊥EF,
又由(1)可知, EF//AC, ∴AC⊥FG,
又∵四边形ADEG为矩形, ∴EG⊥AG, 则AG是已知圆的切线.
而AB也是已知圆的切线, AF=AG,
∴AC是FG的垂直平分线, 故AC必过圆心,
因此, 圆心O就是AC与EG的交点.
说明: 也可据△AGO≌△AFO进行说理.
答案:解: (1)EF//AC.
(2)四边形ADEG为矩形.
理由: ∵EG⊥BC, ∴AD//EG, 即四边形ADEG为矩形.
(3)圆心O就是AC与EG的交点.
理由: 连接FG, 由(2)可知EG为直径, ∴FG⊥EF,
又由(1)可知, EF//AC, ∴AC⊥FG,
又∵四边形ADEG为矩形, ∴EG⊥AG, 则AG是已知圆的切线.
而AB也是已知圆的切线, AF=AG,
∴AC是FG的垂直平分线, 故AC必过圆心,
因此, 圆心O就是AC与EG的交点.
说明: 也可据△AGO≌△AFO进行说理.
25.解: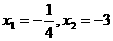
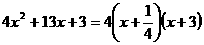
(1). 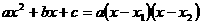
(2). 解方程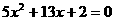 得
得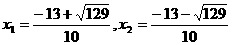
所以
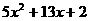 =
=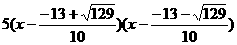
24.由切线长定理可得△ADE周长为9
23.解:(1)连结DF,则DF⊥BC
∵AB⊥BC,AB=BC=200海里.
∴AC=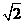 AB=200
AB=200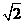 海里,∠C=45°
海里,∠C=45°
∴CD=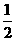 AC=100
AC=100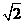 海里
海里
DF=CF,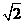 DF=CD
DF=CD
∴DF=CF=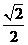 CD=
CD=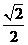 ×100
×100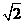 =100(海里)
=100(海里)
所以,小岛D和小岛F相距100海里.
(2)设相遇时补给船航行了x海里,那么DE=x海里,AB+BE=2x海里,
EF=AB+BC-(AB+BE)-CF=(300-2x)海里
在Rt△DEF中,根据勾股定理可得方程
x2=1002+(300-2x)2
整理,得3x2-1200x+100000=0
解这个方程,得:x1=200-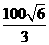 ≈118.4
≈118.4
22.解:(1)用列表法或树状图表示所有可能结果如下分
 (1)列表法:
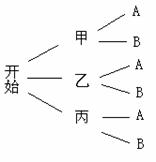
(2)树状图:
(1)列表法:
(2)树状图:
 |
A |
B |
|
甲 |
(甲, A) |
(甲, B) |
|
乙 |
(乙, A) |
(乙, B) |
|
丙 |
(丙, A) |
(丙, B) |
(2)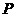 (恰好选中医生甲和护士A)=
(恰好选中医生甲和护士A)=
∴恰好选中医生甲和护士A的概率是
21.解:(1)图略;
(2)图略.点A旋转到点A2所经过的路线长=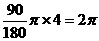
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com