26.(本题12分)解：①将点A(-1,0), B(3,0)代入y=x²+bx+c中得：

…………………………………..1分

解得：…………………………………..3分

　　　　 ②解:设p点的纵坐标为t

∵=1/2×AB×|t|=8　　　　　　　　　　　　　　　　　　　　　　

又∵AB=|3-(-1)|=4 ……….4分

　∴|t|=4 ∴当t=4时x²-2x-3=4 解得x=12

　当t=-4时x²-2x-3=-4 解得x=8…………7分

∴点p坐标为：(1,-4).( 12,4)……………….8分

③存在…………………9分

∵点A,B关于抛物线的对称轴对称∴连接BC与对称轴的交点Q就能使

周长最小…………………………………….10分

设直线BC解析式为：y=kx+b,又∵C(0,-3) B(3,0)

∴解得　　 ∴y=x-3……………………12分

又∵抛物线对称轴为x=1　 ∴Q(1,-2)……………………….13分

25.(本题10分)(1)设一年中这个村修建了x公顷蔬菜大棚, ………1分

则75000x-(27000+9000x²)=60000………2分

解得:x=2或………4分

答: 一年中这个村修建了2或公顷蔬菜大棚………5分

(2)、设一年中这个村修建了x公顷蔬菜大棚,则修建蔬菜大棚而增加的收益(扣除修建费用后)为75000x-(27000+9000x²)元. ………6分

∵75000x-(27000+9000x²)=-9000(x-)²+64000………8分

∴当x=时,75000x-(27000+9000x²)的值最大为64000元………9分

答 :这个村一年中应修建公顷大棚，收益达到最大64000元。………10分

24.(本题10分)(1)(数状图或列表略)

　 方案A： P(和为奇数)==；P(和为偶数)==--------------------2分

　　 方案B： P(和是3的整数倍)==；P(和不是3的整数倍)=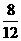=---------4分

　　 方案C： P(和是大于3的数)==；P(和不是大于 3的数)==---------6 分

所以，我选择方案C，并且猜“和是大于3的数”，此时获胜的概率为，最大。

　 (2)为了保证游戏的公平性，应该选择方案A，此时双方获胜的机会一样。----------9分

　 (3)答案不唯一。例如：猜“是大于4的数”或“不是大于 4的数”等。----------12分

23.(本题9分)(1)、画图(如图)A₁(1，-3)、B₁(5，0)、C₁(5，-3)．………3分

(2)、画图(如图)A₂(-1，1)、B₂(-4，5)、C₂(-1，5)………6分

(2)、画图(如图)A₃(7，5)、B₃(3，5)、C₃(3，5)………9分

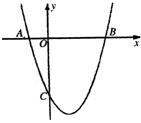
26．(本题12)如图，抛物线与x轴交于A(－1，0)、B(3，0)两点。

　　 　(1)求该抛物线的解析式；(3分)

　　 　(2)设(1)中的抛物线上有一个动点P，当点P在该抛物线上滑动到什么位置时，满足S_△PAB=8，并求出此时P点的坐标；(5分)

　 　　 　(3)设(1)中的抛物线交y轴于C点。在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小，若存在，求出Q点的坐标；若不存在，请说明理由。(5分)

部分答案

25.(本题10分)某村为增加蔬菜的种植面积,一年中修建了一些蔬菜大棚.平均修建每公顷大棚要用的支架、塑料膜等材料的费用为27000元,此外还要购置喷灌设备,这项费用(元)与大棚面积(公顷)的平方成正比,比例系数为9000.每公顷大棚的年平均经济收益为75000元,这个村一年中由于修建蔬菜大棚而增加的收益(扣除修建费用后)为60000元.

(1).一年中这个村修建了多少公顷蔬菜大棚?(5分)

(2).若要使收益达到最大,请问应修建多少公顷大棚?并说明理由.(5分)

23．(本题9分)

如图，已知的顶点的坐标分别是A(-1，-1)B(-5，-4)C(-5，-1)．

(1)、作出关于点P(0,-2)中心对称的图形，

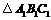并直接写出顶点A₁、B₁、C₁的坐标．(3分)

(2)、将绕原点O按顺时针方向旋转90°后得到△A₂B₂C₂，

画出△A₂B₂C₂，并直接写出顶点A₂、B₂、C₂的坐标．(3分)

(3)、将沿线段BA方向平移10个单位后得到△A₃B₃C₃,

并直接写出顶点A₃、B₃、C₃的坐标．(3分)

22.计算(本题8分)：

先化简，再求值：，其中x ＝2 +

21.解方程：(每小题 5分，共10分)

(1).　　　　　　　　　　　 (2).