
题目列表(包括答案和解析)
23.已知:如图,△ABC中,点O是AC上边上一个动点,过点O作直线MN∥BC,
MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证EO=FO.
(2)当点O运动到何处时,四边形AECF是矩形?证明你的结论.
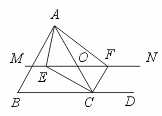
[提示](1)证明OE=OC=OF;
(2)O点的位置首先满足四边形AECF是平行四边形,然后证明它此时也是矩形.
[答案](1)∵ CE平分∠BCA,
∴ ∠BCE=∠ECO.
又 MN∥BC,
∴ ∠BCE=∠CEO.
∴ ∠ECO=∠CEO.
∴ OE=OC.
同理 OC=OF.
∴ OE=OF.
(2)当点O运动到AC边的中点时,四边形AECF是矩形,证明如下:
∵ OE=OF,又O是AC的中点,
即 OA=OC,
∴ 四边形AECF是平行四边形.
∵ CE、CF分别平分∠BCA、∠ACD,且∠BCA+∠ACD=180°,
∴ ∠ECF=∠ECO+∠OCF=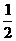 (∠BCA+∠ACD)=90°.
(∠BCA+∠ACD)=90°.
∴ □AECF是矩形.
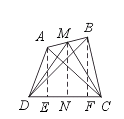
22.如图(1),AB、CD是两条线段,M是AB的中点,S△DMC、S△DAC和S△DBC分别
表示△DMC、△DAC、△DBC的面积.当AB∥CD时,有
S△DMC=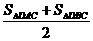 ①
①
 (1)如图(2),若图(1)中AB∥CD时,①式是否成立?请说明理由.
(1)如图(2),若图(1)中AB∥CD时,①式是否成立?请说明理由.
(2)如图(3),若图(1)中AB与CD相交于点O时,S△DMC与S△DAC和S△DBC有何种相等关系?证明你的结论.

图(1) 图(2) 图(3)
[提示]△DAC,△DMC 和△DBC 同底CD,通过它们在CD 边上的高的关系,来确定它们面积的关系.
 [答案](1)当AB∥CD时,①式仍成立.
[答案](1)当AB∥CD时,①式仍成立.
分别过A、M、B作CD的垂线,AE、MN、BF的垂足分别为E、N、F.
∵ M为AB的中点,
∴ MN=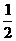 (AE+BF).
(AE+BF).
∴ S△DAC+S△DBC=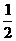 DC·AE+
DC·AE+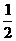 DC·BF=
DC·BF=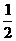 DC·(AE+BF)=2 S△DMC.
DC·(AE+BF)=2 S△DMC.
 ∴ S△DMC=
∴ S△DMC=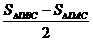
(2)对于图(3)有S△DMC=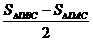 .
.
证法一:∵ M是AB的中点,S△ADM=S△BDM,S△ACM=S△BCM,
S△DBC=S△BDM+S△BCM+S△DMC, ①
S△DAC=S△ADM+S△ACM-S△DMC ②
 ①-②得:S△DBC-S△DAC=2 S△DMC
①-②得:S△DBC-S△DAC=2 S△DMC
∴ S△DMC=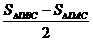 .
.
证法二:如右图,过A作CD的平行线l,MN⊥l,垂足为N,BE⊥l,垂足为E.设A、M、B到CD的距离分别h1、h0、h2.则MN=h1+h0,BE=h2+h1.
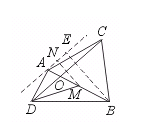
∵ AM=BM,
∴ BE=2 MN.
∴ h2+h1=2(h1+h0),
∴ h0=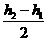 .
.
∴ S△DMC=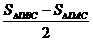 .
.
21.如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN为定角a,
连结AM、AN,并延长分别交BC、CD于E、F两点,则∠CME与∠CNF在M、
N两点移动过程,它们的和是否有变化?证明你的结论.
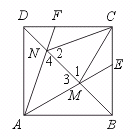
[提示]BD为正方形ABCD的对称轴,
∴ ∠1=∠3,∠2=∠4,
用∠1和∠2表示∠MCN以及∠EMC+∠FNC.
[答案]∵ BD为正方形ABCD的对称轴,
∴ ∠1=∠3,∠2=∠4,
∴ ∠EMC=180°-∠1-∠3=180°-2∠1.
同理 ∠FNC=180°-2∠2.
∴ ∠EMC+∠FNC=360°-2(∠1+∠2).
∵ ∠MCN=180°-(∠1+∠2),
∴ ∠EMC+∠FNC总与2∠MCN相等.
因此∠EMC+∠FNC始终为定角,这定角为∠MCN的2倍.
20.已知:如图,以正方形ABCD的对角线为边作菱形AEFC,B在FE的延长线上.
求证:AE、AF把∠BAC三等分.
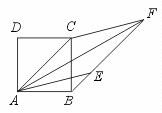
[提示]证出∠CAE=30°即可.
[答案]连结BD,交AC于点O,作EG⊥AC,垂足为G点.
∵ 四边形AEFC为菱形,
∴ EF∥AC.
 ∴ GE=OB.
∴ GE=OB.
∵ 四边形ABCD为正方形,
∴ OB⊥AC,
∴ OB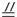 GE,
GE,
∵ AE=AC,OB=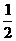 BD=
BD=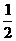 AC,
AC,
∴ EG=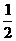 AE,
AE,
∴ ∠EAG=30°.
∴ ∠BAE=15°.
在菱形AEFC中,AF平分∠EAC,
∴ ∠EAF=∠FAC=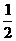 ∠EAC=15°
∠EAC=15°
∴ ∠EAB=∠FAE=∠FAC.
即AE、AF将∠BAC三等分.
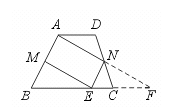
19.如图,在梯形ABCD中,AD∥BC,M、N分别是AB、CD的中点,ME∥AN交BC于点E,求证AM=NE.
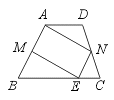
[提示]延长AN交BC延长线于点F.证明NE为△ABF的中位线.
[答案]延长AN交BC的延长线于点F,
 ∵ DN=CN,∠AND=FNC,
∵ DN=CN,∠AND=FNC,
又由AD∥BC,得∠ADN=∠FCN,
∴ △ADN≌△FCN.
∴ AN=NF.
∵ AM=BM且ME∥AF,
∴ BE=EF.
∴ NE为△ABF的中位线,
∴ NE=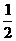 AB=AM.
AB=AM.
18.如图,E是矩形ABCD的边AD上一点,且BE=ED,P是对角线BD上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.求证:PF+PG=AB.

[提示]延长GP交BC于H,只要证PH=PF即可,所以只要证∠PBF=∠PBH.
[答案]∵ BE=DE,
∴ ∠EBD=∠EDB.
 ∵ 在矩形ABCD中,AD∥BC,
∵ 在矩形ABCD中,AD∥BC,
∴ ∠DBC=∠ADB,
∴ ∠EBD=∠CBD.
延长GP交BC于H点.
∵ PG⊥AD,
∴ PH⊥BC.
∵ PF⊥BE,P是∠EBC的平分线上.
∴ PF=PH.
∵ 四边形ABHG中,
∠A=∠ABH=∠BHG=∠HGA=90°.
∴ 四边形ABHG为矩形,
∴ AB=GH=GP+PH=GP+PF
故 PF+PG=AB.
17.已知:如图,梯形ABCD中,AD∥BC,过C作CE∥AB且CE=AB,连结
DE交BC于F.求证:DF=EF.
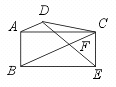
[提示]连结AE交BC于O,要证DF=EF,因为AD∥BC,所以只要证OA=OE,只要证四边形ABEC为平行四边形.
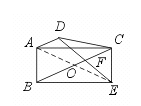 [答案]连结AE交BC于O点,
[答案]连结AE交BC于O点,
∵ CE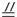 AB,
AB,
∴ 四边形ABEC为平行四边形,
∴ OA=OE.
又 AD∥BC,
∴ DF=EF.
16.如图,矩形纸片ABCD中,AB=3 cm,BC=4 cm.现将A,C重合,使纸片
折叠压平,设折痕为EF,试求AF的长和重叠部分△AEF的面积.
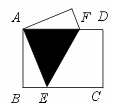
[提示]把AF取作△AEF的底,AF边上的高等于AB=3.
由折叠过程知,EF经过矩形的对称中心,FD=BE,AE=CE=AF.由此可以在
△ABE中使用勾股定理求AE,即求得AF的长.
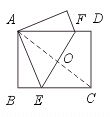
[答案]如图,连结AC,交EF于点O,
由折叠过程可知,OA=OC,
∴ O点为矩形的对称中心.E、F关于O点对称,B、D也关于O点对称.
∴ BE=FD,EC=AF,
 由EC折叠后与EA重合,
由EC折叠后与EA重合,
∴ EC=EA.
设AF=x,则BE=FD=AD-AF=4-x,AE=AF=x.
在Rt△ABE中,由勾股定理,得
AB2+BE2=AE2,即 32+(4-x) 2=x2.
解得 x=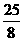 .
.
∴ S△AEF=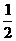 ×3×
×3×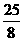 =
=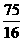 (cm2)
(cm2)
故AF的长为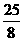 cm,△AEF的面积为
cm,△AEF的面积为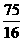 cm2.
cm2.
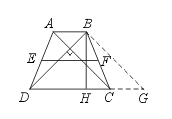
15.如图,一个等腰梯形的两条对角线互相垂直,且中位线长为l,求这个等腰梯形的高.
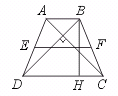
[提示]如下图,过B点作AC的平行线.
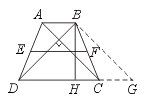
[答案]过B作BG∥AC,交DC的延长线于G点.
在梯形ABCD中,AB∥DC,
 ∴ 四边形ABGC为平行四边形.
∴ 四边形ABGC为平行四边形.
∴ CG=AB,BG=AC.
∵ EF为梯形中位线,
∴ DG=DC+AB=2 EF=2 l.
∵ AC⊥BD且AC=BD.
∴ BG⊥BD且BG=BD.
∴ △BDG为等腰直角三角形.
∴ 高BH=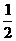 DG=l.
DG=l.
13. [答案]55.
14. [答案]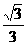 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com