24．如图，在梯形ABCD中，AD∥BC，AB＝DC，BD⊥DC于D，且∠C＝60°，若

AD＝5 cm，求梯形的腰长．

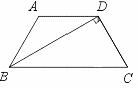
[提示]求出∠CBD，∠ABD和∠ADC的度数，证明AB＝AD，或者过D点作DE⊥BC于E，CE为下底与上底的差的一半，又是CD的一半，CD又是BC的一半．从中找出CD与AD的关系．

[解法一]∵　 BD⊥CD，∠C＝60°，

∴　 ∠CBD＝30°．

在等腰梯形ABCD中，∠ABC＝∠C＝60°，

∴　 ∠ABD＝∠CBD＝30°．

∵　 AD∥BC，

∴　 ∠ADB＝∠CBD．

∴　 ∠ABD＝∠ADB．

∴　 AB＝AD＝5(cm)．

[解法二]过D点作DE⊥BC，垂足为E点．

∵　 在Rt△CDE中，∠CDE＝30°，

∴　 CE＝CD．

又　 CE＝(BC－AD)，

∴　 CD＝BC－AD．

即　 BC＝CD+AD．

又 在Rt△BCD中，∠CBD＝30°，

∴　 CD＝BC．

∴　 CD＝2 CD－AD．

即　 CD＝AD＝5(cm)．

23．已知：如图，在□ABCD中，BE、CE分别平分∠ABC、∠BCD，E在AD上，

BE＝12 cm，CE＝5 cm．求□ABCD的周长和面积．

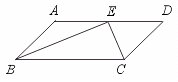
[提示]证明BE⊥EC和E为AD中点．

[答案]在□ABCD中，

∵　 AB∥CD，

∴　 ∠ABC+∠BCD＝180°．

∵　 ∠ABE＝∠EBC，∠BCE＝∠ECD，

∴　 ∠EBC+∠BCE＝(∠ABC+∠BCD)＝90°．

∴　 ∠BEC＝90°．

∴　 BC²＝BE²+CE²＝12²+5²＝13²．

∴　 BC＝13．

∵　 AD∥BC，

∴　 ∠AEB＝∠EBC．

∴　 ∠AEB＝∠ABE．

∴　 AB＝AE．

同理　 CD＝ED．

∵　 AB＝CD，

∴　 AB＝AE＝CD＝ED＝BC＝6.5．

∴　 □ABCD的周长＝2(AB+BC)＝2(6．5+13)＝39．

　 S_□ABCD＝2 S_△BCE＝2·BE·EC

＝12×5＝60．

22．证明等腰梯形判定定理：在同一底上的两个角相等的梯形是等腰梯形．(要求：画出

图形，写出已知、求证、证明．)

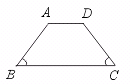
[提示]作辅助线，构造等腰三角形．

[答案]已知：在梯形ABCD中，AD∥BC，∠B＝∠C(图(1))．求证：AB＝DC．

[证法一]如图(1)，过点D作DE∥AB，交BC于E．

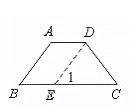
图(1)　　

∴　 ∠B＝∠1．又　 ∠B＝∠C，∴　 ∠C＝1．

∴　 DE＝DC．又　 AB∥DE，AD∥BE，

∴　 四边形ABED为平行四边形，∴　 AB＝DE．

∴　 AB＝DC．

[证法二]如图(2)，分别延长BA、CD，交于点E．

图(2)　

∵　 ∠B＝∠C，∴　 BE＝CE．

∵　 AD∥BC，∴　 ∠B＝∠1，∠C＝∠2．

∴　 ∠1＝∠2．∴　 AE＝DE．

∴　 BE－AE＝CE－DE，即AB＝DC．

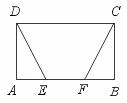
21．已知：如图，矩形ABCD中，E、F是AB上的两点，且AF＝BE．

求证：∠ADE＝∠BCF．

[提示]证明Rt△ADE≌Rt△BCF．

[答案]在矩形ABCD中，

∠A＝∠B＝90°，AD＝BC．

又　 AF＝BE，

∴　 AF－EF＝BE－EF，

即　 AE＝BF．

∴　 Rt△ADE≌Rt△BCF．

∴　 ∠ADE＝∠BCF．

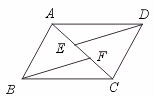
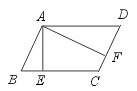
20．已知：如图，AD∥BC，ED∥BF，且AF＝CE．求证：四边形ABCD是平行四边形．

[提示]证明△ADE≌△CBF，得到AD＝BC即可．

[答案]在△ADE和△CBF中，

∵　 AD∥BC，

∴　 ∠DAE＝∠BCF．

∵　 ED∥BF，

∴　 ∠DEF＝∠BFE．

∴　 ∠DEA＝∠BFC．

∵　 AF＝CE，

∴　 AE＝CF．

∴　 △ADE≌△CBF．

∴　 AD＝BC．

又　 AD∥BC，

∴　 四边形ABCD是平行四边形．

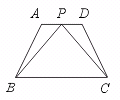
19．已知：如图，在梯形ABCD中，AD∥BC，AB＝DC，P是AD中点．

求证：BP＝PC．

[提示]证明△ABP≌△DCP．

[答案]在梯形ABCD中，AD∥BC，

∵　 AB＝DC，

∴　 ∠A＝∠D．

∵　 P是AD中点，

∴　 AP＝DP．

在△ABP和△DCP中，

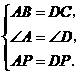
∴　 △ABP≌△DCP．

∴　 PB＝PC．

18．如图，在□ABCD中，AE⊥BC于E，AF⊥CD于F，若AE＝4，AF＝6，□ABCD

的周长为40，则S_□ABCD为______．

[提示]在□ABCD中，AE·BC＝AF·CD＝S_□ABCD，BC+CD＝20，求BC或CD．

[答案]48．

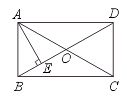
17．如图，矩形ABCD中，O是两对角线的交点AE⊥BD，垂足为E．若OD＝2 OE，

AE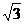＝，则DE的长为______．

[提示]OA＝OD＝2 OE，用勾股定理求出OE和OA的长．

[答案]3．

16．如图，在梯形ABCD中，AD∥BC，中位线EF分别与BD、AC交于点G、H．若

AD＝6，BC＝10，则GH的长是______．

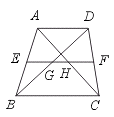
[答案]2．

15．请画出把下列矩形的面积二等分的直线，并填空(一个矩形只画一条直线，不写画

法)．在一个矩形中，把此矩形面积二等分的直线最多有_____条，这些直线都必须经过此矩形的_____点．

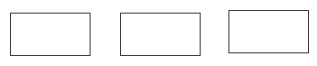
[答案]无数；对称中心(或两条对角线的交点)．