8．在做针尖落地的实验中，正确的是(　　 )

A．甲做了4 000次，得出针尖触地的机会约为46%，于是他断定在做第4 001次时，针尖肯定不会触地

B．乙认为一次一次做，速度太慢，他拿来了大把材料、形状及大小都完全一样的图钉，随意朝上轻轻抛出，然后统计针尖触地的个数，这样大大提高了速度

C．老师安排每位同学回家做实验，图钉自由选取

D．老师安排同学回家做实验，图钉统一发(完全一样的图钉)．同学交来的结果，老师挑选他满意的进行统计，他不满意的就不要

7．在一副(54张)扑克牌中，摸到“A”的频率是(　　 )

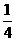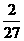A．　　　　　 B．　　　　 C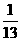．　　　　　 D．无法估计

6．实验的总次数、频数及频率三者的关系是(　　 )

A．频数越大，频率越大

B．频数与总次数成正比

C．总次数一定时，频数越大，频率可达到很大

D．频数一定时，频率与总次数成反比

5．公路上行驶的一辆汽车车牌为偶数的频率约是(　　 )

A．50%　　　　　　　　　　　　　　　　　　　　　　 B．100%

C．由各车所在单位或个人定　　　　　　 D．无法确定

4．抛一枚均匀的硬币100次，若出现正面的次数为45次，那么出现正面的频率是　　　　 ．

3．在红桃A至红桃K这13张扑克牌中，每次抽出一张，然后放回洗牌再抽，研究恰好抽到的数字小于5的牌的概率，若用计算机模拟实验，则要在　　　　 的范围中产生随机数，若产生的随机数是　　　　　 ，则代表“出现小于5”，否则就不是．

2．某灯泡厂在一次质量检查中，从2 000个灯泡中随机抽查了100个，其中有10个不合格，则出现不合格灯泡的频率是　　　 ，在这2 000个灯泡中，估计有　　　 个为不合格产品．

1．通过实验的方法用频率估计概率的大小，必须要求实验是在　　　　　 的条件下进行．

26．已知：如图，在四边形ABCD中，E为AB上一点，△ADE和△BCE都是等边三

角形，AB、BC、CD、DA的中点分别为P、Q、M、N，试判断四边形PQMN为怎样的四边形，并证明你的结论．

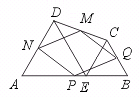
[提示]连结AC和CD，首先利用中位线定理和平行四边形判定定理，证明四边形PQMN为平行四边形，然后证明△AEC≌△DEB，得到AC＝BD，再证明□PQMN为菱形．

[答案]四边形PQMN为菱形．证明如下：

如图，连结AC、BD．

∵　 PQ为△ABC的中位线，

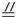
∴　 PQ AC．

同理　 MN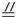AC．

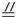∴　 MNPQ，

∴　 四边形PQMN为平行四边形．

在△AEC和△DEB中，

AE＝DE，EC＝EB，∠AED＝60°＝∠CEB，

即　 ∠AEC＝∠DEB．

∴　 △AEC≌△DEB．

∴　 AC＝BD．

∴　 PQ＝AC＝BD＝PN．

∴　 □PQMN为菱形．

25．如图，在正方形ABCD中，点E、F分别在BC、CD上移动，但A到EF的距离

AH始终保持与AB长相等，问在E、F移动过程中：

(1)∠EAF的大小是否有变化？请说明理由．

(2)△ECF的周长是否有变化？请说明理由．

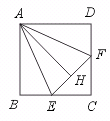
[提示]证明△EAH≌△EAB，△FAH≌△FAD．

[答案](1)∠EAF始终等于45°．证明如下：

在△EAH和△EAB中，

∵　 AH⊥EF，∴　 ∠AHE＝90°＝∠B．

又　 AH＝AB，AE＝AE，∴　 Rt△EAH≌Rt△EAB．

∴　 ∠EAH＝∠EAB．

同理　 ∠HAF＝∠DAF．∴　 ∠EAF＝∠EAH+∠FAH

＝∠EAB+∠FAD＝∠BAD＝45°．

因此，当EF在移动过程中，∠EAF始终为45°角．

(2)△ECF的周长不变．证明如下：

∵　 △EAH≌△EAB，

∴　 EH＝EB．

同理　 FH＝FD．

∴　 △ECF周长＝EC+CF+EH+HF

＝EC+CF+BE+DF

＝BC+CD＝定长．