8．利用函数图象求方程的解是_________．

7．某校运动会上，张强同学推铅球时，铅球行进的高度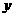(米)与水平距离(米)之间的函数关系式为，张强同学的成绩是_________米．

6．请你写出函数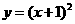与具有的一个共同的性质_________．

5．已知二次函数的图象开口向下，且与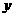轴的正半轴相交，请你写出一个

满足条件的二次函数关系式_________．

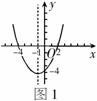
4．已知二次函数的图象如图1所示，则当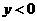时，对应

的取值范围是_________．

3．函数中，当时，相应的函数值为，则．(选填“＜”、“＞”或“＝”)

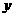2．已知一抛物线和的图象形状相同，对称轴平行于轴，且顶点坐标为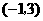，则它所对应的函数关系式为_________．

1．函数的对称轴是_________，顶点坐标是_________，当_______时，函数取得最_________值，值为_________．

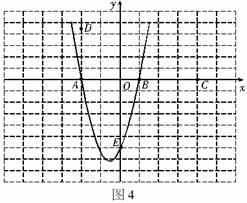
5．(本题15分)在平面直角坐标系中，给定以下五点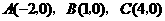，，，从这五点中选取三点，使经过这三点的抛物线满足以平行于轴的直线为对称轴．我们约定：把经过三点的抛物线表示为抛物线(如图4所示)．

(1)问符合条件的抛物线还有哪几条？不求函数关系式，请用约定的方法一一表示出来．

(2)在(1)中是否存在这样的一条抛物线，它与余下的两点所确定的直线不相交？如果存在，试求出抛物线及直线的关系式；如果不存在，请说明理由．

4．(本题14分)某生物兴趣小组在四天的实验研究中发现：骆驼的体温会随外部环境温度的变化而变化，而且在这四天中每昼夜的体温变化情况相同．他们将一头骆驼前两昼夜的体温变化情况绘制成图3，请根据图象回答：

(1)第一天中，在什么时间范围内这头骆驼的体温是上升的？它的体温从最低上升到最高需要多少时间？

(2)第三天12时时这头骆驼的体温是多少？

(3)兴趣小组又在研究中发现，图中10时到22时的曲线是抛物线，求该抛物线所对应的二次函数关系式．