17．(10分)近年来，由于乱砍滥伐，掠夺性使用森林资源，我国长江、黄河流域植被遭到破坏，土地沙化严重，洪涝灾害时有发生．沿黄某地区为积极响应和支持“保护母亲河”的倡议，建造了长100千米，宽0.5千米的防护林．有关部门为掌握这一防护林共约有多少棵树，从中选出10块(每块长1千米，宽0.5千米)进行统计，每块树木数量如下(单位：棵)

65 100　　 63 200　　 64 600　　 64 700　　 67 300

63 300　　 65 100　　 66 600　　 62 800　　 65 500

请你根据以上数据计算这一防护林共约有多少棵树(结果保留3个有效数字)．

[解]先计算出

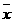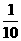＝(65 100+63 200+64 600+64 700+67 300+63 300

+65 100+66 600+62 800+65 500)

＝64 820．

于是，可以估计这一防护林平均每块约有64820株树．又64 820×100＝6 482 000≈6.48×10⁶(株)，于是可以估计这一防护林大约共有6.48×10⁶株树．

[点评]本例一方面要求学生有用样本估计总体的思想方法，另一方面要求学生有应用数学的意识，这是今后中考命题发展的趋势．

16．某班通过一次射击测试，在甲、乙两名同学中选出一名同学代表班级参加校射击比赛．这两位同学在相同条件下各射靶5次，所测得的成绩分别如下(单位：环)：

甲　 9.6　 9.5　 9.3　 9.4　 9.7

乙　 9.3　 9.8　 9.6　 9.3　 9.5

根据测试成绩，你认为应该由__________代表班级参赛．

[提示]比较平均数与方差．

[答案]甲．

15．把容量是64的样本分成8组，从第1组到第4组的频数分别是5，7，11，13，第5组到第7组的频率是0.125，那么第8组的频数是__________，频率是__________．

[提示]64×0.125＝8，故64－5－7－11－13－8×3＝4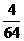，＝0.062 5．

[答案]4，0.062 5．

[点评]注意应用各组频数之和等于样本容量、频率之和为1这两个性质．

14．样本数据－1，2，0，－3，－2，3，1的标准差等于__________．

[提示]s ²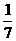＝(1+4+0+9+4+9+1)＝4．

[答案]2．

[点评]求标准差一般先计算出样本方差，再取其算术平方根．

13．某次考试A，B，C，D，E这5名学生的平均分为62分，若学生A 除外，其余学生的平均得分为60分，那么学生A 的得分是__________．

[分析]设A得分为x分，其余4名学生得分的和为60×4＝240分，则240+x＝62×5，x＝70．

[答案]70分．

12．一个班5名学生参加一次演讲比赛，平均得分是89分，有2名学生得87分，两名学生得92分，这组数据的众数是__________．

[提示]设另一名学生得x分，则(92+87)×2+x＝89×5，解得x＝87．

[答案]87．

[点评]本题关键是列方程求得另一名学生的成绩．

11．一批灯泡共有2万个，为了考察这批灯泡的使用寿命，从中抽查了50个灯泡的使用寿命，在这个问题中，总体是__________，样本容量是__________，个体是__________．

[答案]2万个灯泡使用寿命的全体，50，每个灯泡的使用寿命．

[点评]注意样本容量没有单位．

9．已知下列说法：

(1)众数所在的组的频率最大；

(2)各组频数之和为1；

(3)如果一组数据的最大值与最小值的差是15，组距为3，那么这组数据应分为5组；

(4)频率分布直方图中每个小长方形的高与这一组的频数成正比例．

正确的说法是…………………………………………………(　　 )

(A)(1)(3)　　 (B)(2)(3)　　 (C)(3)(4)　　 (D)(4)

[答案]D．

[点评]本题考查与频率分布有关的概念．判断(4)正确，是因为每一个小长方形的高等于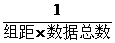＝×频数，故小长方形的高与频数成正比例．

8．抽查了某学校六月份里5天的日用电量，结果如下(单位：kW)．

400　　 410　　 395　　 405　　 390

根据以上数据，估计这所学校六月份的总用电量为……………………(　　 )

(A)12 400 kW　　 (B)12 000 kW　　 (C)2 000 kW　　 (D)400 kW

[提示]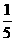(400+410+395+405+390)＝400，故30×400＝12000．

[答案]B．

[点评]本题需用样本平均数估计总体平均数．注意本题要求的是全月的用电量．