
题目列表(包括答案和解析)
5、有甲、乙两种水稻,测得每种水稻各10穴的分孽数后,计算出样本方差分别为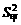 =11,
=11,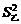 =3.4,由此可以估计( )
=3.4,由此可以估计( )
(A)甲比乙种水稻分蘖整齐 (B)乙种水稻分蘖比甲种水稻整齐
(C)分蘖整齐程度相同 (D)甲、乙两种水稻分孽整齐程度不能比
4、某省有7万名学生参加初中毕业会考,要想了解这7万名学生的数学成绩,从中抽取了1000名考生的数学成绩进行统计分析,以下说法正确的是 ( )
 (A)这1000名考生是总体的一个样本
(A)这1000名考生是总体的一个样本
(B)每位考生的数学成绩是个体
(C)7万名考生是总体
(D)1000名考生是样本容量
3、从一组数据中取出a个x1,b个x2,c个x3,组成一个样本,那么这个样本的平均数是( )。
(A)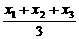 (B)
(B)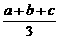 (C)
(C)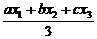 (D)
(D)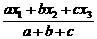
2.在某次数学测验中,随机抽取了10份试卷,其成绩如下:
85,81,89,81,72,82,77,81,79,83.
则这组数据的众数、平均数与中位数分别为 ( )
(A)81,82,81 (B)81,81,76.5
(C)83,81,77 (D)81,81,81
1、某工厂对一个生产小组的零件进行抽样调查。在10天中,这个生产小组每天出的次品数如下(单位:个)
0,2,0,2,3,0,2,3,1,2
在这10天中,该生产小组生产零件所出的次品数为 ( )
(A)平均数是2 (B)众数是3 (C)中位数是1.5 (D)方差是1.2
2.5 x2-10 x-150=0,
即
x2-4 x-60=0.
解得
x1=10,x2=-6.
经检验,x1=10,x2=-6都是原方程的根,但x=-6不合题意,舍去.
故这箱甲种糖果有10千克.
21.(15分)某商店将甲、乙两种糖果混合销售,并按以下公式确定混合糖果的单价:单价=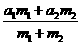 (元/千克),其中m1、m2 分别为甲、乙两种糖果的重量(千克),a1、a2分别为甲、乙两种糖果的单价(元/千克).已知甲种糖果单价为20元/千克,乙种糖果单价为16元/千克.现将10千克乙种糖果和一箱甲种糖果混合(搅拌均匀)销售,售出5千克后,又在混合糖果中加入5千克乙种糖果,再出售时,混合糖果的单价为17.5元/千克.这箱甲种糖果有多少千克?
(元/千克),其中m1、m2 分别为甲、乙两种糖果的重量(千克),a1、a2分别为甲、乙两种糖果的单价(元/千克).已知甲种糖果单价为20元/千克,乙种糖果单价为16元/千克.现将10千克乙种糖果和一箱甲种糖果混合(搅拌均匀)销售,售出5千克后,又在混合糖果中加入5千克乙种糖果,再出售时,混合糖果的单价为17.5元/千克.这箱甲种糖果有多少千克?
[提示]本题要依题意找到其中的等量关系,列出方程以求解.
[解]设这箱甲种糖果有x千克,则有
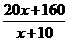 (x+5)+80=17.5(x+10).
(x+5)+80=17.5(x+10).
化简,得
20.(8分)已知数据x1,x2,x3,x4,x5,其中每一个数均为非负整数且互不相等,中位数是2,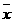 =2.(1)求这组数据;(2)计算这组数据的标准差.
=2.(1)求这组数据;(2)计算这组数据的标准差.
[解](1)因各数据互不相等,不妨设x1<x2<x3<x4<x5,则x3=2,故这组数据为0,1,2,3,4.
(2)s=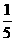 (12+22+32+42+02-5×22)=
(12+22+32+42+02-5×22)=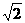 .
.
19.(9分)从甲、乙、丙三个厂家生产的同一种产品中,各抽出8件产品,对其使用寿命进行跟踪调查,结果如下(单位:年)
甲 3 4 5 6 8 8 8 10
乙 4 6 6 6 8 9 12 13
丙 3 3 4 7 9 10 11 12
三家广告中都称这种产品的使用寿命是8年.请根据调查结果判断厂家在广告中分别运用了平均数、众数、中位数中哪一种反映集中趋势的特征数.
[答案]甲:众数 乙:平均数 丙:中位数
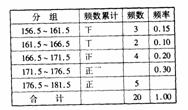
18.(10分)在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5 月1日至30日.评委会把同学们上交作品的件数按5天一组分组统计,绘制了频率分布直方图如下.已知从左至右各长方形的高的比为2∶3∶4∶6∶4∶1,第三组的频数为12,请解答下列问题:
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,这两组哪组获奖率较高?
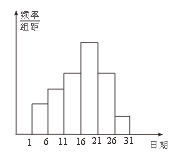
[解](1)依题意,可算出第三组的频率为
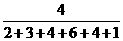 =
=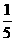 ,
,
然后依据频率= ,知本次活动其参评的作品数=
,知本次活动其参评的作品数=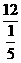 =60(件);
=60(件);
(2)根据频率分布直方图,可看出第四组上交的作品数量最多,共有
 (件);
(件);
(3)易求得第四组获奖率为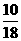 =
= ,
,
第六组获奖率为 =
=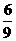 ,
,
由此可知,第六组获奖率较高.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com