
题目列表(包括答案和解析)
25.已知:如图,AD∥EF,∠1=∠2.求证:AB∥DG.
[提示]证明∠BAD=∠2.
[证明]∵ AD∥EF(已知),∴ ∠1=∠BAD(两直线平行,同位角相等).
∵ ∠1=∠2(已知), ∴ ∠BAD=∠2(等量代换).
∴ AB∥DG(内错角相等,两直线平行).
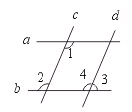
24.如图,a∥b,c∥d,∠1=113°,求∠2、∠3的度数.
[提示]由a∥b,∠1=113°,可求∠2.由c∥d和求出的∠2的度数可求∠4.然而求出∠3.[答案]∠2=113°.∠3=67°.
∵ a∥b(已知).∴ ∠2=∠1=113°(两直线平行,内错角相等).
∵ c∥d(已知).∴ ∠4=∠2=113°(两直线平行,同位角相等).
∵ ∠3+∠4=180°(邻补角定义),∴ ∠3=67°(等式性质).
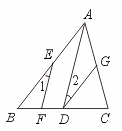
23.如图,∠B=∠D,∠1=∠2.求证:AB∥CD.

(23题) (24题) (25题)
[证明]∵ ∠1=∠2(已知),
∴ ∥ ( ),
∴ ∠DAB+∠ =180°( ).
∵ ∠B=∠D(已知),
∴ ∠DAB+∠ =180°( ),
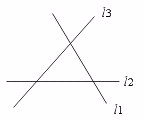
∴ AB∥CD( ).
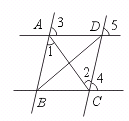
[答案]AD,BC,内错角相等两直线平行;
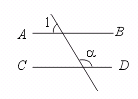
B,两直线平行,同旁内角互补;D,等量代换;同旁内角互补,两直线平行.
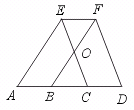
22.如图,∵ ∠ACE=∠D(已知),
∴ ∥ ( ).
∴ ∠ACE=∠FEC(已知),
∴ ∥ ( ).
∵ ∠AEC=∠BOC(已知),
∴ ∥ ( ).
∵ ∠BFD+∠FOC=180°(已知),
∴ ∥ ( ).
[答案]CE,DF,同位角相等,两直线平行;EF,AD,内错角相等,两直线平行;AE、BF,同位角相等,两直线平行;EC,DF,同旁内角互补,两直线平行.
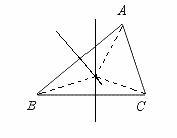
21.如图,分别作出线段AB、BC、的垂直平分线,设交点为O,连结OA、OB、OC.量得OA=( )mm,OB=( )mm,OC=( )mm.则OA、OB、OC的关系是. [答案]18,18,18.OA=OB=OC.
 (22)
(22)
20.如图,AB∥CD.若∠2是∠1的两倍,则∠2等于………………………( )
(A)60° (B)90° (C)120° (D)150°
[提示]由AB∥CD,可得∠3+∠2=180°.
∵ ∠1=∠3, ∴ ∠1+∠2=180°.
∵ ∠2=2∠1, ∴ 3∠1=180°.
∴ ∠1=60°. ∴ ∠2=2×60°=120°. [答案]D.
19.如图,下列推理正确的是………………………………………………( )
(A)∵ ∠1=∠2,∴ AD∥BC (B)∵ ∠3=∠4,∴ AB∥CD
(C)∵ ∠3=∠5,∴ AB∥DC (D)∵ ∠3=∠5,∴ AD∥BC
[答案]C.
18.如图,图中的同位角共有………………………………………………( )
(A)6对 (B)8对 (C)10对 (D)12对
(18题) (19题) (20题)
[提示]可采用17题的方法.
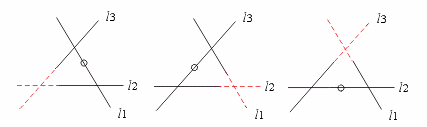
两条直线被第三条直线所截,同位角有四对,图中有三组两条直线被第三条直线所截,均共有同位角4×3=12对. [答案]D.
17.如图,下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是…………………( )
(A)①、②、③ (B)①、②、④ (C)②、③、④ (D)①、②、③、④
[提示]可将涉及的一对角从整个图形中分离出来,单独观察.如
①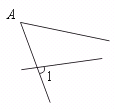 ②
②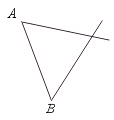 ③
③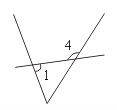 ④
④ 这样可排除图中其它线的干扰,便于确定两角的相对位置.易知①、②、③正确. [答案]A.
这样可排除图中其它线的干扰,便于确定两角的相对位置.易知①、②、③正确. [答案]A.
16.如图,OA⊥OB,OC⊥OD,垂足均为O.则∠BOC+∠AOD等于……( )
(A)150° (B)160° (C)170° (D)180°
 [提示]延长BO到E.
[提示]延长BO到E.
∵ OA⊥OB,
∴ OA⊥OE.
又 OC⊥O(D)
∴ ∠AOC+∠COE=∠AOC+∠AOD=90°.
由同角的余角相等知:∠COE=∠AOD.
∴ ∠BOC+∠AOD=∠BOC+∠COE=180°.
[答案]D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com