2．选用作业设计．

　　 作业设计

1．教材P₃₄ 习题22．1　 1、2．

　　 本节课要掌握：

　　 (1)一元二次方程的概念；(2)一元二次方程的一般形式ax²+bx+c=0(a≠0)和二次项、二次项系数，一次项、一次项系数，常数项的概念及其它们的运用．

　 　例3．求证：关于x的方程(m²-8m+17)x²+2mx+1=0，不论m取何值，该方程都是一元二次方程．

　　 分析：要证明不论m取何值，该方程都是一元二次方程，只要证明m²-8m+17≠0即可．

　　 证明：m²-8m+17=(m-4)²+1

　　 ∵(m-4)²≥0

　　 ∴(m-4)²+1>0，即(m-4)²+1≠0

　　 ∴不论m取何值，该方程都是一元二次方程．

　　 教材P₃₂　 练习1、2

　　 学生活动：请口答下面问题．

　　 (1)上面三个方程整理后含有几个未知数？

　　 (2)按照整式中的多项式的规定，它们最高次数是几次？

　　 (3)有等号吗？或与以前多项式一样只有式子？

　　 老师点评：(1)都只含一个未知数x；(2)它们的最高次数都是2次的；(3)都有等号，是方程．

　　 因此，像这样的方程两边都是整式，只含有一个未知数(一元)，并且未知数的最高次数是2(二次)的方程，叫做一元二次方程．

　　 一般地，任何一个关于x的一元二次方程，经过整理，都能化成如下形式ax²+bx+c=0(a≠0)．这种形式叫做一元二次方程的一般形式．

　　 一个一元二次方程经过整理化成ax²+bx+c=0(a≠0)后，其中ax²是二次项，a是二次项系数；bx是一次项，b是一次项系数；c是常数项．

　 　例1．将方程(8-2x)(5-2x)=18化成一元二次方程的一般形式，并写出其中的二次项系数、一次项系数及常数项．

　 　分析：一元二次方程的一般形式是ax²+bx+c=0(a≠0)．因此，方程(8-2x)(5-2x)=18必须运用整式运算进行整理，包括去括号、移项等．

　　 解：去括号，得：

　　 40-16x-10x+4x²=18

　　 移项，得：4x²-26x+22=0

　　 其中二次项系数为4，一次项系数为-26，常数项为22．

　 　例2．(学生活动：请二至三位同学上台演练)　 将方程(x+1)²+(x-2)(x+2)=1化成一元二次方程的一般形式，并写出其中的二次项、二次项系数；一次项、一次项系数；常数项．

　　 分析：通过完全平方公式和平方差公式把(x+1)²+(x-2)(x+2)=1化成ax²+bx+c=0(a≠0)的形式．

　　 解：去括号，得：

　 　x²+2x+1+x²-4=1

　　 移项，合并得：2x²+2x-4=0

　　 其中：二次项2x²，二次项系数2；一次项2x，一次项系数2；常数项-4．

　　 学生活动：列方程．

　　 问题(1)《九章算术》“勾股”章有一题：“今有户高多于广六尺八寸，两隅相去适一丈，问户高、广各几何？”

　　 大意是说：已知长方形门的高比宽多6尺8寸，门的对角线长1丈，那么门的高和宽各是多少？

　　 如果假设门的高为x尺，那么，这个门的宽为_______尺，根据题意，得________．

　　 整理、化简，得：__________．

问题(2)如图，如果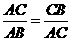，那么点C叫做线段AB的黄金分割点．

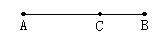
　　 如果假设AB=1，AC=x，那么BC=________，根据题意，得：________．

　　 整理得：_________．

　　 问题(3)有一面积为54m²的长方形，将它的一边剪短5m，另一边剪短2m，恰好变成一个正方形，那么这个正方形的边长是多少？

　　 如果假设剪后的正方形边长为x，那么原来长方形长是________，宽是_____，根据题意，得：_______．

　　 整理，得：________．

　　 老师点评并分析如何建立一元二次方程的数学模型，并整理．

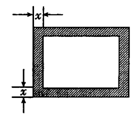
21．某大学为改善校园环境，计划在一块长80m，宽60m的长方形场地的中央建一个长方形网球场，网球场占地面积为3500m²．四周为宽度相等的人行走道，如图所示，若设人行走道的宽为xm．

　　 (1)你能列出相应的方程吗？

　　 (2)x可能小于0吗？说说你的理由．

　　 (3)x可能大于40吗？可能大于30吗？说说你的理由．

　　 (4)你知道人行走道的宽xm是多少吗？说说你的求解过程．

20．若方程(m-1)x²+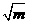x=1是关于x的一元二次方程，则m的取值范围是(　 )

　　 A．m≠1　　 B．m≥0　　 C．m≥0且m≠1　　 D．m为任意实数

19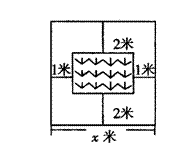．为争创市规范化学校，某中学向全体师生征集空地绿化　 方案，如图是李刚同学对其中一块正方形空地的设计图，中央绿地面积为24平方米，如果设正方形空地的边长为x，那么空地中央长方形绿地的长为______米，宽为______米，根据题意，可得方程___________．