5．当a_____时，关于x的方程5－a＝3 x+2的解为负数．

4．若|2a+1|＞2a+1，则a的取值范围是________．

2．若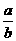＞1，则a，b应满足的条件是______． 3．若| x |＜1，则x的取值范围是_________．

1．在下列各题的横线上填入适当的不等号：

(1)若a－b＞0，则a______b；　　　　　 (2)若a－b＜0，则a______b；

(3)若a＞b，c______0时，ac＜bc；　　　 (4)若a＜b，c______0时，＜；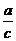

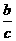(5)当a＞b，且a＞0，b＞0时，|a|_____|b|； (6)当a＜b，且a＜0，b＜0时，|a|_____|b|．

　 当x＝4时，代数式 A＝ax²－4x－6a的值是－1，那么当x＝－5 时，A的值是多少？

提示：关键在于利用一元一次方程求出a的值．

　　 据题意，有关于a的方程

16a－16－6a＝－1，

解得a＝1.5；

所以关于x的代数为

　　　　　 A＝1.5x²－4x－9，

于是，当x＝－5时，有

　 A＝1.5×(－5)²－4×(－5)－9

＝37.5+20－9 　　　　　　

　　　　 ＝48.5.

4．A、B两地相距49千米，某人步行从A地出发，分三段以不同的速度走完全程，共用10小时．已知第一段，第二段，第三段的速度分别是6千米/时，4千米/时，5千米/时，第三段路程为15千米，求第一段和第二段的路程．

答案：第一段路程长为18千米，第二段路程长为16千米．

提示：思路一：

三段路程之和为49千米，而路程等于时间与速度的乘积．

可设第一段路程长为 x千米，则第二段路程为(49－x－15)千米，

用时间的相等关系列方程，得

　　　 　　　　 ，

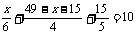解得　　　 x＝18(千米)；

由此可知，第一段路程长为18千米，第二段路程长为16千米．

思路二：

又可设走第一段所用时间为t小时，

由于第三段所用时间为 (小时)，

则第二段所用时间为(10－3－t)小时，

于是可用路程的相等关系列方程：

6t+(10－t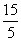－)×4+15＝49，

解得　 　　　 t＝3，

由此可知，第一段路程长为18千米，第二段路程长为16千米．

3．课外数学小组的女同学原来占全组人数的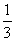，后来又有4个女同学加入，就占全组人数的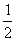，问课外数学小组原来有多少个同学．答案：12．

提示：计算女同学的总人数，她们占全体人数的一半．

设原来课外数学小组的人数为x，方程为

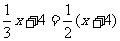
解得　　　 x＝12.

6.7x－．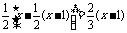

　略解：第一次去分母，得

　　　　　　　 42x－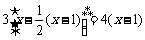

　　　 第一次去括号，得　 42x－，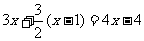　 　　　

　第二次去分母，得

　　　　　　　　 　　　78x+3x－3＝8x－8，

　　　 移项，合并同类项，得　 73x＝－5，

　　　 　把系数化为1，得

　　　　　　　　　　　　 　　x＝.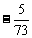

四 解关于x的方程(本题6分)：

b(a+x)－a＝(2b+1)x+ab (a≠0).

解：适当去括号，得

　　　　　　　　 ab+bx－a＝(2b+1)x+ab，

　　 移项，得

　　　　　　　 bx－(2b+1) x＝a+ab－ab，

　　 合并同类项，得

　　　　　　　　 (b－2b－1) x＝a，

即　　　－(b+1) x＝a，

当b≠－1时，有b+1 ≠0，方程的解为

　　　　　　　　　　　　 x＝．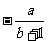

当b＝－1 时，有b+1＝0， 又因为 a≠0， 所以方程无解．(想一想，若a＝0，则如何？

五 列方程解应用题(每小题10分，共20分)：

5. x－；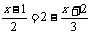　　　　　　　　　

　略解：去分母，得6x－3(x－1)＝12－2(x+2)

　　　 去括号，得　　　　 3x+3＝8－2x，　　　　　

移项，合并同类项，得　 5x＝5，　 　　　　　　　　　　　　　　　　　　

　　　 把系数化为1，得x＝1；　　　　　　　　　

3．2(0.3x+4)＝5+5(0.2x－7)；　　　　 　4. ；

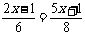　　 略解：去括号，得 0.6x+8＝5+ x－35，　　 略解：去分母，得 8x－4＝15 x+ 3，　　　　　　　　　　

　　　 移项，合并同类项，得－0.4x＝－38，　　　　　 　移项，合并同类项，得－7x＝7，

　　　 把系数化为1，得x＝95；　　　　　　　　　　 　把系数化为1，得　 x＝－1；