
题目列表(包括答案和解析)
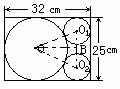
23.(改编)某乡薄铁社厂的王师傅要在长为25cm,宽为18cm的薄铁板上裁出一个最大的圆和两个尽可能大的小圆.他先画出了如图所示的草图,但他在求小圆半径时遇到了困难,请你帮助王师傅计算出这两个小圆的半径.
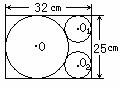
答案:连结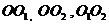 由题意得大圆的半径为9cm,设小圆的半径为r,在
由题意得大圆的半径为9cm,设小圆的半径为r,在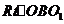 中可得
中可得 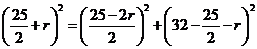 ,解得
,解得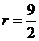 cm
cm
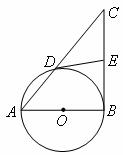
22.已知:如图,以△ABC的边 为直径的⊙O交边AC于点D,且过点D的切线DE平分边BC.
为直径的⊙O交边AC于点D,且过点D的切线DE平分边BC.
(1) 与⊙O是否相切?请说明理由;
与⊙O是否相切?请说明理由;
(2)当△ABC满足什么条件时,以点O,B,E,D为顶点的四边形是平行四边形?并说明理由.
答案:(1)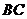 与⊙O相切.
与⊙O相切.
理由:连结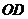 ,
,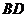 ,
,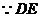 切⊙O于
切⊙O于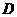 ,
, 为直径,
为直径,
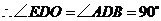 ,
,
又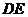 平分
平分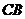 ,
,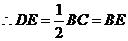 ,
,
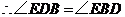 .又
.又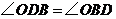 ,
,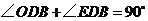 ;
;
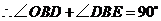 ,即
,即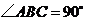 .
.
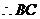 与⊙O相切.
与⊙O相切.
(2)当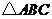 为等腰直角三角形
为等腰直角三角形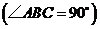 时,四边形
时,四边形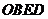 是平行四边形.
是平行四边形.
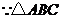 是等腰直角三角形
是等腰直角三角形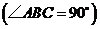 ,
,
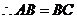 .
.
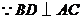 于
于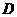 ,
,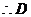 为
为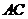 中点.
中点.
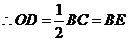 ,
, .
.
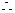 四边形
四边形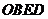 是平行四边形.
是平行四边形.
21.如图是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O,若∠OAB=25°,求∠A PB的度数.
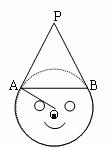
答案:解:∵PA、PB切⊙O于A、B,
∴PA=PB ,∴OA ⊥PA .
∵∠OAB=25°,∴∠PAB=65°
∴∠APB=180-65°×2=50°.

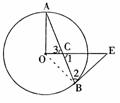
20.(2008黄冈市)已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
求证:DE是⊙O的切线.
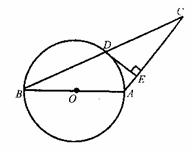
答案:解:BE与⊙O相切
理由:连接OB, ∵ 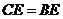
∴ 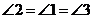 )
)
∵ 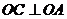 ,∴
,∴ 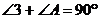 ,∴
,∴ 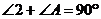
又∵ 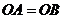 ,∴
,∴ 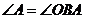 ,∴
,∴ 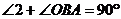
即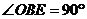 ,∴ BE与⊙O相切
,∴ BE与⊙O相切
19.(6分)(改编)如图8,已知 中,
中,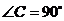 ,AC=3,BC=4,已点C为圆心作
,AC=3,BC=4,已点C为圆心作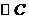 ,半径为
,半径为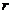 .
.
(1) 当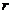 取什么值时,点AB与
取什么值时,点AB与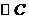 相切?
相切?
(2)当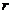 取什么值时,
取什么值时, 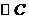 内与斜边
内与斜边 只有一个公共点?
只有一个公共点?

答案:解:(1)当圆与斜边 相切,如图 ∵
相切,如图 ∵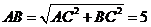 ∴
∴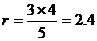
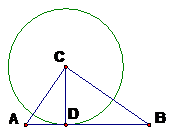
(2)由于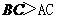 ,则以C为圆心,AC为半径的圆与AB交与A、B两点,如图,显然,当
,则以C为圆心,AC为半径的圆与AB交与A、B两点,如图,显然,当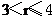 时,所作的圆与斜边AB只有一个公共点.
时,所作的圆与斜边AB只有一个公共点.
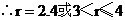
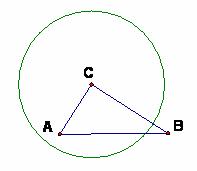
18.已知∠BAC=45°,一动点O在射线AB上运动(点O与点A不重合),设OA=x,如果半径为l的⊙O与射线AC只有一个公共点,那么x的取值范围是 .
答案: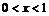 或
或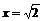
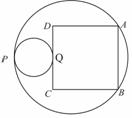
17. 如图,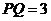 ,以
,以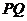 为直径的圆与一个以5为半径的圆相切于点P,正方形ABCD的顶点A、B在大圆上,小圆在正方形的外部且与CD切于点Q.则
为直径的圆与一个以5为半径的圆相切于点P,正方形ABCD的顶点A、B在大圆上,小圆在正方形的外部且与CD切于点Q.则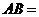 .
.
答案:6
16.在直角坐标系中,⊙O的圆心在圆点,半径为3,⊙A的圆心A的坐标为(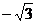 ,1),半径为1,那么⊙O与⊙A的位置关系是
.
,1),半径为1,那么⊙O与⊙A的位置关系是
.
答案:内切
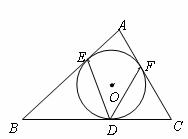
15.(原创)如图,⊙O内切于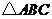 ,切点分别为
,切点分别为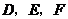 .已知
.已知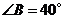 ,
,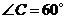 ,连结
,连结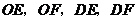 ,那么
,那么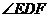 等于( )
等于( )
A.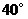 B.
B.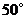 C.
C.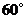 D.
D.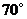
答案:B
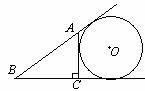
14.(改编)如图,AC⊥BC于点C,BC=8,CA=6,AB=10,⊙O与直线AB、 BC、CA都相切,则⊙O的半径等于 .
答案:4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com