
题目列表(包括答案和解析)
3. #已知两个等圆⊙O1和⊙O2相交于A、B两点,且⊙O1经过⊙O2,则四边形AO1BO2是( )
A.平行四边形 B.菱形 C.矩形 D.正方形
2. &若两圆没有公共点,则两圆的位置关系时间( )
A.只有外离 B. 外离或内含 C.相切 D.只有内含
答案:B
1.#两圆的半径为5 和3
和3 ,若圆心距为7
,若圆心距为7 ,则两圆的位置关系是(
)
,则两圆的位置关系是(
)
A.外离 B.外切 C.相交 D.内切
答案:C
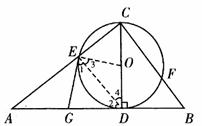
26.答案:(1)在△ABC中,∵AB=AC,
∴∠ABC=∠C.
∵DE∥BC,∴∠ABC=∠E,
∴∠E=∠C.
又∵∠ADB=∠C,
∴∠ADB=∠E.
(2)当点D是弧BC的中点时,DE是⊙O的切线.
理由是:当点D是弧BC的中点时,则有AD⊥BC,且AD过圆心O.
 又∵DE∥BC,∴ AD⊥ED.
又∵DE∥BC,∴ AD⊥ED.
∴ DE是⊙O的切线.
(3)连结BO、AO,并延长AO交BC于点F,
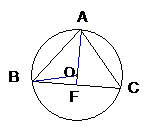 则AF⊥BC,且BF=
则AF⊥BC,且BF=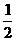 BC=3.
BC=3.
又∵AB=5,∴AF=4.
设⊙O的半径为 ,在Rt△OBF中,OF=4-
,在Rt△OBF中,OF=4- ,OB=
,OB= ,BF=3,
,BF=3,
∴ 
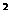 =3
=3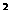 +(4-
+(4- )
)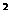
解得 =
=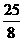 ,
∴⊙O的半径是
,
∴⊙O的半径是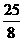 .
.
25.解:连接OE、DE.
∵CD 是 的直径,
的直径,
∴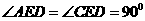
∵G是AD的中点
∴
故GE是 的切线.
的切线.
答案:解:(1)所画⊙P如图所示,由图可知⊙P的半径为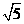 ,而
,而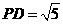 .
.
 点
点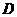 在⊙P上.
在⊙P上.
(2)① 直线
直线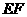 向上平移1个单位经过点
向上平移1个单位经过点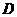 ,
,
且经过点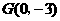 ,
,
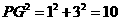 ,
,
 ,
,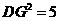 .
.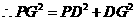 .
.
则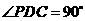 ,
,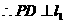 .
. 直线
直线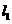 与⊙P相切.
与⊙P相切.
②
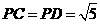 ,
,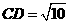 ,
,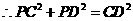 .
.
 .
.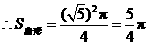 ,
,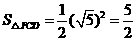 .
.
24.证明:过点Ol、O2分别作OlC⊥MN、O2D⊥MN,垂足为C、D,
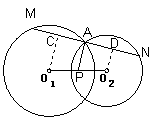 则OlC∥PA∥O2D,且AC=
则OlC∥PA∥O2D,且AC= 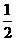 AM,AD=
AM,AD= 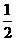 AN.
AN.
∵OlP= O2P ,
∴AD=AM,∴AM=AN.
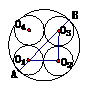
23.截法如图,根据圆的对称性可知,O1,O3都在⊙O的直径AB上,设所截出的凳面直径为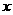 ,则
,则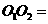 x,
x,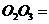 x,
x, 
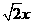 ,又
,又 AB-(O1A+O3B)=50-x,所以
AB-(O1A+O3B)=50-x,所以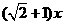 =50,所以x=50(
=50,所以x=50(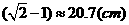
22.(1)图略 (2)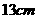
21.(1)提示:作∠AOB的角平分线,延长成为直线即可;
 (2)∵扇形的弧长为
(2)∵扇形的弧长为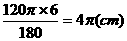 ,∴底面的半径为
,∴底面的半径为 ,
,
∴圆锥的底面积为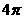
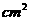 。
。
20.AB=24cm. 连接OC,OA.∵AB与内圆相切与点C, ∴OC⊥AB. ∴AC=BC=12cm.∴横截面积为:πAO2-πOC2=π(AO2-OC2.∵在Rt△ACO中,AO2-OC2=AC2 ,∴横截面积=πAC2 (6分)=144π(cm2) .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com