11-20　 CACAC　 DAABC

提示：18、∵△ABC为等边三角形　 ∴∠B=∠C=60°，又∠APD=60°

∴∠BAP+∠APB=∠APB+∠CPD=120°，∴∠BAP=∠DPC，∴△APB∽△PCD

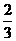∴：1=(AB-1)：AB　 ∴AB=3

20、∵AE²+EF²=4²+3²=5²=AF²

∴∠AEF=90°，∴易证△ABE∽△EFC　 ∴AB：EC=4：3 设AB=x

x：(x-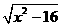)=4：3　 ∴x²=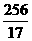

10、如题图：EF=DE=8-3=5　 ∵EC=3，∴FC=4，易证△ABF∽△EFC

∴BF：3=8：4　 BF=6

∴S_阴影=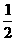·6·8+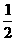·4·3=30

9、∵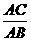==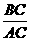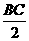，又∵=

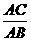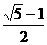
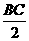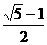∴=　 ∴BC=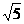-1　 ∴AB=2+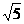-1=1+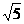

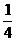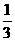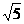1-10　 8　 　2　 4　 7：4　 30　 5，20　 　1+　 30　

提示：4、如图1，过D分别作BC、AB的平分线有两条，另外，作∠ADE=∠ABC又一条，作∠CDF=∠ABC又一条，共4条

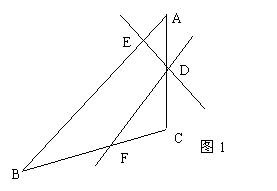
8、====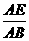

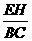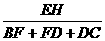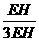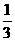
27、(8分)若矩形的一个短边与长边的比值为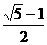，(黄金分割数)，我们把这样的矩形叫做黄金矩形

(1)　　　 操作：请你在如图15所示的黄金矩形ABCD(AB＞AD)中，以短边AD为一边作正方形AEFD。

(2)　　　 探究：在(1)中的四边形EBCF是不是黄金矩形？若是，请予以证明；若不是，请说明理由。

(3)　　　 归纳：通过上述操作及探究，请概括出具体有一般性的结论(不需证明)

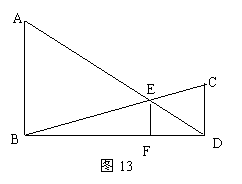
26、(7分)已知，如图13，AB⊥BD，CD⊥BD，垂足分别为B、D，AD和BC交于点E，EF⊥BD，垂足为F，我们可以证明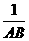+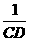=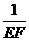成立，若将图13中的垂直改为斜交，如图14，AB∥CD，AB与BC交于点E，过点E作EF∥AB交BD于F，则

(1)　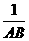　　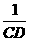 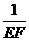+=还成立吗？如果成立，给出证明；如果不成立，请说明理由。

(2)　　　 请找出S_△ABC，S_△BED和S_△BDC间的关系，并给出证明。

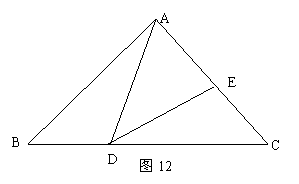
25、如图12，△ABC中，∠BAC=90°，AB=AC=1，点D是BC上一个动点(不与B、C重合)，在AC上取E点，使∠ADE=45°

(1)　　　 求证：△ABD∽△DCE

(2)　　　 设BD=x，AE=y，求y与x的函数关系式

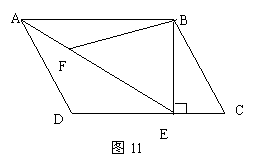
24、如11图，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，连结AE，F为AE上一点，且∠BFE=∠C

(1)　　　 求证：△ABF∽△EAD

(2)　　　 若AB=4，S_ABCD=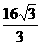，求AE的长

(3)　　　 在(1)、(2)条件下，若AD=3，求BF的长(计算结果可含根号)

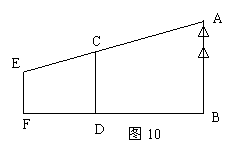
23、如图10，为了测量一棵树AB的高度，测量者在D点立一高CD等于2m的标杆，现测量者从E处可以看到标杆顶点C与树顶A在同一条直线上，如果测得BD=20m，FD=4m，EF=1.8m，求树高。

22、已知四边形ABCD与四边形A′B′C′D′相似，且AB：BC：CD：DA=20：15：9：8，四边形A′B′C′D′的周长为26，求四边形A′B′C′D′各边的长。