
题目列表(包括答案和解析)
1、(02年湖北黄冈)已知:如图1,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明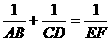 成立(不要求考生证明).
成立(不要求考生证明).
若将图1中的垂线改为斜交,如图2,AB∥CD,AD,BC相交于点E,
过点E作EF∥AB,交BD于点F,则:
(1)

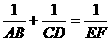 还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
(2) 请找出S△ABD,S△BED和S△BDC间的关系式,并给出证明.
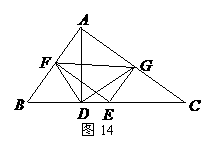
22.(10分)如图14,在 中,
中,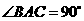 ,
,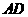 是
是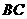 边上的高,
边上的高,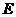 是
是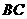 边上的一个动点(不与
边上的一个动点(不与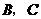 重合),
重合),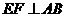 ,
,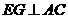 ,垂足分别为
,垂足分别为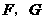 .
.
(1)求证: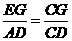 ;
;
(2)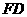 与
与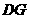 是否垂直?若垂直,请给出证明;若不垂直,请说明理由;
是否垂直?若垂直,请给出证明;若不垂直,请说明理由;
(3)当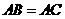 时,
时,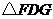 为等腰直角三角形吗?并说明理由.
为等腰直角三角形吗?并说明理由.
21.(10分)如图13,在正方形ABCD中,P是CD上一动点(与C、D不重合),使三角板的直角顶点与P重合,并且一条直角边经过点B,另一条直角边所在的直线交于点E.
探究:(1)观察操作作结果,你发现哪个三角形与△BPC相似?为什么?
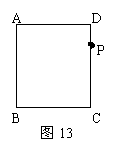 (2)当P点位于CD的中点时,(1)中两个相似三角形周长的比是多少?
(2)当P点位于CD的中点时,(1)中两个相似三角形周长的比是多少?
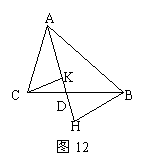
20.(8分)如图12,AD是∠BAC的角平分线,交△ABC的边BC于点D,BH⊥AD,CK⊥AD,垂足分别为H、K,你能说明AB·DK=AC·DH吗?
19.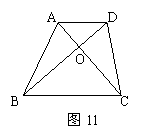 (8分)如图10,梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,问:△AOB与△COD是否相似?
(8分)如图10,梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,问:△AOB与△COD是否相似?
有一名同学解答如下:
因为AD∥BC,所以∠ADO=∠CBO,∠DAO=∠BCO,
所以△AOD∽△BOC,所以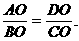 又因为∠AOB=∠DOC,所以△AOB∽△COD.
又因为∠AOB=∠DOC,所以△AOB∽△COD.
请判断这名同学的证明是否正确,说明理由.
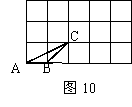
18.(8分)如图10,在一个3×5的正方形网格中,△ABC的顶点A,B,C在单位正方形顶点上,请你在图中画一个△A1,B1,C1都在单位正方形的顶点上.

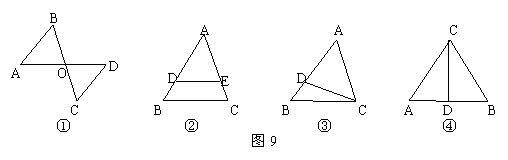
17.(8分)图9是几组三角形的组合图形,图①中,△AOB∽△DOC;图②中,△ABC∽△ADE;图③中,△ABC∽△ACD;图④中,△ACD∽△CBD.
小Q说:图①、②是位似变换,其位似中心分别是O和A.
小R说:图③、④是位似变换,其位似中心是点D.
请你观察一番,评判小Q,小R谁对谁错.
16.我们可以用下面的方法测出月球的距离:如图9,在月圆时,把一个五分的硬币(直径约为2.4cm),放在离眼O约2.6m的AB处,正好把月亮遮住,已知月球的直径约为3500km,那么月球与地球的距离约为_________.
15.如图8,△EDC是由△ABC缩小得到的,A(-3,5),那么点E的坐标是________.
14.如图7,△ABC中,AB>AC,过AC上一点D作直线DE,交AB于E,使△ADE与△ABC相似,这样的直线可作_______条.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com