
题目列表(包括答案和解析)
6.已知:如图,∠ADE=∠ACD=∠ABC,图中相似三角形共有………………( )
(A)1对 (B)2对 (C)3对 (D)4对

 (7)
(7) (8)
(8)
5.如图,在Rt△ABC中,CD是斜边AB上的高,则图中的相似三角形共有……( )
(A)1对 (B)2对 (C)3对 (D)4对
4.下列判断中,正确的是………………………………………………………( )
(A)各有一个角是67°的两个等腰三角形相似
(B)邻边之比都为2︰1的两个等腰三角形相似
(C)各有一个角是45°的两个等腰三角形相似
(D)邻边之比都为2︰3的两个等腰三角形相似
3.如图,DE∥BC,在下列比例式中,不能成立的是………………………………( )

 (第5题)
(第5题)
(A)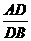 =
= (B)
(B)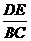 =
= (C)
(C) =
= (D)
(D)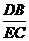 =
=
2.已知线段d是线段a、b、c的第四比例项,其中a=2 cm,b=4 cm,c=5 cm,则d等于……( )
(A)1
cm(B)10
cm(C) cm(D)
cm(D)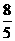 cm.
cm.
1.已知5y-4x=0,那么(x+y)︰(x-y)的值等于……………………………( )
(A)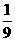 (B)-9 (C)9 (D)-
(B)-9 (C)9 (D)-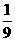
30.如图,在Rt△ABC中,∠C=90°,BC=6 cm,CA=8 cm,动点P从点C出
发,以每秒2 cm的速度沿CA、AB运动到点B,则从C点出发多少秒时,可使
S△BCP= S△ABC?
S△ABC?

[提示]先求CP,再求DP.
[答案]当点P从点C出发,运动在CA上时,若S△BCP= S△ABC,则
S△ABC,则
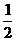 ·CP·BC=
·CP·BC= ·
·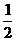 AC·BC,
AC·BC,
∴ CP= ·AC=2(cm).
·AC=2(cm).
故由点P的运动速度为每秒2 cm,它从C点出发1秒时,有S△BCP= S△ABC.当点P从点C出发运动到AB上时,如图,可过点P作PD⊥BC于D.
S△ABC.当点P从点C出发运动到AB上时,如图,可过点P作PD⊥BC于D.
若S△BCP= S△ABC,则
S△ABC,则

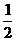 PD·BC=
PD·BC= ·
·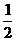 AC·BC.
AC·BC.
∴ PD= AC=2(cm).
AC=2(cm).
∵ Rt△BAC∽Rt△BPD,
∴  =
=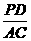 .
.
又 AB=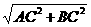 =10,
=10,
故 BP=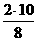 =
= ,AP=AB-BP=10-
,AP=AB-BP=10- =7.5.
=7.5.
也就是说,点P从C出发共行15.5 cm,用去7.75秒,此时S△BCP= S△ABC.
S△ABC.
答:1秒或7.75秒.
29.如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连结FC
(AB>AE).
(1)△AEF与△EFC是否相似?若相似,证明你的结论;若不相似,请说明理由;
(2)设 =k,是否存在这样的k值,使得△AEF∽△BFC,若存在,证明你的结论并求出k的值;若不存在,说明理由.
=k,是否存在这样的k值,使得△AEF∽△BFC,若存在,证明你的结论并求出k的值;若不存在,说明理由.

[提示](1)如图,证明△AFE≌△DGE,证出∠AFE=∠EFC.
(2)证明∠ECG=30°,∠BCF=30°.
[答案]如图,是相似.

[证明]延长FE,与CD的延长线交于点G.
在Rt△AEF与Rt△DEG中,
∵ E是AD的中点,∴ AE=ED.
∵ ∠AEF=∠DEG,∴ △AFE≌△DGE.
∴ ∠AFE=∠DGE.∴ E为FG的中点.
又 CE⊥FG,∴ FC=GC.∴ ∠CFE=∠G.∴ ∠AFE=∠EFC.
又 △AEF与△EFC均为直角三角形,∴ △AEF∽△EFC.
① 存在.如果∠BCF=∠AEF,即k= =
= 时,△AEF∽△BCF.
时,△AEF∽△BCF.
证明:当 =
= 时,
时, =
=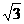 ,∴ ∠ECG=30°.
,∴ ∠ECG=30°.
∴ ∠ECG=∠ECF=∠AEF=30°.∴ ∠BCF=90°-60°=30°.
又 △AEF和△BCF均为直角三角形,∴ △AEF∽△BCF.
② 因为EF不平行于BC,∴ ∠BCF≠∠AFE.∴ 不存在第二种相似情况.
28.如图,∠ABC=∠CDB=90°,AC=a,BC=b.
(1)当BD与a、b之间满足怎样的关系时,△ABC∽△CDB?
(2)过A作BD的垂线,与DB的延长线交于点E,若△ABC∽△CDB.
求证四边形AEDC为矩形(自己完成图形).

[提示]利用三角形相似,推出BD= .
.
[答案](1)∵ ∠ABC=∠CDB=90°,∴ 当 =
= 时,△ABC∽△CDB.
时,△ABC∽△CDB.
即  =
= .∴ BD=
.∴ BD= .即当BD=
.即当BD= 时,△ABC∽△CDB.
时,△ABC∽△CDB.
∵ △ABC∽△CDB,∴ ∠ACB=∠CBD.∴ AC∥ED.
又 ∠D=90°,∴ ∠ACD=90°.∴ ∠E=90°.∴ 四边形AEDC为矩形.
27.如图,BD、CE分别是△ABC的两边上的高,过D作DG⊥BC于G,分别交CE及BA的延长线于F、H,求证:
(1)DG2=BG·CG;(2)BG·CG=GF·GH.
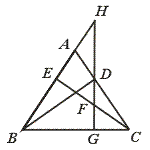
[提示](1)证△BCG∽△DCG;(2)证Rt△HBG∽Rt△CFG.
[答案](1)DG为Rt△BCD斜边上的高,
∴ Rt△BDG∽Rt△DCG.∴ 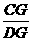 =
=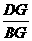 ,即DG2=BG·CG.
,即DG2=BG·CG.
(2)∵ DG⊥BC, ∴ ∠ABC+∠H=90°,CE⊥AB.
∴ ∠ABC+∠ECB=90°.∴ ∠ABC+∠H=∠ABC+∠ECB.∴ ∠H=∠ECB.
又 ∠HGB=∠FGC=90°,∴ Rt△HBG∽Rt△CFG.∴  =
= ,
,
∴ BG·GC=GF·GH.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com