
题目列表(包括答案和解析)
2.气象台预报“本市明天降水概率是80%”.对此信息,下列说法正确的是( D )
A.本市明天将有80%的地区降水 B.本市明天将有80%的时间降水
C.明天肯定下雨 D.明天降水的可能性比较大
1.下列事件是必然发生事件的是( C )
A.打开电视机,正在转播足球比赛
B.小麦的亩产量一定为1000公斤
C.在只装有5个红球的袋中摸出1球,是红球
D.农历十五的晚上一定能看到圆月
23.(1)证明: 如图1,连接OD.
∵ OA=OD, AD平分∠BAC,
∴ ∠ODA=∠OAD, ∠OAD=∠CAD。
∴ ∠ODA=∠CAD。
∴ OD//AC。
∴ ∠ODB=∠C=90°。
 ∴
BC是⊙O的切线。
图1
∴
BC是⊙O的切线。
图1
(2)解法一: 如图2,过D作DE⊥AB于E.
∴ ∠AED=∠C=90°.
又∵ AD=AD, ∠EAD=∠CAD,
∴ △AED≌△ACD.
∴ AE=AC, DE=DC=3。
在Rt△BED中,∠BED =90°,由勾股定理,得 图2
BE=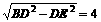 。
。
设AC=x(x>0), 则AE=x。
在Rt△ABC中,∠C=90°, BC=BD+DC=8, AB=x+4, 由勾股定理,得
x2 +82= (x+4) 2。
解得x=6。
即 AC=6。
解法二: 如图3,延长AC到E,使得AE=AB。
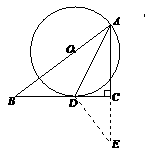 ∵
AD=AD, ∠EAD =∠BAD,
∵
AD=AD, ∠EAD =∠BAD,
∴ △AED≌△ABD.
∴ ED=BD=5。
在Rt△DCE中,∠DCE=90°, 由勾股定理,得
CE=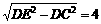 。
。
在Rt△ABC中,∠ACB=90°, BC=BD+DC=8, 由勾股定理,得
AC2 +BC2= AB 2。 图3
即 AC2 +82=(AC+4) 2。
解得 AC=6。
23.如图,在△ABC中,∠C=90°, AD是∠BAC的平分线,O是AB上一点, 以OA为半径的
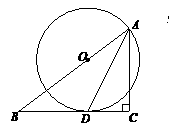 ⊙O经过点D。
⊙O经过点D。
(1)求证: BC是⊙O切线;
(2)若BD=5, DC=3, 求AC的长。

22. 解:⑴设每件衬衫应降价x元。
根据题意,得 (40-x)(20+2x)=1200
整理,得x2-30x+200=0
解之得 x1=10,x2=20。
因题意要尽快减少库存,所以x取20。
答:每件衬衫应降价20元。
⑵商场每天盈利(40-x)(20+2x)=800+60x-2x2=-2(x-15)2+1250.
当x=15时,商场最大盈利1250元。
答:每件衬衫降价15元时,商场平均每天盈利最多。
22.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元。为了扩大销售,
增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬
衫每降价1元,商场平均每天可多售出2件。
⑴ 若商场平均每天要盈利1200元,每件衬衫应降价多少元?
⑵每件衬衫降价多少元,商场平均每天盈利最多?
21.解:(1)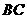 所在直线与小圆相切,
所在直线与小圆相切,
理由如下:过圆心 作
作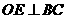 ,垂足为
,垂足为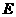 ,
,
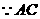 是小圆的切线,
是小圆的切线,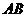 经过圆心
经过圆心 ,
,
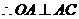 ,又
,又
 平分
平分 。
。
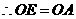 .
.
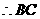 所在直线是小圆的切线。
所在直线是小圆的切线。
(2)
理由如下:连接 。
。
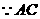 切小圆
切小圆 于点
于点 ,
,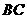 切小圆
切小圆 于点
于点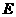 ,
,
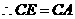 .
.
 在
在 与
与 中,
中,
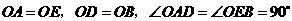 ,
,
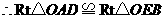 (HL)
(HL) 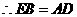 。
。
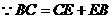 ,
,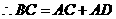 .
.
(3) ,
,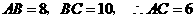 .
.
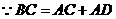 ,
,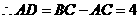 。
。
 圆环的面积
圆环的面积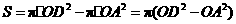
又 ,
, 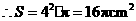 。
。
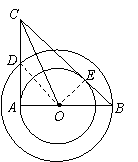
21.如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A、与大圆相
交于点B。小圆的切线AC与大圆相交于点D,且CO平分∠ACB。
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由;
(3)若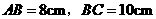 ,求大圆与小圆围成的圆环的面积。(结果保留π)
,求大圆与小圆围成的圆环的面积。(结果保留π)
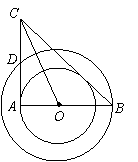
20.AD=2,BE=3,CF=4。
20.如图,⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F、若AB=5,AC=6,
BC=7,求AD、BE、CF的长。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com