22．解法1：用表格说明

解法2：用树状图来说明

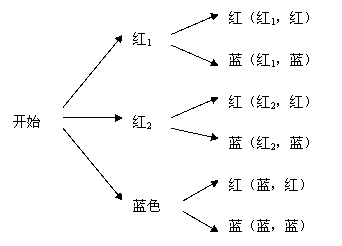
所以配成紫色得概率为P(配成紫色)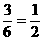＝，所以游戏者获胜得概率为。

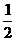22．小颖为九年级1班毕业联欢会设计了一个“配紫色”的游戏：如图是两个可以自由转动

的转盘，每个转盘被分成面积相等的几个扇形，游戏者同时转动两个转盘，两个转盘停

止转动时，若有一个转盘的指针指向蓝色，另一个转盘的指针指向红色，则“配紫色”

成功，游戏者获胜，求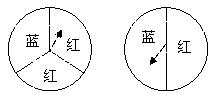游戏者获胜的概率。

21．解：(用列表法来解)

(1)所有可能结果为：

由表格可知，小夏获胜的可能为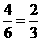：；小秋获胜的可能性为：。

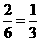(2)同上表，易知，和的可能性中，有三个奇数、三个偶数；三个质数、三个合数。

因此，游戏规则可设计为：如果和为奇数，小夏胜；为偶数，小秋胜。(答案不唯一)

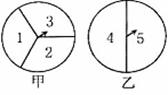
21．如图，甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形．小夏和

小秋利用它们来做决定获胜与否的游戏．规定小夏转甲盘一次、小秋转乙盘一次为一次

游戏(当指针指在边界线上时视为无效，重转)。

(1)小夏说：“如果两个指针所指区域内的数之和为6或7，则我获胜；否则你获胜”。

按小夏设计的规则，请你写出两人获胜的可能性分别是多少?

(2)请你对小夏和小秋玩的这种游戏设计一种公平的游戏规则，并用一种合适的方法

(例如：树状图，列表)说明其公平性。

20．分析：(1)和(2)可用实验获得频率的稳定值去估计概率；(3)可用白球(或黑球)

的概率去估计在总体中所占比值；(4)是统计思想和概率知识的综合应用。

(1)观察表格得摸到白球的频率将会接近0.6；

(2)摸到白球的概率是0.6；摸到黑球的概率是1-0.6=0.4；

(3)∵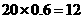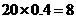；　 　∴黑球8个，白球12个；

(4)①先从不透明的口袋里摸出a个白球，都涂上颜色(如黑色)，然后放回口袋里，

搅拌均匀；②将搅匀后的球从中随机摸出一个球记下颜色,再把它放回袋中,不断大

量重复n，记录摸出黑球频数为b；③根据用频数估计概率的方法可得出白球数为

。

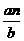说明：本题考查用实验获得频率去估计概率方法和用样本估计总体的统计思想。

20．在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只，某学习小组

做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复.

表是活动进行中的一组统计数据：

摸球的次数	100	150	200	500	800	1000
摸到白球的次数	58	96	116	295	484	601
摸到白球的频率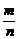	0.58	0.64	0.58	0.59	0.605	0.601

⑴ 请估计：当很大时，摸到白球的频率将会接近　　　　　 ；

⑵ 假如你去摸一次，你摸到白球的概率是　　　　 ，摸到黑球的概率是　　　　 ；

⑶ 试估算口袋中黑、白两种颜色的球各有多少只?

⑷ 解决了上面的问题，小明同学猛然顿悟，过去一个悬而未决的问题有办法了.这个问

题是:在一个不透明的口袋里装有若干个白球,在不允许将球倒出来数的情况下,如

何估计白球的个数(可以借助其他工具及用品)？请你应用统计与概率的思想和方法

解决这个问题，写出解决这个问题的主要步骤及估算方法。

6、7、8、9、10；6、7、8、9、10、11；7、8、9、10、11、12。

∵抛两枚骰子两个朝上面点数和有36种情况，出现两个朝上面点数和为7有6次情况。

∴出现两个朝上面点数和为7的概率为。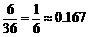

而试验20000次出现两个朝上面点数和为7的频率为。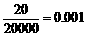

因为多数次试验的频率应接近概率，而0.001和0.167相差很大，所以两枚骰子质量不都合格。

说明：大量重复实验时事件发生频率将趋近于稳定，且稳定在概率的附近。

2、3、4、5、6、7；3、4、5、6、7、8；4、5、6、7、8、9；5、

19．分析：本题可通过分别计算出现两个朝上面点数和为7的概率和实验20000次出现两个

朝上面点数和为7的频率，然后依据大量重复实验时事件发生频率与事件发生概率的差

距将很小，来确定质量是否都合格。

解：两枚骰子质量不都合格．同时抛两枚骰子两个朝上面点数和有以下情况：

19．小明为了检验两枚六个面分别刻有点数1、2、3、4、5、6的正六面体骰子的质量是否

都合格，在相同的条件下，同时抛两枚骰子20000次，结果发现两个朝上面的点数和是

7的次数为20次．你认为这两枚骰子质量是否都合格(合格标准为：在相同条件下抛骰

子时，骰子各个面朝上的机会相等)？并说明理由。