
题目列表(包括答案和解析)
1.下面的图形中,既是轴对称图形又是中心对称图形的是( B )


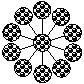

A. B. C. D.
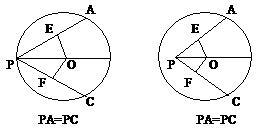
23.(1)证明:过O作OE⊥PB于E,OF⊥PD于F。
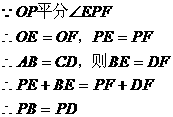
(2)上述结论仍成立。如下图所示。证明略。
23.如图所示,已知O是∠EPF的平分线上的一点,以O为圆心的圆与角的两边分别交于点A、B和C、D。
⑴求证:PB=PD。
⑵若角的顶点P在圆上或圆内,⑴中的结论还成立吗?若不成立,请说明理由;若成立,请加以证明。
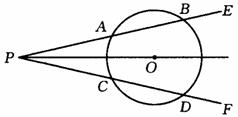
22.证明:(1)∵AB为⊙O的直径,CD是弦,且AB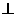 CD于E,
CD于E,
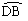
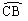 ∴CE=ED, =
∴CE=ED, =
∴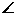 BCD=
BCD=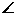 BAC
BAC
∵OA=OC ∴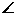 OAC=
OAC=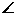 OCA
OCA
∴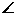 ACO=
ACO=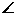 BCD
BCD
(2)设⊙O的半径为Rcm,则OE=OB EB=R
EB=R 8,
8,
CE=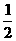 CD=
CD=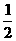
 24=12
24=12
在Rt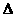 CEO中,由勾股定理可得
CEO中,由勾股定理可得
OC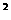 =OE
=OE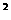 +CE
+CE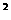 即R
即R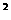 = (R
= (R 8)
8)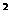 +12
+12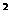
解得 R=13 。 ∴2R=2 13=26 。
13=26 。
答:⊙O的直径为26cm。
22.如图所示,已知AB为⊙O的直径,CD是弦,且AB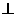 CD于点E。连接AC、OC、BC。
CD于点E。连接AC、OC、BC。
 (1)求证:
(1)求证: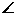 ACO=
ACO=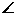 BCD。
BCD。
(2)若EB= ,CD=
,CD= ,求⊙O的直径。
,求⊙O的直径。
21.如图所示,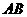 是⊙O的一条弦,
是⊙O的一条弦,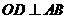 ,垂足为
,垂足为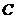 ,交⊙O于点D,点
,交⊙O于点D,点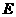 在⊙O
在⊙O
上。
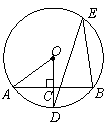 (1)若
(1)若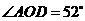 ,求
,求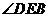 的度数;
的度数;



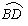 (2)若
(2)若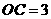 ,
,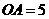 ,求
,求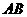 的长。
的长。
|
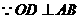 , = 。
, = 。
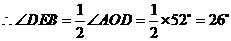
(2)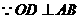 ,
,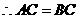 ,
, 为直角三角形,
为直角三角形,
 ,
,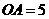 ,
,
由勾股定理可得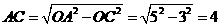
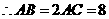 。
。
20.AE=BE。提示:连结AC或补成完整的圆延长AD应用垂径定理。
20. 
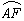
 如图,BC为⊙O的直径,AD⊥BC,垂足为D。 = ,BF和AD相交于E。试猜
如图,BC为⊙O的直径,AD⊥BC,垂足为D。 = ,BF和AD相交于E。试猜
 想AE与BE的长度之间的关系,并请说明理由。
想AE与BE的长度之间的关系,并请说明理由。
19.连接OQ,
∵RQ为⊙O的切线,∴∠OQR=90°。
∴∠PQR+∠BQO=90°。
又∵OA⊥OB, ∴∠B+∠BPO=90°。
∵OB=OQ,∴∠B=∠BQO . ∴∠BPO=∠PQR.。
∴RP=RQ。
19.如图,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点,BP的延长线交⊙O于Q,
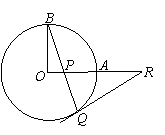 过Q的⊙O的切线交OA的延长线于R。求证:
RP=RQ。
过Q的⊙O的切线交OA的延长线于R。求证:
RP=RQ。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com