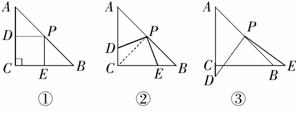
23．操作：在△ABC中，AC＝BC＝2，∠C＝90°，将一块等腰三角板的直角顶点放在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于D、E两点．如图①、②、③是旋转三角板得到的图形中的3种情况，研究：

　(1)三角板绕点P旋转，观察线段PD与PE之间有什么数量关系？并结合图②说明理由．

　(2)三角板绕点P旋转，△PBE是否能成为等腰三角形？若能，指出所有情况(即写出△PBE为等腰三角形时CE的长)；若不能，请说明理由．

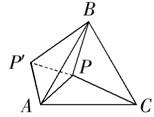
22．解：连接PP′，由题意可知BP′=PC＝10，AP′=AP，

∠PAC＝P^/AB，而∠PAC+∠BAP＝60°，

所以∠PAP′＝60°。故△APP′为等边三角形，

所以PP′＝AP＝AP′＝6；又利用勾股定理的逆定理可知：

PP^/2+BP²＝BP^/2，所以△BPP′为直角三角形，且∠BPP′＝90°，

可求∠APB＝90°+60°＝150°。　　　　

22．如图，P是正三角形ABC 内的一点，且PA＝6，PB＝8，PC＝10。若将△PAC绕点A逆时针旋转后，得到△P^/AB。

⑴求点P与点P′之间的距离；⑵∠APB的度数。

21．解：建立如图所示的直角坐标系，则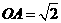，所以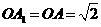，所以点A₁的坐标是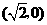．因为∠AOB＝45°，所以△AOB是等腰直角三角形。所以△A₁OB₁是等腰直角三角形，且OA₁边上的高为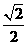，所以点B_l的坐标是。

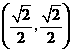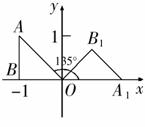
21．已知平面直角坐标系上的三个点O(0，0)，A(－1，1)，B(－1，0)，将△ABO绕点O

按顺时针方向旋转135°，点A、B的对应点为A_l ，B_l，求点A_l ，B_l的坐标。

20．(1)图略．(2)图略，A₁点坐标为(－1，1)。

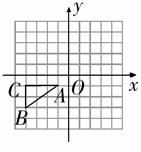
20．如图，已知△ABC的顶点A、B、C的坐标分别是A(－1，－1)， B(－4，－3)，

C(－4，－1)。

　(1)作出△ABC关于原点O的中心对称图形；

　(2)将△ABC绕原点O按顺时针方向旋转90°后得到△A₁B₁C₁，画出△A₁B₁C₁，并写出

点A₁的坐标。

19．(1)如图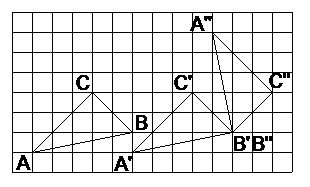

(2)能，将△ABC绕CB、C^//B^//延长线的交点顺时针旋转90度。

19．如图，把△ABC向右平移5个方格，再绕点B顺时针方向旋转90°。

(1)画出平移和旋转后的图形，并标明对应字母；

(2)能否把两次变换合成一种变换，如果能，说出变换过程(可适当在图形中标记)；如

果不能，说明理由。

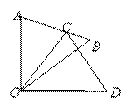
18．解：∵CO=AO，∠AOC＝40°，∠BOD＝40°，

∴∠OAC＝70°，∠AOB＝50°，∴∠B＝60°。