
题目列表(包括答案和解析)
8. (2009年宜宾)已知:如图,在平面直角坐标系 O
O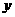 中,Rt△OCD的一边OC在
中,Rt△OCD的一边OC在 轴上,∠C=90°,点D在第一象限,OC=3,DC=4,反比例函数的图象经过OD的中点A.
轴上,∠C=90°,点D在第一象限,OC=3,DC=4,反比例函数的图象经过OD的中点A.
(1)求该反比例函数的解析式;
(2)若该反比例函数的图象与Rt△OCD的另一边DC交于点B,求过A、B两点的直线的解析式.

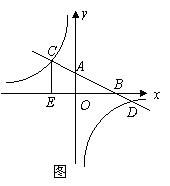
7.(2009年重庆)已知:如图,在平面直角坐标系 中,直线AB分别与
中,直线AB分别与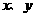 轴交于点B、A,与反比例函数的图象分别交于点C、D,
轴交于点B、A,与反比例函数的图象分别交于点C、D,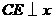 轴于点E,
轴于点E,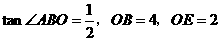 .
.
(1)求该反比例函数的解析式;
(2)求直线AB的解析式.

6.(2009年舟山)水产公司有一种海产品共2 104千克,为寻求合适的销售价格,进行了8天试销,试销情况如下:
|
|
第1天 |
第2天 |
第3天 |
第4天 |
第5天 |
第6天 |
第7天 |
第8天 |
|
售价x(元/千克) |
400 |
|
250 |
240 |
200 |
150 |
125 |
120 |
|
销售量y(千克) |
30 |
40 |
48 |
|
60 |
80 |
96 |
100 |
观察表中数据,发现可以用反比例函数刻画这种海产品的每天销售量y(千克)与销售价格x(元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量y(千克)与销售价格x(元/千克)之间都满足这一关系.
(1) 写出这个反比例函数的解析式,并补全表格;
(2) 在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出?
(3) 在按(2)中定价继续销售15天后,公司发现剩余的这些海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务?
5.(2009年衢州)水产公司有一种海产品共2 104千克,为寻求合适的销售价格,进行了8天试销,试销情况如下:
|
|
第1天 |
第2天 |
第3天 |
第4天 |
第5天 |
第6天 |
第7天 |
第8天 |
|
售价x(元/千克) |
400 |
|
250 |
240 |
200 |
150 |
125 |
120 |
|
销售量y(千克) |
30 |
40 |
48 |
|
60 |
80 |
96 |
100 |
观察表中数据,发现可以用反比例函数刻画这种海产品的每天销售量y(千克)与销售价格x(元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量y(千克)与销售价格x(元/千克)之间都满足这一关系.
(1) 写出这个反比例函数的解析式,并补全表格;
(2) 在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出?
4.(2009年湘西自治州)21.在反比例函数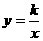 的图像的每一条曲线上,
的图像的每一条曲线上,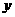 都随
都随 的增大而减小.
的增大而减小.
(1) 求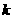 的取值范围;
的取值范围;
(2) 在曲线上取一点A,分别向 轴、
轴、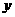 轴作垂线段,垂足分别为B、C,坐标原
轴作垂线段,垂足分别为B、C,坐标原
点为O,若四边形ABOC面积为6,求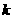 的值.
的值.
[关键词]反比例函数性质
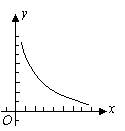
3.(2009年天津市)已知图中的曲线是反比例函数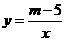 (
( 为常数)图象的一支.
为常数)图象的一支.
(Ⅰ) 这个反比例函数图象的另一支在第几象限?常数 的取值范围是什么?
的取值范围是什么?
(Ⅱ)若该函数的图象与正比例函数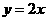 的图象在第一象内限的交点为
的图象在第一象内限的交点为 ,过
,过 点作
点作 轴的垂线,垂足为
轴的垂线,垂足为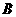 ,当
,当 的面积为4时,求点
的面积为4时,求点 的坐标及反比例函数的解析式.
的坐标及反比例函数的解析式.

2.(2009年嘉兴市)如图,曲线C是函数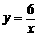 在第一象限内的图象,抛物线是函数
在第一象限内的图象,抛物线是函数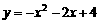 的图象.点
的图象.点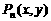 (
(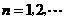 )在曲线C上,且
)在曲线C上,且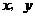 都是整数.
都是整数.
(1)求出所有的点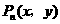 ;
;
(2)在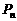 中任取两点作直线,求所有不同直线的条数;
中任取两点作直线,求所有不同直线的条数;
(3)从(2)的所有直线中任取一条直线,求所取直线与抛物线有公共点的概率.
1. (2009河池)为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量
(2009河池)为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量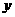 (毫克)与时间
(毫克)与时间 (分钟)成正比例;药物释放完毕后,
(分钟)成正比例;药物释放完毕后, 与
与 成反比例,如图9所示.根据图中提供的信息,解答下列问题:
成反比例,如图9所示.根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,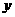 与
与 之间的两个函数
之间的两个函数
关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.45毫克
以下时,学生方可进入教室,那么从药物释放开始,
至少需要经过多少小时后,学生才能进入教室?
26.(2009成都)如图,正方形OABC的面积是4,点B在反比例函数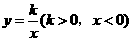 的图象上.若点R是该反比例函数图象上异于点B的任意一点,过点R分别作x轴、y轴的垂线,垂足为M、N,从矩形OMRN的面积中减去其与正方形OABC重合部分的面积,记剩余部分的面积为S.则
的图象上.若点R是该反比例函数图象上异于点B的任意一点,过点R分别作x轴、y轴的垂线,垂足为M、N,从矩形OMRN的面积中减去其与正方形OABC重合部分的面积,记剩余部分的面积为S.则
当S=m(m为常数,且0<m<4)时,点R的坐标是________________________
(用含m的代数式表示)

[关键词]反比例函数的面积
25.(2009年黄冈市)已知点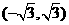 是反比例函数图象上的一点,则此反比例函数图象的解析式是____________________________.
是反比例函数图象上的一点,则此反比例函数图象的解析式是____________________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com