
题目列表(包括答案和解析)
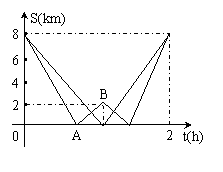
36.2009年衡阳市)在一次远足活动中,某班学生分成两组,第一组由甲地匀速步行到乙地后原路返回,第二组由甲地匀速步行经乙地继续前行到丙地后原路返回,两组同时出发,设步行的时间为t(h),两组离乙地的距离分别为S1(km)和S2(km),图中的折线分别表示S1、S2与t之间的函数关系.
(1)甲、乙两地之间的距离为 8 km,乙、丙两地之间的距离为 2 km;

 (2)求第二组由甲地出发首次到达乙地及由乙地到达丙地所用的时间分别是多少?
(2)求第二组由甲地出发首次到达乙地及由乙地到达丙地所用的时间分别是多少?
(3)求图中线段AB所表示的S2与t间的函数关系式,并写出自变量t的取值范围.

35.(2009年济宁市)在平面直角坐标中,边长为2的正方形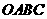 的两顶点
的两顶点 、
、 分别在
分别在 轴、
轴、 轴的正半轴上,点
轴的正半轴上,点 在原点.现将正方形
在原点.现将正方形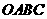 绕
绕 点顺时针旋转,当
点顺时针旋转,当 点第一次落在直线
点第一次落在直线 上时停止旋转,旋转过程中,
上时停止旋转,旋转过程中, 边交直线
边交直线 于点
于点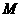 ,
, 边交
边交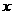 轴于点
轴于点 (如图).
(如图).
 (1)求边
(1)求边 在旋转过程中所扫过的面积;
在旋转过程中所扫过的面积;
(2)旋转过程中,当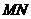 和
和 平行时,求正方形
平行时,求正方形
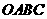 旋转的度数;
旋转的度数;
(3)设 的周长为
的周长为 ,在旋转正方形
,在旋转正方形
的过程中, 值是否有变化?请证明你的结论.
值是否有变化?请证明你的结论.
33.(2009年广州市)如图11,在方格纸上建立平面直角坐标系,线段AB的两个端点都在格点上,直线MN经过坐标原点,且点M的坐标是(1,2)。
(1)写出点A、B的坐标;
(2)求直线MN所对应的函数关系式;
(3)利用尺规作出线段AB关于直线MN的对称图形(保留作图痕迹,不写作法)。

[答案]
32.(2009年安徽)已知某种水果的批发单价与批发量的函数关系如图(1)所示.
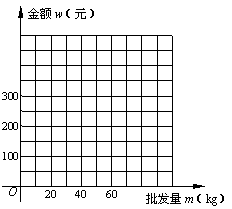 (1)请说明图中①、②两段函数图象的实际意义.
(1)请说明图中①、②两段函数图象的实际意义.
[解]

 (2)写出批发该种水果的资金金额w(元)与批发量m(kg)之间的
(2)写出批发该种水果的资金金额w(元)与批发量m(kg)之间的
函数关系式;在下图的坐标系中画出该函数图象;指出金额在什
么范围内,以同样的资金可以批发到较多数量的该种水果.
(3)经调查,某经销商销售该种水果的日最高销量与零售价之间的函
数关系如图(2)所示,该经销商拟每日售出60kg以上该种水果,
且当日零售价不变,请你帮助该经销商设计进货和销售的方案,
使得当日获得的利润最大.
31. (2009年锦州)某商场购进一批单价为50元的商品,规定销售时单价不低于进价,每件的利润不超过40%.其中销售量y(件)与所售单价x(元)的关系可以近似的看作如图12所表示的一次函数.
(1)求y与x之间的函数关系式,并求出x的取值范围;
(2)设该公司获得的总利润(总利润=总销售额-总成本)为w元,求w与x之间的函数关系式.当销售单价为何值时,所获利润最大?最大利润是多少?
30.(2009年长春)如图,直线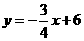 分别与
分别与 轴、
轴、 轴交于
轴交于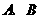 两点,直线
两点,直线 与
与 交于点
交于点 ,与过点
,与过点 且平行于
且平行于 轴的直线交于点
轴的直线交于点 .点
.点 从点
从点 出发,以每秒1个单位的速度沿
出发,以每秒1个单位的速度沿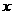 轴向左运动.过点
轴向左运动.过点 作
作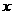 轴的垂线,分别交直线
轴的垂线,分别交直线 于
于 两点,以
两点,以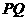 为边向右作正方形
为边向右作正方形 ,设正方形
,设正方形 与
与 重叠部分(阴影部分)的面积为
重叠部分(阴影部分)的面积为 (平方单位).点
(平方单位).点 的运动时间为
的运动时间为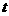 (秒).
(秒).
(1)求点 的坐标.(1分)
的坐标.(1分)
(2)当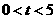 时,求
时,求 与
与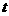 之间的函数关系式.(4分)
之间的函数关系式.(4分)
(3)求(2)中 的最大值.(2分)
的最大值.(2分)
(4)当 时,直接写出点
时,直接写出点 在正方形
在正方形 内部时
内部时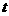 的取值范围.(3分)
的取值范围.(3分)
[参考公式:二次函数 图象的顶点坐标为
图象的顶点坐标为 .]
.]
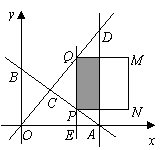
29. (2009年长春)某部队甲、乙两班参加植树活动.乙班先植树30棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为
(2009年长春)某部队甲、乙两班参加植树活动.乙班先植树30棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为 (棵),乙班植树的总量为
(棵),乙班植树的总量为 (棵),两班一起植树所用的时间(从甲班开始植树时计时)为
(棵),两班一起植树所用的时间(从甲班开始植树时计时)为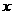 (时),
(时), 、
、 分别与
分别与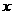 之间的部分函数图象如图所示.
之间的部分函数图象如图所示.
(1)当 时,分别求
时,分别求 、
、 与
与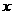 之间的函数关系式.(3分)
之间的函数关系式.(3分)
(2)如果甲、乙两班均保持前6个小时的工作效率,通过计算说明,当 时,甲、乙两班植树的总量之和能否超过260棵.(3分)
时,甲、乙两班植树的总量之和能否超过260棵.(3分)
(3)如果6个小时后,甲班保持前6个小时的工作效率,乙班通过增加人数,提高了工作效率,这样继续植树2小时,活动结束.当 时,两班之间植树的总量相差20棵,求乙班增加人数后平均每小时植树多少棵.(4分)
时,两班之间植树的总量相差20棵,求乙班增加人数后平均每小时植树多少棵.(4分)
28.(2009年牡丹江)某冰箱厂为响应国家“家电下乡”号召,计划生产 、
、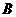 两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于 4.75万元,不高于4.8万元,两种型号的冰箱生产成本和售价如下表:
两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于 4.75万元,不高于4.8万元,两种型号的冰箱生产成本和售价如下表:
|
型号 |
A型 |
B型 |
|
成本(元/台) |
2200 |
2600 |
|
售价(元/台) |
2800 |
3000 |
(1)冰箱厂有哪几种生产方案?
(2)该冰箱厂按哪种方案生产,才能使投入成本最少?“家电下乡”后农民买家电(冰箱、彩电、洗衣机)可享受13%的政府补贴,那么在这种方案下政府需补贴给农民多少元?
(3)若按(2)中的方案生产,冰箱厂计划将获得的全部利润购买三种物品:体育器材、实验设备、办公用品支援某希望小学.其中体育器材至多买4套,体育器材每套6000元,实验设备每套3000元,办公用品每套1800元,把钱全部用尽且三种物品都购买的情况下,请你直接写出实验设备的买法共有多少种.
27. (2009年牡丹江)甲、乙两车同时从
(2009年牡丹江)甲、乙两车同时从 地出发,以各自的速度匀速向
地出发,以各自的速度匀速向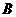 地行驶.甲车先到达
地行驶.甲车先到达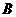 地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.下图是两车之间的距离
地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.下图是两车之间的距离 (千米)与乙车行驶时间
(千米)与乙车行驶时间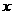 (小时)之间的函数图象.
(小时)之间的函数图象.
(1)请将图中的( )内填上正确的值,并直接写出甲车从 到
到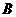 的行驶速度;
的行驶速度;
(2)求从甲车返回到与乙车相遇过程中 与
与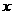 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量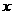 的取值范围.
的取值范围.
(3)求出甲车返回时行驶速度及 、
、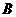 两地的距离.
两地的距离.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com