
题目列表(包括答案和解析)
1.2 一元二次方程的算法(3)公式法 同步练习
考标要求:1会用求根公式解一元二次方程;
2 会利用一元二次方程的判别式判断一元二次方程根的情况;
3 会选择适当的方法解一元二次方程;
重点:求根公式的推导过程,和用求根公式解一元二次方程;
难点:求根公式的推导过程和选择合适的方法解一元二次方程。
一 选择题(每小题5分,共25分)
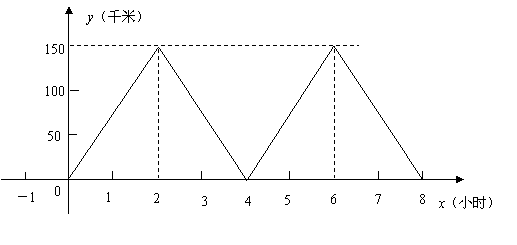
1一元二次方程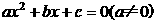 求根公式是( )
求根公式是( )
A 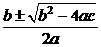 B
B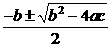
C
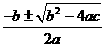 D
D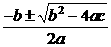 (
(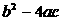 ≥0)
≥0)
2 方程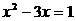 的判别式
的判别式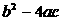 =( )
=( )
A 5 B 13 C -13 D -5
3关于x的方程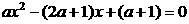 的根的情况下面说法正确的是( )
的根的情况下面说法正确的是( )
A 有两个不相等的实数根 B 没有实数根,C 有两个相等的实数根 D 当a=0时,方程有一个实数根,当a≠0时,方程有两个不相等的实数根。
4 解一元二次方程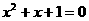 最合适的方法是( )
最合适的方法是( )
A 直接开平方法 B 因式分解法 C 配方法 D 公式法
5若2x+1与x-2互为倒数,则实数x=( )
A 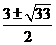 B
B 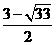 C
C 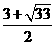 D
D 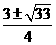
二 填空题(每小题5分,共25分)
6 已知y=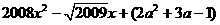 ,当x=0时,y=0,则a=_____;
,当x=0时,y=0,则a=_____;
7 x为_____时,分式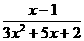 没有意义;
没有意义;
8 已知关于x的方程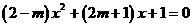 有两个相等的实数解,则m=______;
有两个相等的实数解,则m=______;
9 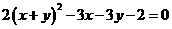 ,则x+y=_______
,则x+y=_______
10 点P在函数y=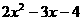 的图象上,且P的纵坐标为1 ,那么P点的横坐标为_____
的图象上,且P的纵坐标为1 ,那么P点的横坐标为_____
三 解答题(第11题20分,12题9分,13题5分,14、15各8分)
11 用公式法解下列方程
(1) 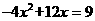 (2)(x-1)(2x+1)=2
(2)(x-1)(2x+1)=2
(3) 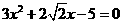 (4)
(4)
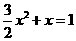
12 用适当的方法解下列方程
(1)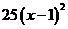 =36 (2)
=36 (2) 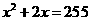 (3)
(3) 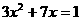
13 已知a、b、c是△ABC的三边长,且方程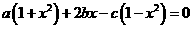 有相等的两个实数根,试判断△ABC的形状。
有相等的两个实数根,试判断△ABC的形状。
14 一个人拿一根竹竿前行,横放比门长3m,竖放比门高2m,沿门对角线斜放还长1m,那么这根竹竿有多长,门的宽和高分别为多少?
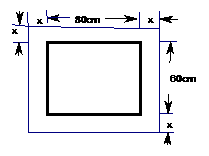 15在一副长为60cm,宽为80cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使挂图的面积为6300
15在一副长为60cm,宽为80cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使挂图的面积为6300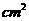 ,求金色纸边的宽。
,求金色纸边的宽。
45.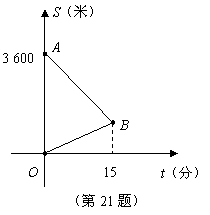 (2009江西)某天,小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.下图中线段
(2009江西)某天,小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.下图中线段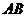 、
、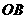 分别表示父、子俩送票、取票过程中,离体育馆的路程
分别表示父、子俩送票、取票过程中,离体育馆的路程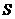 (米)与所用时间
(米)与所用时间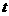 (分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(1)求点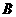 的坐标和
的坐标和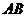 所在直线的函数关系式;
所在直线的函数关系式;
(2)小明能否在比赛开始前到达体育馆?
44.(2009泰安)如图,△OAB是边长为2的等边三角形,过点A的直线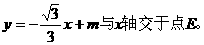
(1) 求点E的坐标;
(2) 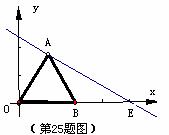 求过 A、O、E三点的抛物线解析式;
求过 A、O、E三点的抛物线解析式;
(3) 若点P是(2)中求出的抛物线AE段上一动点(不与A、E重合),设四边形OAPE的面积为S,求S的最大值。
43.(2009年牡丹江市)甲、乙两车同时从 地出发,以各自的速度匀速向
地出发,以各自的速度匀速向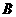 地行驶.甲车先到达
地行驶.甲车先到达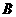 地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.下图是两车之间的距离
地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.下图是两车之间的距离 (千米)与乙车行驶时间
(千米)与乙车行驶时间 (小时)之间的函数图象.
(小时)之间的函数图象.
(1)请将图中的( )内填上正确的值,并直接写出甲车从 到
到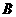 的行驶速度;
的行驶速度;
(2)求从甲车返回到与乙车相遇过程中 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围.
的取值范围.
(3)求出甲车返回时行驶速度及 、
、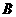 两地的距离.
两地的距离.
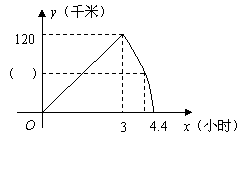

42.(2009年新疆)某公交公司的公共汽车和出租车每天从乌鲁木齐市出发往返于乌鲁木齐市和石河子市两地,出租车比公共汽车多往返一趟,如图表示出租车距乌鲁木齐市的路程 (单位:千米)与所用时间
(单位:千米)与所用时间 (单位:小时)的函数图象.已知公共汽车比出租车晚1小时出发,到达石河子市后休息2小时,然后按原路原速返回,结果比出租车最后一次返回乌鲁木齐早1小时.
(单位:小时)的函数图象.已知公共汽车比出租车晚1小时出发,到达石河子市后休息2小时,然后按原路原速返回,结果比出租车最后一次返回乌鲁木齐早1小时.
(1)请在图中画出公共汽车距乌鲁木齐市的路程 (千米)与所用时间
(千米)与所用时间 (小时)的函数图象.
(小时)的函数图象.
(2)求两车在途中相遇的次数(直接写出答案)
(3)求两车最后一次相遇时,距乌鲁木齐市的路程.

41.(2009白银市)23.鞋子的“鞋码”和鞋长(cm)存在一种换算关系,下表是几组“鞋码”与鞋长换算的对应数值:[注:“鞋码”是表示鞋子大小的一种号码]
|
鞋长(cm) |
16 |
19 |
21 |
24 |
|
鞋码(号) |
22 |
28 |
32 |
38 |
(1)设鞋长为x,“鞋码”为y,试判断点(x,y)在你学过的哪种函数的图象上?
(2)求x、y之间的函数关系式;
(3)如果某人穿44号“鞋码”的鞋,那么他的鞋长是多少?
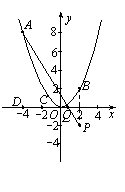
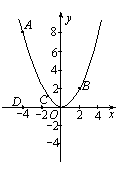
40.(2009年舟山)如图,已知点A(-4,8)和点B(2,n)在抛物线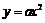 上.
上.
(1) 求a的值及点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求出点Q的坐标;
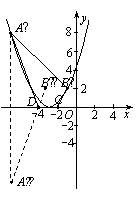
(2) 平移抛物线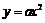 ,记平移后点A的对应点为A′,点B的对应点为B′,点C(-2,0)和点D(-4,0)是x轴上的两个定点.
,记平移后点A的对应点为A′,点B的对应点为B′,点C(-2,0)和点D(-4,0)是x轴上的两个定点.
① 当抛物线向左平移到某个位置时,A′C+CB′ 最短,求此时抛物线的函数解析式;
② 当抛物线向左或向右平移时,是否存在某个位置,使四边形A′B′CD的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.

39.(2009年衢州)(如图,已知点A(-4,8)和点B(2,n)在抛物线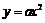 上.
上.
(1) 求a的值及点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求出点Q的坐标;
(2) 平移抛物线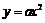 ,记平移后点A的对应点为A′,点B的对应点为B′,点C(-2,0)和点D(-4,0)是x轴上的两个定点.
,记平移后点A的对应点为A′,点B的对应点为B′,点C(-2,0)和点D(-4,0)是x轴上的两个定点.
① 当抛物线向左平移到某个位置时,A′C+CB′ 最短,求此时抛物线的函数解析式;
② 当抛物线向左或向右平移时,是否存在某个位置,使四边形A′B′CD的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.


38.(2009年清远)某饮料厂为了开发新产品,用 种果汁原料和
种果汁原料和 种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制
种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制 千克,两种饮料的成本总额为
千克,两种饮料的成本总额为 元.
元.
(1)已知甲种饮料成本每千克4元,乙种饮料成本每千克3元,请你写出 与
与 之间的函数关系式.
之间的函数关系式.
(2)若用19千克 种果汁原料和17.2千克
种果汁原料和17.2千克 种果汁原料试制甲、乙两种新型饮料,下表是试验的相关数据;
种果汁原料试制甲、乙两种新型饮料,下表是试验的相关数据;
 每千克饮料 每千克饮料果汁含量 果汁 |
甲 |
乙 |
|
A |
0.5千克 |
0.2千克 |
|
B |
0.3千克 |
0.4千克 |
请你列出关于 且满足题意的不等式组,求出它的解集,并由此分析如何配制这两种饮料,可使
且满足题意的不等式组,求出它的解集,并由此分析如何配制这两种饮料,可使 值最小,最小值是多少?
值最小,最小值是多少?
37.(2009年衡阳市)如图,直线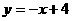 与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
(1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(2)当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?
(3)当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向移动,设平移的距离为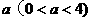 ,正方形OCMD与△AOB重叠部分的面积为S.试求S与
,正方形OCMD与△AOB重叠部分的面积为S.试求S与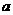 的函数关系式并画出该函数的图象.
的函数关系式并画出该函数的图象.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com