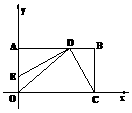
43.　　 (2009重庆) (2009重庆已知：如图，在平面直角坐标系中，矩形OABC的边OA在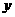轴的正半轴上，OC在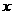轴的正半轴上，OA=2，OC=3。过原点O作∠AOC的平分线交AB于点D，连接DC，过点D作DE⊥DC，交OA于点E。

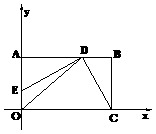(1)求过点E、D、C的抛物线的解析式；

(2)将∠EDC绕点D按顺时针方向旋转后，角的一边与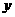轴的正半轴交于点F，另一边与线段OC交于点G。如果DF与(1)中的抛物线交于另一点M，点M的横坐标为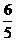，那么EF=2GO是否成立？若成立，请给予证明；若不成立，请说明理由；

(3)对于(2)中的点G，在位于第一象限内的该抛物线上是否存在点Q，使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由。

42.　　 (2009重庆) (2009重庆已知：如图，在平面直角坐标系中，矩形OABC的边OA在轴的正半轴上，OC在轴的正半轴上，OA=2，OC=3。过原点O作∠AOC的平分线交AB于点D，连接DC，过点D作DE⊥DC，交OA于点E。

(1)求过点E、D、C的抛物线的解析式；

(2)将∠EDC绕点D按顺时针方向旋转后，角的一边与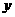轴的正半轴交于点F，另一边与线段OC交于点G。如果DF与(1)中的抛物线交于另一点M，点M的横坐标为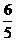，那么EF=2GO是否成立？若成立，请给予证明；若不成立，请说明理由；

(3)对于(2)中的点G，在位于第一象限内的该抛物线上是否存在点Q，使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由。

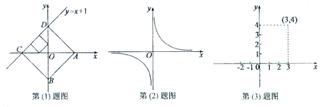
41.　　 (2009义乌)已知点A、B分别是轴、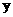轴上的动点，点C、D是某个函数图像上的点，当四边形ABCD(A、B、C、D各点依次排列)为正方形时，称这个正方形为此函数图像的伴侣正方形。例如：如图，正方形ABCD是一次函数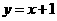图像的其中一个伴侣正方形。

(1)若某函数是一次函数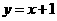，求它的图像的所有伴侣正方形的边长；

(2)若某函数是反比例函数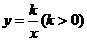，他的图像的伴侣正方形为ABCD，点D(2，m)(m <2)在反比例函数图像上，求m的值及反比例函数解析式；

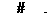(3)若某函数是二次函数，它的图像的伴侣正方形为ABCD，C、D中的一个点坐标为(3，4).写出伴侣正方形在抛物线上的另一个顶点坐标，写出符合题意的其中一条抛物线解析式，并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数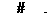？。(本小题只需直接写出答案)

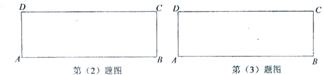
40.　　 (2009义乌)如图，在矩形ABCD中，AB=3,AD=1,点P在线段AB上运动，设AP=，现将纸片折叠，使点D与点P重合，得折痕EF(点E、F为折痕与矩形边的交点)，再将纸片还原。

　 (1)当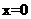时，折痕EF的长为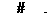；当点E与点A重合时，折痕EF的长为；

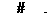(2)请写出使四边形EPFD为菱形的的取值范围，并求出当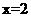时菱形的边长；

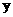(3)令，当点E在AD、点F在BC上时，写出与的函数关系式。当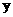取最大值时，判断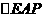与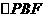是否相似？若相似，求出的值；若不相似，请说明理由。

温馨提示：用草稿纸折折看，或许对你有所帮助哦！

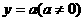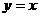39.　　 (2009杭州)已知平行于x轴的直线与函数和函数的图象分别交于点A和点B，又有定点P(2，0)。

(1)若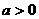，且tan∠POB=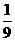，求线段AB的长；

(2)在过A，B两点且顶点在直线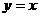上的抛物线中，已知线段AB=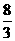，且在它的对称轴左边时，y随着x的增大而增大，试求出满足条件的抛物线的解析式；

(3)已知经过A，B，P三点的抛物线，平移后能得到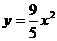的图象，求点P到直线AB的距离。

38.　　 (13分)(2009洛江)我区某工艺厂为迎接建国60周年，设计了一款成本为20元 ∕ 件的工艺品投放市场进行试销．经过调查，其中工艺品的销售单价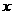(元 ∕ 件)与每天销售量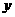(件)之间满足如图所示关系．

(1)请根据图象直接写出当销售单价定为30元和

40元时相应的日销售量；

(2)①试求出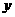与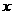之间的函数关系式；

②若物价部门规定，该工艺品销售单价最高不能超过45元/件，那么销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？最大利润是多少？(利润=销售总价－成本总价)。(2009日照)某仓库为了保持库内的湿度和温度，四周墙上均装有如图所示的自动通风设施．该设施的下部ABCD是矩形，其中AB=2米，BC=1米；上部CDG是等边三角形，固定点E为AB的中点．△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风)，MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆．

(1)当MN和AB之间的距离为0.5米时，求此时△EMN的面积；

(2)设MN与AB之间的距离为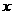米，试将△EMN的面积S(平方米)表示成关于x的函数；　

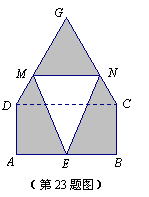(3)请你探究△EMN的面积S(平方米)有无最大值，若有，请求出这个最大值；若没有，请说明理由．　

37.　　 (2009荆门)一开口向上的抛物线与x轴交于A(m－2，0)，B(m+2，0)两点，记抛物线顶点为C，且AC⊥BC．

(1)若m为常数，求抛物线的解析式；

(2)若m为小于0的常数，那么(1)中的抛物线经过怎么样的平移可以使顶点在坐标原点？

(3)设抛物线交y轴正半轴于D点，问是否存在实数m，使得△BCD为等腰三角形？若存在，求出m的值；若不存在，请说明理由．

36.　　 (2009中山)正方形ABCD边长为4，M、N分别是BC、CD上的两个动点，当M点在BC上运动时，保持AM和MN垂直.

(1)证明：Rt△ABM∽Rt△MCN；

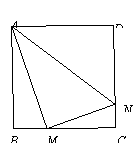(2)设BM=x，梯形ABCN的面积为y，求y与x之间的函数关系式；当M点运动到什么位置时，四边形ABCN面积最大，并求出最大面积；

(3)当M点运动到什么位置时Rt△ABM∽Rt△AMN，求此时x的值.

35.　　 (2009娄底)已知关于x的二次函数y=x²-(2m-1)x+m²+3m+4.　

(1)探究m满足什么条件时，二次函数y的图象与x轴的交点的个数.　

(2)设二次函数y的图象与x轴的交点为A(x₁，0)，B(x₂，0)，且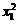+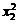=5，与y轴的交点为C，它的顶点为M，求直线CM的解析式.

34.　　 (2009烟台) 某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施.调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台．

　 (1)假设每台冰箱降价x元，商场每天销售这种冰箱的利润是y元，请写出y与x之间的函数表达式；(不要求写自变量的取值范围)

　 (2)商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？

　 (3)每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？