
题目列表(包括答案和解析)
93.(2009年四川资阳)25. 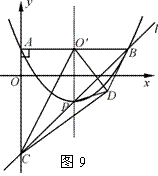 如图9,已知抛物线y=
如图9,已知抛物线y=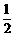 x2–2x+1的顶点为P,A为抛物线与y轴的交点,过A与y轴垂直的直线与抛物线的另一交点为B,与抛物线对称轴交于点O′,过点B和P的直线l交y轴于点C,连结O′C,将△ACO′沿O′C翻折后,点A落在点D的位置.
x2–2x+1的顶点为P,A为抛物线与y轴的交点,过A与y轴垂直的直线与抛物线的另一交点为B,与抛物线对称轴交于点O′,过点B和P的直线l交y轴于点C,连结O′C,将△ACO′沿O′C翻折后,点A落在点D的位置.
(1) (3分) 求直线l的函数解析式;
(2) (3分) 求点D的坐标;
(3) (3分) 抛物线上是否存在点Q,使得S△DQC= S△DPB? 若存在,求出所有符合条件的点Q的坐标;若不存在,请说明理由.
(2009年四川资阳25题解析)
(1) 配方,得y=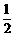 (x–2)2 –1,∴抛物线的对称轴为直线x=2,顶点为P(2,–1) .··············· 1分
(x–2)2 –1,∴抛物线的对称轴为直线x=2,顶点为P(2,–1) .··············· 1分
取x=0代入y=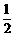 x2
–2x+1,得y=1,∴点A的坐标是(0,1).由抛物线的对称性知,点A(0,1)与点B关于直线x=2对称,∴点B的坐标是(4,1).··························································································· 2分
x2
–2x+1,得y=1,∴点A的坐标是(0,1).由抛物线的对称性知,点A(0,1)与点B关于直线x=2对称,∴点B的坐标是(4,1).··························································································· 2分
设直线l的解析式为y=kx+b(k≠0),将B、P的坐标代入,有
 解得
解得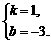 ∴直线l的解析式为y=x–3.·············································· 3分
∴直线l的解析式为y=x–3.·············································· 3分
(2) 连结AD交O′C于点E,∵ 点D由点A沿O′C翻折后得到,∴ O′C垂直平分AD.
由(1)知,点C的坐标为(0,–3),∴ 在Rt△AO′C中,O′A=2,AC=4,∴ O′C=2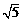 .
.
据面积关系,有 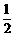 ×O′C×AE=
×O′C×AE=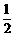 ×O′A×CA,∴ AE=
×O′A×CA,∴ AE=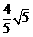 ,AD=2AE=
,AD=2AE=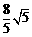 .
.
作DF⊥AB于F,易证Rt△ADF∽Rt△CO′A,∴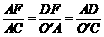 ,
,
∴ AF=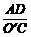 ·AC=
·AC=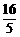 ,DF=
,DF=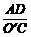 ·O′A=
·O′A=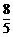 ,································································ 5分
,································································ 5分
又 ∵OA=1,∴点D的纵坐标为1–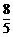 = –
= – ,∴ 点D的坐标为(
,∴ 点D的坐标为(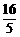 ,–
,– ).·············· 6分
).·············· 6分
(3) 显然,O′P∥AC,且O′为AB的中点,
∴ 点P是线段BC的中点,∴ S△DPC= S△DPB .
故要使S△DQC= S△DPB,只需S△DQC=S△DPC .
··············································································· 7分
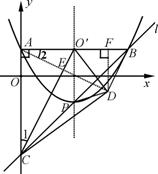 过P作直线m与CD平行,则直线m上的任意一点与CD构成的三角形的面积都等于S△DPC ,故m与抛物线的交点即符合条件的Q点.
过P作直线m与CD平行,则直线m上的任意一点与CD构成的三角形的面积都等于S△DPC ,故m与抛物线的交点即符合条件的Q点.
容易求得过点C(0,–3)、D(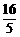 ,–
,– )的直线的解析式为y=
)的直线的解析式为y=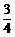 x–3,
x–3,
据直线m的作法,可以求得直线m的解析式为y=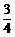 x–
x–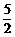 .
.
令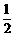 x2–2x+1=
x2–2x+1=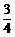 x–
x–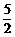 ,解得 x1=2,x2=
,解得 x1=2,x2=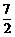 ,代入y=
,代入y=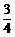 x–
x–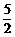 ,得y1= –1,y2=
,得y1= –1,y2=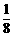 ,
,
因此,抛物线上存在两点Q1(2,–1)(即点P)和Q2(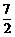 ,
,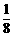 ),使得S△DQC=
S△DPB.····· 9分
),使得S△DQC=
S△DPB.····· 9分
(仅求出一个符合条件的点Q的坐标,扣1分)
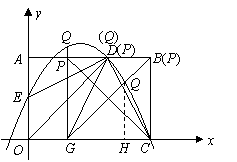
92.(2009年重庆)26.已知:如图,在平面直角坐标系 中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=2,OC=3.过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E.
中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=2,OC=3.过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E.
(1)求过点E、D、C的抛物线的解析式;
(2)将∠EDC绕点D按顺时针方向旋转后,角的一边与y轴的正半轴交于点F,另一边与线段OC交于点G.如果DF与(1)中的抛物线交于另一点M,点M的横坐标为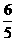 ,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
(3)对于(2)中的点G,在位于第一象限内的该抛物线上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.

(2009年重庆26题解析)解:(1)由已知,得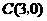 ,
,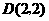 ,
,
 ,
,
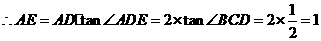 .
.

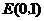 .············································································································ (1分)
.············································································································ (1分)
设过点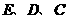 的抛物线的解析式为
的抛物线的解析式为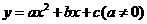 .
.
将点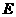 的坐标代入,得
的坐标代入,得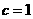 .
.
将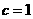 和点
和点 的坐标分别代入,得
的坐标分别代入,得
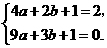 ··································································································· (2分)
··································································································· (2分)
解这个方程组,得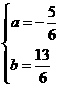
故抛物线的解析式为 .··························································· (3分)
.··························································· (3分)
(2)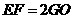 成立.························································································· (4分)
成立.························································································· (4分)
 点
点 在该抛物线上,且它的横坐标为
在该抛物线上,且它的横坐标为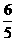 ,
,
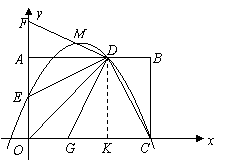
 点
点 的纵坐标为
的纵坐标为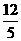 .······················································································· (5分)
.······················································································· (5分)
设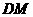 的解析式为
的解析式为 ,
,
将点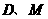 的坐标分别代入,得
的坐标分别代入,得
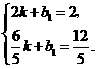 解得
解得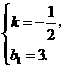

 的解析式为
的解析式为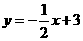 .········································································ (6分)
.········································································ (6分)

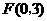 ,
,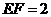 .··························································································· (7分)
.··························································································· (7分)
过点 作
作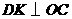 于点
于点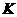 ,
,
则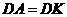 .
.
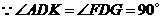 ,
,
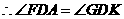 .
.
又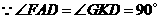 ,
,
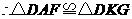 .
.
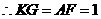 .
.
 .··········································································································· (8分)
.··········································································································· (8分)
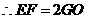 .
.
(3) 点
点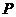 在
在 上,
上,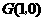 ,
,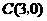 ,则设
,则设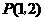 .
.

 ,
,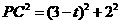 ,
,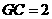 .
.
①若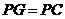 ,则
,则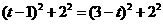 ,
,
解得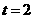 .
.
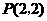 ,此时点
,此时点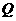 与点
与点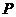 重合.
重合.

 .··········································································································· (9分)
.··········································································································· (9分)
②若 ,则
,则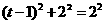 ,
,
解得 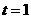 ,
,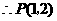 ,此时
,此时 轴.
轴.
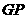 与该抛物线在第一象限内的交点
与该抛物线在第一象限内的交点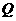 的横坐标为1,
的横坐标为1,
 点
点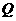 的纵坐标为
的纵坐标为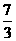 .
.

 .······································································································· (10分)
.······································································································· (10分)
 ③若
③若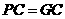 ,则
,则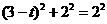 ,
,
解得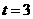 ,
, ,此时
,此时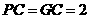 ,
,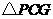 是等腰直角三角形.
是等腰直角三角形.
过点 作
作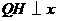 轴于点
轴于点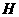 ,
,
则 ,设
,设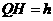 ,
,
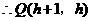 .
.
 .
.
解得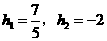 (舍去).
(舍去).
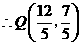 .··········································· (12分)
.··········································· (12分)
综上所述,存在三个满足条件的点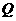 ,
,
即 或
或 或
或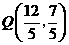 .
.
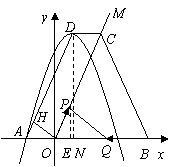
91.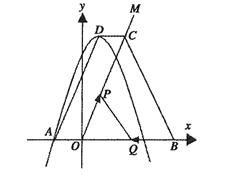 (2009年重庆綦江)26.(11分)如图,已知抛物线
(2009年重庆綦江)26.(11分)如图,已知抛物线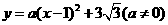 经过点A(-2,0),抛物线的顶点为D,过0作射线OM∥AD.过顶点D平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连结BC.
经过点A(-2,0),抛物线的顶点为D,过0作射线OM∥AD.过顶点D平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连结BC.
(1)求该抛物线的解析式;
(2)若动点P从点0出发,以每秒l个长度单位的速度沿射线OM运动,设点P运动的时间为t(s).问:当t为何值时,四边形DAOP分别为平行四边形?直角梯形?等腰梯形?
(3)若OC=OB,动点P和动点Q分别从点O和点B同时出发,分别以每秒l个长度单位和2个长度单位的速度沿OC和B0运动,当其中一个点停止运动时另一个点也随之停止运动设它们运动的时间为t(s),连接PQ,当t为何值时,四边形BCPQ的面积最小?并求出最小值及此时PQ的长.
(2009年重庆綦江26题解析)解:(1) 抛物线
抛物线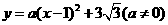 经过点
经过点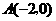 ,
,
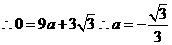 ·························································································· 1分
·························································································· 1分
 二次函数的解析式为:
二次函数的解析式为: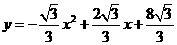 ·················································· 3分
·················································· 3分
(2) 为抛物线的顶点
为抛物线的顶点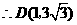 过
过 作
作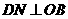 于
于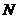 ,则
,则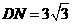 ,
,
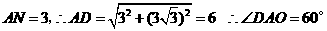 ··················································· 4分
··················································· 4分

 当
当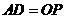 时,四边形
时,四边形 是平行四边形
是平行四边形
 ················································ 5分
················································ 5分
 当
当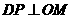 时,四边形
时,四边形 是直角梯形
是直角梯形
过 作
作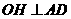 于
于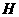 ,
, 则
则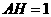
(如果没求出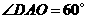 可由
可由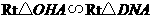 求
求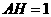 )
)
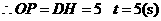 ····························································································· 6分
····························································································· 6分
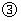 当
当 时,四边形
时,四边形 是等腰梯形
是等腰梯形
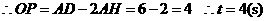
综上所述:当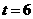 、5、4时,对应四边形分别是平行四边形、直角梯形、等腰梯形.·· 7分
、5、4时,对应四边形分别是平行四边形、直角梯形、等腰梯形.·· 7分
(3)由(2)及已知, 是等边三角形
是等边三角形
则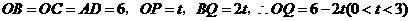
过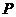 作
作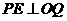 于
于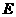 ,则
,则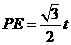 ········································································· 8分
········································································· 8分

=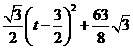 ·································································································· 9分
·································································································· 9分
当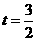 时,
时,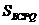 的面积最小值为
的面积最小值为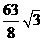 ··································································· 10分
··································································· 10分
 此时
此时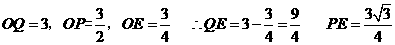
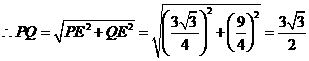 ······················································ 11分
······················································ 11分
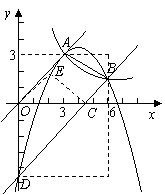
90.(2009年四川南充)21.如图9,已知正比例函数和反比例函数的图象都经过点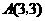 .
.
(1)求正比例函数和反比例函数的解析式;
(2)把直线OA向下平移后与反比例函数的图象交于点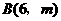 ,求
,求 的值和这个一次函数的解析式;
的值和这个一次函数的解析式;
(3)第(2)问中的一次函数的图象与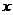 轴、
轴、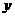 轴分别交于C、D,求过A、B、D三点的二次函数的解析式;
轴分别交于C、D,求过A、B、D三点的二次函数的解析式;
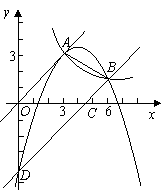 (4)在第(3)问的条件下,二次函数的图象上是否存在点E,使四边形OECD的面积
(4)在第(3)问的条件下,二次函数的图象上是否存在点E,使四边形OECD的面积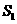 与四边形OABD的面积S满足:
与四边形OABD的面积S满足: ?若存在,求点E的坐标;若不存在,请说明理由.
?若存在,求点E的坐标;若不存在,请说明理由.
(2009年四川南充21题解析)解:(1)设正比例函数的解析式为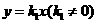 ,
,
因为 的图象过点
的图象过点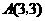 ,所以
,所以
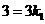 ,解得
,解得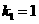 .
.
这个正比例函数的解析式为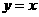 .······································································· (1分)
.······································································· (1分)
设反比例函数的解析式为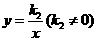 .
.
因为 的图象过点
的图象过点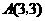 ,所以
,所以
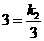 ,解得
,解得 .
.
这个反比例函数的解析式为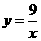 .······································································ (2分)
.······································································ (2分)
(2)因为点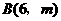 在
在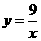 的图象上,所以
的图象上,所以
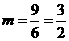 ,则点
,则点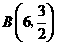 .················································································· (3分)
.················································································· (3分)
设一次函数解析式为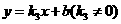 .
.
因为 的图象是由
的图象是由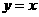 平移得到的,
平移得到的,
所以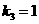 ,即
,即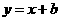 .
.
又因为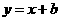 的图象过点
的图象过点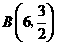 ,所以
,所以
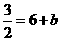 ,解得
,解得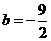 ,
,
 一次函数的解析式为
一次函数的解析式为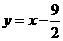 .········································································ (4分)
.········································································ (4分)
(3)因为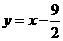 的图象交
的图象交 轴于点
轴于点 ,所以
,所以 的坐标为
的坐标为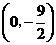 .
.
设二次函数的解析式为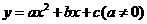 .
.
因为 的图象过点
的图象过点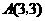 、
、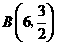 、和
、和
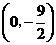 ,
,
所以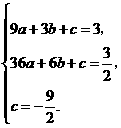 ··················· (5分)
解得
··················· (5分)
解得
这个二次函数的解析式为 .····················································· (6分)
.····················································· (6分)
(4)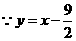 交
交 轴于点
轴于点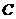 ,
, 点
点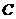 的坐标是
的坐标是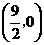 ,
,
 如图所示,
如图所示,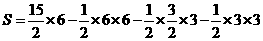
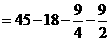
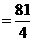 .
.
假设存在点 ,使
,使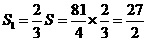 .
.
 四边形
四边形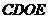 的顶点
的顶点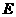 只能在
只能在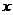 轴上方,
轴上方,
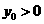 ,
,
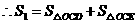

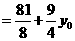 .
.
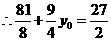 ,
,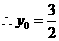 .············································································· (7分)
.············································································· (7分)
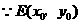 在二次函数的图象上,
在二次函数的图象上,
 .
.
解得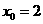 或
或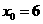 .
.
当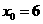 时,点
时,点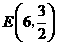 与点
与点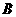 重合,这时
重合,这时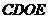 不是四边形,故
不是四边形,故 舍去,
舍去,
 点
点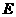 的坐标为
的坐标为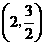 .······················································································ (8分)
.······················································································ (8分)
89.(2009年四川绵阳)25.如图,在平面直角坐标系中,矩形AOBC在第一象限内,E是边OB上的动点(不包括端点),作∠AEF = 90°,使EF交矩形的外角平分线BF于点F,设C(m,n).
(1)若m = n时,如图,求证:EF = AE;
(2)若m≠n时,如图,试问边OB上是否还存在点E,使得EF = AE?若存在,请求出点E的坐标;若不存在,请说明理由.
(3)若m = tn(t>1)时,试探究点E在边OB的何处时,使得EF =(t + 1)AE成立?并求出点E的坐标.

(2009年四川绵阳25题解析)(1)由题意得m = n时,AOBC是正方形.
如图,在OA上取点C,使AG = BE,则OG = OE.
∴ ∠EGO = 45°,从而 ∠AGE = 135°.
由BF是外角平分线,得 ∠EBF = 135°,∴ ∠AGE =∠EBF.
∵ ∠AEF = 90°,∴ ∠FEB +∠AEO = 90°.
在Rt△AEO中,∵ ∠EAO +∠AEO = 90°,
∴ ∠EAO =∠FEB,∴ △AGE≌△EBF,EF = AE.
(2)假设存在点E,使EF = AE.设E(a,0).作FH⊥x轴于H,如图.
由(1)知∠EAO =∠FEH,于是Rt△AOE≌Rt△EHF.
∴ FH = OE,EH = OA.
∴ 点F的纵坐标为a,即 FH = a.
由BF是外角平分线,知∠FBH = 45°,∴ BH = FH = a.
又由C(m,n)有OB = m,∴ BE = OB-OE = m-a,
 ∴ EH = m-a + a = m.
∴ EH = m-a + a = m.
又EH = OA = n, ∴ m = n,这与已知m≠n相矛盾.
因此在边OB上不存在点E,使EF = AE成立.
(3)如(2)图,设E(a,0),FH = h,则EH = OH-OE = h + m-a.
由 ∠AEF = 90°,∠EAO =∠FEH,得 △AOE∽△EHF,
∴ EF =(t + 1)AE等价于 FH =(t + 1)OE,即h =(t + 1)a,
且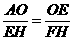 ,即
,即 ,
,
 整理得 nh = ah + am-a2,∴
整理得 nh = ah + am-a2,∴  .
.
把h =(t + 1)a 代入得 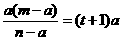 ,
,
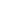 即 m-a =(t + 1)(n-a).
即 m-a =(t + 1)(n-a).
而 m = tn,因此 tn-a =(t + 1)(n-a).
化简得 ta = n,解得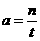 .
.
∵ t>1, ∴ 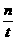 <n<m,故E在OB边上.
<n<m,故E在OB边上.
∴当E在OB边上且离原点距离为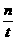 处时满足条件,此时E(
处时满足条件,此时E(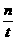 ,0).
,0).
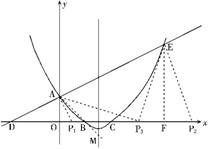
88.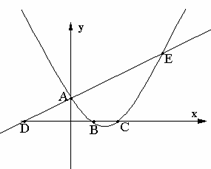 (2009年四川眉山)24.如图,已知直线
(2009年四川眉山)24.如图,已知直线 与
与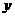 轴交于点A,与
轴交于点A,与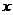 轴交于点D,抛物线
轴交于点D,抛物线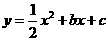 与直线交于A、E两点,与
与直线交于A、E两点,与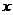 轴交于B、C两点,且B点坐标为 (1,0)。
轴交于B、C两点,且B点坐标为 (1,0)。
⑴求该抛物线的解析式;
⑵动点P在轴上移动,当△PAE是直角三角形时,求点P的坐标P。
⑶在抛物线的对称轴上找一点M,使 的值最大,求出点M的坐标。
的值最大,求出点M的坐标。
(2009年四川眉山24题解析)(1)将A(0,1)、B(1,0)坐标代入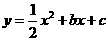 得
得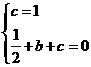 解得
解得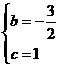
∴抛物线的解折式为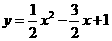 …(2分)
…(2分)
 (2)设点E的横坐标为m,则它的纵坐标为
(2)设点E的横坐标为m,则它的纵坐标为 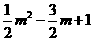
即 E点的坐标( ,
,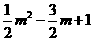 )又∵点E在直线
)又∵点E在直线 上
上
∴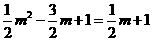 解得
解得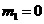 (舍去),
(舍去),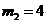
∴E的坐标为(4,3)……(4分)
(Ⅰ)当A为直角顶点时
过A作AP1⊥DE交x轴于P1点,设P1(a,0) 易知D点坐标为(-2,0) 由Rt△AOD∽Rt△POA得
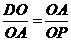 即
即 ,∴a=
,∴a=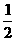 ∴P1(
∴P1(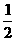 ,0)……(5分)
,0)……(5分)
(Ⅱ)同理,当E为直角顶点时,P2点坐标为(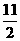 ,0)……(6分)
,0)……(6分)
(Ⅲ)当P为直角顶点时,过E作EF⊥x轴于F,设P3( 、
、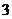 )由∠OPA+∠FPE=90°,得∠OPA=∠FEP Rt△AOP∽Rt△PFE
)由∠OPA+∠FPE=90°,得∠OPA=∠FEP Rt△AOP∽Rt△PFE
由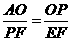 得
得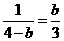 解得
解得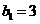 ,
,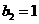
∴此时的点P3的坐标为(1,0)或(3,0)……(8分)
综上所述,满足条件的点P的坐标为(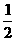 ,0)或(1,0)或(3,0)或(
,0)或(1,0)或(3,0)或(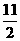 ,0)
,0)
(Ⅲ)抛物线的对称轴为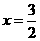 …(9分)∵B、C关于x=
…(9分)∵B、C关于x=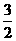 对称 ∴MC=MB
对称 ∴MC=MB
要使 最大,即是使
最大,即是使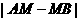 最大
最大
由三角形两边之差小于第三边得,当A、B、M在同一直线上时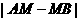 的值最大.(10分)
的值最大.(10分)
易知直线AB的解折式为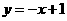 ∴由
∴由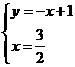 得
得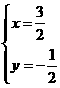 ∴M(
∴M(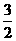 ,-
,-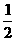 )……(11分)
)……(11分)
87.(2009年四川凉山州)26.如图,已知抛物线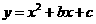 经过
经过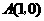 ,
, 两点,顶点为
两点,顶点为 .
.
(1)求抛物线的解析式;
(2)将 绕点
绕点 顺时针旋转90°后,点
顺时针旋转90°后,点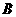 落到点
落到点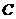 的位置,将抛物线沿
的位置,将抛物线沿 轴平移后经过点
轴平移后经过点 ,求平移后所得图象的函数关系式;
,求平移后所得图象的函数关系式;
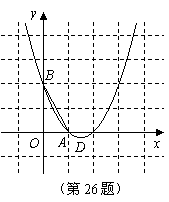 (3)设(2)中平移后,所得抛物线与
(3)设(2)中平移后,所得抛物线与 轴的交点为
轴的交点为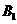 ,顶点为
,顶点为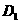 ,若点
,若点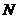 在平移后的抛物线上,且满足
在平移后的抛物线上,且满足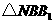 的面积是
的面积是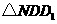 面积的2倍,求点
面积的2倍,求点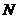 的坐标.
的坐标.
(2009年四川凉山州26题解析)解:(1)已知抛物线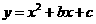 经过
经过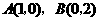 ,
,
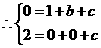 解得
解得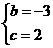
 所求抛物线的解析式为
所求抛物线的解析式为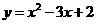 .··································································· 2分
.··································································· 2分
(2)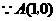 ,
, ,
,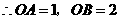
可得旋转后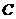 点的坐标为
点的坐标为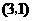 ······················································································ 3分
······················································································ 3分
当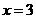 时,由
时,由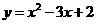 得
得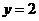 ,
,
可知抛物线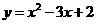 过点
过点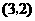
 将原抛物线沿
将原抛物线沿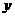 轴向下平移1个单位后过点
轴向下平移1个单位后过点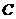 .
.
 平移后的抛物线解析式为:
平移后的抛物线解析式为: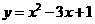 .···························································· 5分
.···························································· 5分
(3) 点
点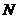 在
在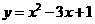 上,可设
上,可设 点坐标为
点坐标为
将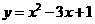 配方得
配方得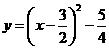 ,
, 其对称轴为
其对称轴为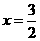 .······························ 6分
.······························ 6分
 ①当
①当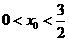 时,如图①,
时,如图①,
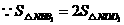
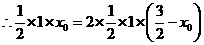
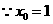
此时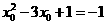
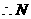 点的坐标为
点的坐标为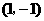 .····························································································· 8分
.····························································································· 8分
 ②当
②当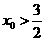 时,如图②
时,如图②
同理可得
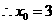
此时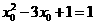
 点
点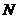 的坐标为
的坐标为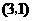 .
.
综上,点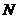 的坐标为
的坐标为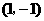 或
或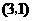 .········································································· 10分
.········································································· 10分
86.(2009年四川成都)28.在平面直角坐标系xOy中,已知抛物线y=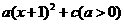 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,其顶点为M,若直线MC的函数表达式为
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,其顶点为M,若直线MC的函数表达式为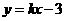 ,与x轴的交点为N,且COS∠BCO=
,与x轴的交点为N,且COS∠BCO= 。
。
(1)求此抛物线的函数表达式;
(2)在此抛物线上是否存在异于点C的点P,使以N、P、C为顶点的三角形是以NC为一条直角边的直角三角形?若存在,求出点P的坐标:若不存在,请说明理由;
(3)过点A作x轴的垂线,交直线MC于点Q.若将抛物线沿其对称轴上下平移,使抛物线与线段NQ总有公共点,则抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
(2009年四川成都28题解析)

85.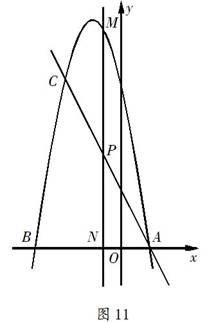 (2009年四川达州)23、(9分)如图11,抛物线
(2009年四川达州)23、(9分)如图11,抛物线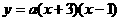 与
与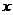 轴相交于A、B两点(点A在点B右侧),过点A的直线交抛物线于另一点C,点C的坐标为(-2,6).
轴相交于A、B两点(点A在点B右侧),过点A的直线交抛物线于另一点C,点C的坐标为(-2,6).
(1)求a的值及直线AC的函数关系式;
(2)P是线段AC上一动点,过点P作y轴的平行线,交抛物线于点M,交x轴于点N.
①求线段PM长度的最大值;
②在抛物线上是否存在这样的点M,使得△CMP与△APN相似?如果存在,请直接写出所有满足条件的点M的坐标(不必写解答过程);如果不存在,请说明理由.
(2009年四川达州23题解析)解:(1)由题意得 6=a(-2+3)(-2-1)∴a=-21分
∴抛物线的函数解析式为y=-2(x+3)(x-1)与x轴交于B(-3,0)、A(1,0)
设直线AC为y=kx+b,则有0=k+b
6=-2k+b解得 k=-2
b=2
∴直线AC为y=-2x+23分
(2)①设P的横坐标为a(-2≤a≤1),则P(a,-2a+2),M(a,-2a2-4a+6)4分
∴PM=-2a2-4a+6-(-2a+2)=-2a2-2a+4=-2a2+a+14+92
=-2a+122+92
∴当a=-12时,PM的最大值为926分
②M1(0,6)7分
 M2-14,6789分
M2-14,6789分
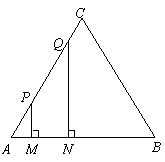
109.(2009年宁夏)26.(10分)
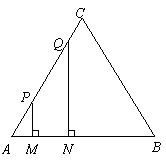
已知:等边三角形 的边长为4厘米,长为1厘米的线段
的边长为4厘米,长为1厘米的线段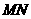 在
在 的边
的边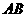 上沿
上沿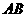 方向以1厘米/秒的速度向
方向以1厘米/秒的速度向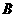 点运动(运动开始时,点
点运动(运动开始时,点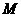 与点
与点 重合,点
重合,点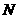 到达点
到达点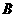 时运动终止),过点
时运动终止),过点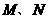 分别作
分别作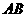 边的垂线,与
边的垂线,与 的其它边交于
的其它边交于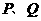 两点,线段
两点,线段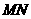 运动的时间为
运动的时间为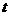 秒.
秒.
(1)线段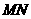 在运动的过程中,
在运动的过程中,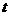 为何值时,四边形
为何值时,四边形 恰为矩形?并求出该矩形的面积;
恰为矩形?并求出该矩形的面积;
 (2)线段
(2)线段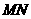 在运动的过程中,四边形
在运动的过程中,四边形 的面积为
的面积为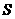 ,运动的时间为
,运动的时间为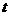 .求四边形
.求四边形 的面积
的面积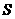 随运动时间
随运动时间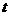 变化的函数关系式,并写出自变量
变化的函数关系式,并写出自变量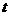 的取值范围.
的取值范围.
(2009年宁夏26题解析)(1)过点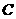 作
作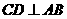 ,垂足为
,垂足为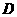 .
.
则 ,
,
 当
当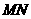 运动到被
运动到被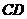 垂直平分时,四边形
垂直平分时,四边形 是矩形,
是矩形,
即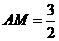 时,四边形
时,四边形 是矩形,
是矩形,
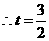 秒时,四边形
秒时,四边形 是矩形.
是矩形.
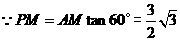 ,
,
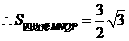 ····································································································· 4分
····································································································· 4分
(2)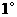 当
当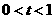 时,
时,

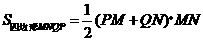

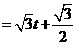 ······························································ 6分
······························································ 6分
 当
当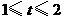 时
时
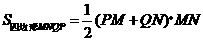

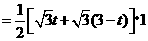
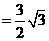 ···································································· 8分
···································································· 8分
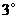 当
当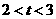 时,
时,
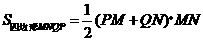
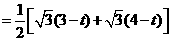
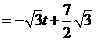 ······················································· 10分
······················································· 10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com