
题目列表(包括答案和解析)
64.(2009年江西)25.如图1,在等腰梯形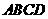 中,
中,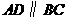 ,
,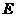 是
是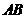 的中点,过点
的中点,过点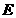 作
作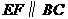 交
交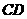 于点
于点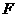 .
.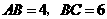 ,
,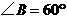 .
.
(1)求点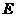 到
到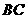 的距离;
的距离;
(2)点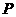 为线段
为线段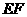 上的一个动点,过
上的一个动点,过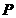 作
作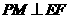 交
交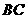 于点
于点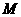 ,过
,过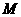 作
作 交折线
交折线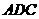 于点
于点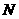 ,连结
,连结 ,设
,设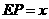 .
.
①当点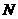 在线段
在线段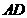 上时(如图2),
上时(如图2),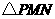 的形状是否发生改变?若不变,求出
的形状是否发生改变?若不变,求出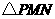 的周长;若改变,请说明理由;
的周长;若改变,请说明理由;
②当点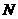 在线段
在线段 上时(如图3),是否存在点
上时(如图3),是否存在点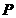 ,使
,使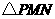 为等腰三角形?若存在,请求出所有满足要求的
为等腰三角形?若存在,请求出所有满足要求的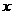 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
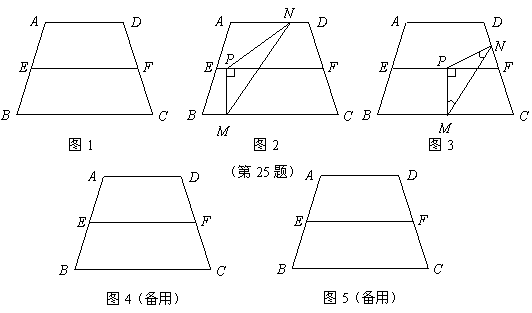
(2009年江西25题解析)(1)如图1,过点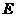 作
作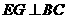 于点
于点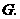 1分
1分
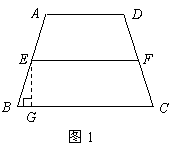 ∵
∵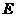 为
为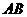 的中点,
的中点,
∴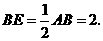
在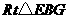 中,
中,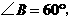 ∴
∴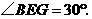 ············· 2分
············· 2分
∴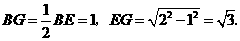
即点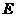 到
到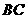 的距离为
的距离为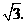 ··········································· 3分
··········································· 3分
(2)①当点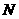 在线段
在线段 上运动时,
上运动时,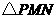 的形状不发生改变.
的形状不发生改变.
∵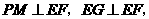 ∴
∴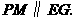
∵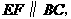 ∴
∴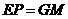 ,
,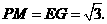
同理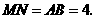 ······························································································· 4分
······························································································· 4分
如图2,过点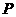 作
作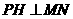 于
于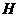 ,∵
,∵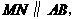
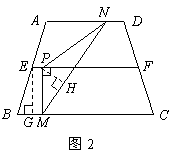 ∴
∴
∴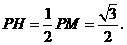
∴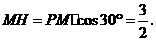
则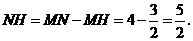
在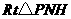 中,
中,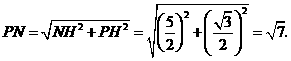
∴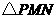 的周长=
的周长=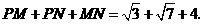 ············································· 6分
············································· 6分
②当点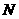 在线段
在线段 上运动时,
上运动时,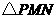 的形状发生改变,但
的形状发生改变,但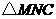 恒为等边三角形.
恒为等边三角形.
当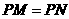 时,如图3,作
时,如图3,作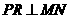 于
于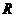 ,则
,则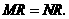
类似①,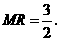
∴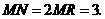 ································································································ 7分
································································································ 7分
∵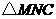 是等边三角形,∴
是等边三角形,∴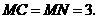
此时,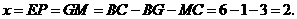 ········································· 8分
········································· 8分
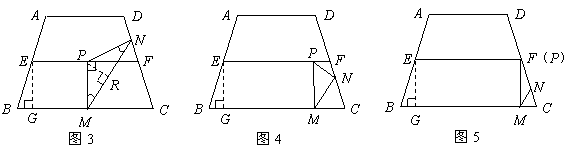
 当
当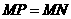 时,如图4,这时
时,如图4,这时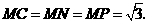
此时,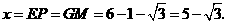
当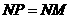 时,如图5,
时,如图5,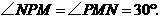
则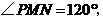 又
又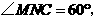
∴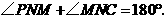
因此点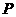 与
与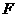 重合,
重合,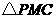 为直角三角形.
为直角三角形.
∴
此时,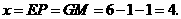
综上所述,当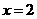 或4或
或4或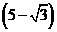 时,
时,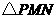 为等腰三角形.························ 10分
为等腰三角形.························ 10分
63.(2009年山东德州)23. (本题满分10分)
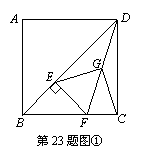
已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)求证:EG=CG;
(2)将图①中△BEF绕B点逆时针旋转45º,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
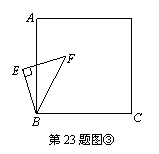
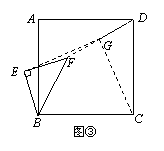
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)
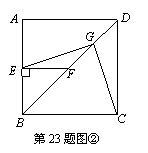
(2009年山东德州23题解析)解:(1)证明:在Rt△FCD中,
∵G为DF的中点,∴
CG=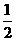 FD.………… 1分
FD.………… 1分
同理,在Rt△DEF中,
EG=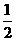 FD. ………………2分
FD. ………………2分
∴ CG=EG.…………………3分
(2)(1)中结论仍然成立,即EG=CG.…………………………4分
证法一:连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点.
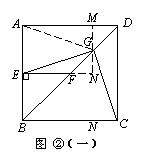 在△DAG与△DCG中,
在△DAG与△DCG中,
∵ AD=CD,∠ADG=∠CDG,DG=DG,
∴ △DAG≌△DCG.
∴ AG=CG.………………………5分
在△DMG与△FNG中,
∵ ∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,
∴ △DMG≌△FNG.
∴ MG=NG
在矩形AENM中,AM=EN. ……………6分
在Rt△AMG 与Rt△ENG中,
∵ AM=EN, MG=NG,
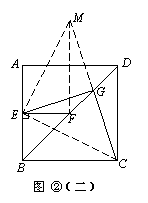 ∴ △AMG≌△ENG.
∴ △AMG≌△ENG.
∴ AG=EG.
∴ EG=CG. ……………………………8分
证法二:延长CG至M,使MG=CG,
连接MF,ME,EC, ……………………4分
在△DCG 与△FMG中,
∵FG=DG,∠MGF=∠CGD,MG=CG,
∴△DCG ≌△FMG.
∴MF=CD,∠FMG=∠DCG.
∴MF∥CD∥AB.………………………5分
∴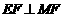 .
.
在Rt△MFE 与Rt△CBE中,
 ∵ MF=CB,EF=BE,
∵ MF=CB,EF=BE,
∴△MFE ≌△CBE.
∴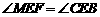 .…………………………………………………6分
.…………………………………………………6分
∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°. …………7分
∴ △MEC为直角三角形.
∵ MG = CG,
∴ EG=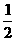 MC.
MC.
∴ 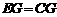 .………………………………8分
.………………………………8分
(3)(1)中的结论仍然成立,
即EG=CG.其他的结论还有:EG⊥CG.……10分
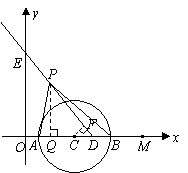
62.(2009年江苏)28.(本题满分12分)如图,已知射线DE与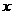 轴和
轴和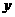 轴分别交于点
轴分别交于点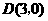 和点
和点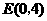 .动点
.动点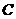 从点
从点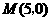 出发,以1个单位长度/秒的速度沿
出发,以1个单位长度/秒的速度沿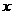 轴向左作匀速运动,与此同时,动点P从点D出发,也以1个单位长度/秒的速度沿射线DE的方向作匀速运动.设运动时间为
轴向左作匀速运动,与此同时,动点P从点D出发,也以1个单位长度/秒的速度沿射线DE的方向作匀速运动.设运动时间为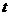 秒.
秒.
(1)请用含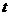 的代数式分别表示出点C与点P的坐标;
的代数式分别表示出点C与点P的坐标;
(2)以点C为圆心、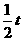 个单位长度为半径的
个单位长度为半径的 与
与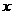 轴交于A、B两点(点A在点B的左侧),连接PA、PB.
轴交于A、B两点(点A在点B的左侧),连接PA、PB.
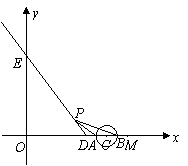 ①当
①当 与射线DE有公共点时,求
与射线DE有公共点时,求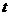 的取值范围;
的取值范围;
②当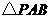 为等腰三角形时,求
为等腰三角形时,求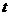 的值.
的值.
(2009年江苏28题解析)解:(1)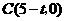 ,
,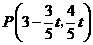 .······················· (2分)
.······················· (2分)
(2)①当 的圆心
的圆心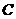 由点
由点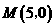 向左运动,使点
向左运动,使点 到点
到点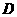 并随
并随 继续向左运动时,
继续向左运动时,
有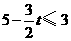 ,即
,即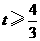 .
.
当点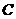 在点
在点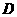 左侧时,过点
左侧时,过点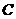 作
作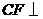 射线
射线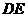 ,垂足为
,垂足为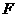 ,则由
,则由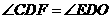 ,
,
得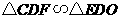 ,则
,则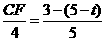 .解得
.解得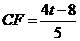 .
.
由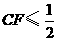
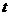 ,即
,即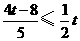 ,解得
,解得 .
.
 当
当 与射线
与射线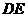 有公共点时,
有公共点时,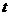 的取值范围为
的取值范围为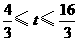 .··························· (5分)
.··························· (5分)
②当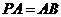 时,过
时,过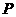 作
作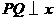 轴,垂足为
轴,垂足为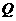 ,有
,有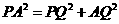
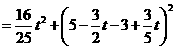 .
.
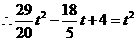 ,即
,即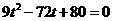 .
.
 解得
解得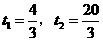 .····································· (7分)
.····································· (7分)
当 时,有
时,有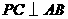 ,
,
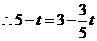 .解得
.解得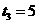 .·························· (9分)
.·························· (9分)
当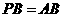 时,有
时,有
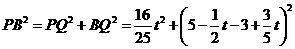 .
.
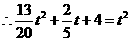 ,即
,即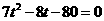 .
.
解得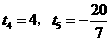 (不合题意,舍去).························································· (11分)
(不合题意,舍去).························································· (11分)
 当
当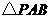 是等腰三角形时,
是等腰三角形时,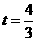 ,或
,或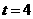 ,或
,或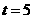 ,或
,或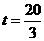 .··············· (12分)
.··············· (12分)
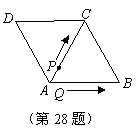
61.(09年吉林)28.如图所示,菱形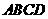 的边长为6厘米,
的边长为6厘米,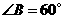 .从初始时刻开始,点
.从初始时刻开始,点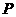 、
、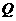 同时从
同时从 点出发,点
点出发,点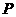 以1厘米/秒的速度沿
以1厘米/秒的速度沿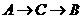 的方向运动,点
的方向运动,点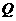 以2厘米/秒的速度沿
以2厘米/秒的速度沿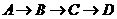 的方向运动,当点
的方向运动,当点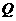 运动到
运动到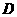 点时,
点时,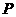 、
、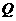 两点同时停止运动,设
两点同时停止运动,设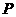 、
、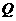 运动的时间为
运动的时间为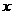 秒时,
秒时,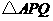 与
与 重叠部分的面积为
重叠部分的面积为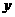 平方厘米(这里规定:点和线段是面积为
平方厘米(这里规定:点和线段是面积为 的三角形),解答下列问题:
的三角形),解答下列问题:
(1)点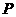 、
、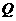 从出发到相遇所用时间是
秒;
从出发到相遇所用时间是
秒;
(2)点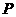 、
、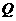 从开始运动到停止的过程中,当
从开始运动到停止的过程中,当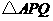 是等边三角形时
是等边三角形时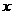 的值是 秒;
的值是 秒;
(3)求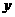 与
与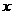 之间的函数关系式.
之间的函数关系式.
(09年吉林28题解析)解:(1)6.···································································· (1分)
(2)8.················································································································ (3分)
(3)①当0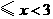 时,
时,
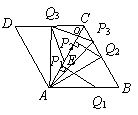
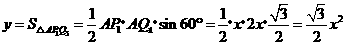 . ··································· (5分)
. ··································· (5分)
②当3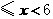 时,
时,
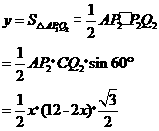
=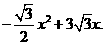 ·································································································· (7分)
·································································································· (7分)
③当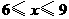 时,设
时,设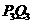 与
与 交于点
交于点 .
.
(解法一)
过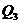 作
作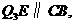 则
则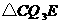 为等边三角形.
为等边三角形.
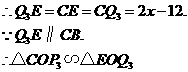
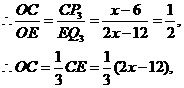
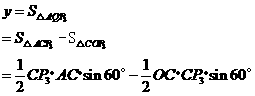
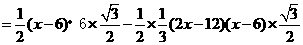 .
.
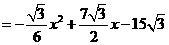 .··············································································· (10分)
.··············································································· (10分)
(解法二)
如右图,过点 作
作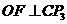 于点
于点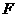 ,
, ,于点
,于点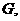
过点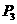 作
作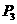
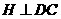 交
交 延长线于点
延长线于点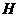 .
.
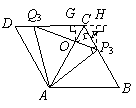
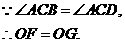
又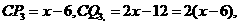
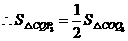
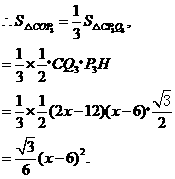
又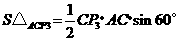
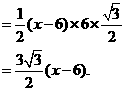
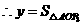
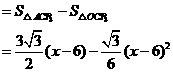
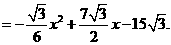 ·················································································· (10分)
·················································································· (10分)
75.(2009年山西太原)29.(本小题满分12分)
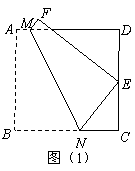 问题解决
问题解决
如图(1),将正方形纸片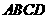 折叠,使点
折叠,使点 落在
落在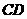 边上一点
边上一点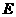 (不与点
(不与点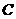 ,
,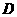 重合),压平后得到折痕
重合),压平后得到折痕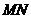 .当
.当 时,求
时,求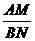 的值.
的值.
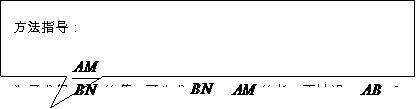
类比归纳
在图(1)中,若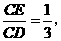 则
则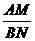 的值等于 ;若
的值等于 ;若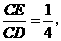 则
则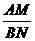 的值等于 ;若
的值等于 ;若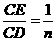 (
(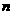 为整数),则
为整数),则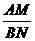 的值等于 .(用含
的值等于 .(用含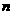 的式子表示)
的式子表示)
联系拓广
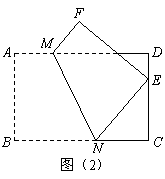 如图(2),将矩形纸片
如图(2),将矩形纸片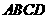 折叠,使点
折叠,使点 落在
落在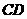 边上一点
边上一点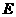 (不与点
(不与点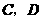 重合),压平后得到折痕
重合),压平后得到折痕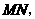 设
设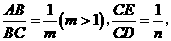 则
则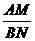 的值等于 .(用含
的值等于 .(用含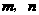 的式子表示)
的式子表示)
(2009年山西太原29题解析)解:方法一:如图(1-1),连接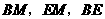 .
.
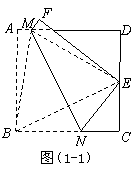
由题设,得四边形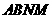 和四边形
和四边形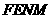 关于直线
关于直线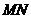 对称.
对称.
∴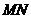 垂直平分
垂直平分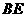 .∴
.∴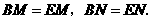 ··········································· 1分
··········································· 1分
∵四边形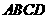 是正方形,∴
是正方形,∴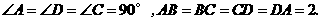
∵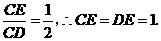 设
设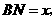 则
则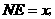
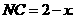
在 中,
中, .
.
∴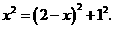 解得
解得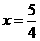 ,即
,即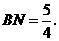 ················································ 3分
················································ 3分
在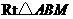 和在
和在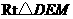 中,
中,
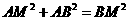 ,
,
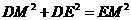 ,
,

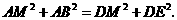 ······································································· 5分
······································································· 5分
设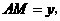 则
则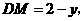 ∴
∴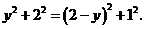
解得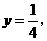 即
即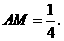 ················································································· 6分
················································································· 6分
∴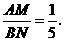 ··································································································· 7分
··································································································· 7分
方法二:同方法一,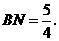 ········································································· 3分
········································································· 3分
如图(1-2),过点 做
做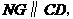 交
交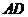 于点
于点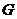 ,连接
,连接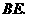

∵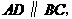 ∴四边形
∴四边形 是平行四边形.
是平行四边形.
∴
同理,四边形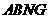 也是平行四边形.∴
也是平行四边形.∴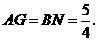
∵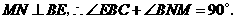
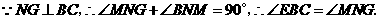
在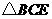 与
与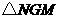 中
中
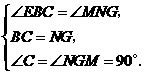 ∴
∴ ····························· 5分
····························· 5分
∵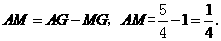 ······························································ 6分
······························································ 6分
∴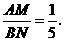 ································································································· 7分
································································································· 7分
类比归纳
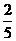 (或
(或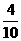 );
); ;
; 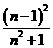 ··········································································· 10分
··········································································· 10分
联系拓广
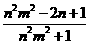 ···································································································· 12分
···································································································· 12分
74.(2009年山东德州)23. (本题满分10分)
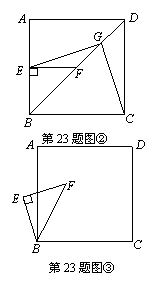
已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)求证:EG=CG;
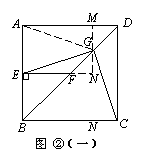
(2)将图①中△BEF绕B点逆时针旋转45º,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
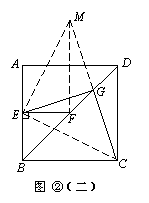
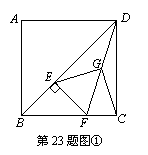 (3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)
(2009年山东德州23题解析)解:(1)证明:在Rt△FCD中,
∵G为DF的中点,∴
CG=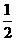 FD.………… 1分
FD.………… 1分
同理,在Rt△DEF中,
EG=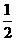 FD. ………………2分
FD. ………………2分
∴ CG=EG.…………………3分
(2)(1)中结论仍然成立,即EG=CG.…………………………4分
证法一:连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点.
 在△DAG与△DCG中,
在△DAG与△DCG中,
∵ AD=CD,∠ADG=∠CDG,DG=DG,
∴ △DAG≌△DCG.
∴ AG=CG.………………………5分
在△DMG与△FNG中,
∵ ∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,
∴ △DMG≌△FNG.
∴ MG=NG
在矩形AENM中,AM=EN. ……………6分
在Rt△AMG 与Rt△ENG中,
∵ AM=EN, MG=NG,
∴ △AMG≌△ENG.
∴ AG=EG.
 ∴ EG=CG. ……………………………8分
∴ EG=CG. ……………………………8分
证法二:延长CG至M,使MG=CG,
连接MF,ME,EC, ……………………4分
在△DCG 与△FMG中,
∵FG=DG,∠MGF=∠CGD,MG=CG,
∴△DCG ≌△FMG.
∴MF=CD,∠FMG=∠DCG.
∴MF∥CD∥AB.………………………5分
∴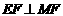 .
.
在Rt△MFE 与Rt△CBE中,
∵ MF=CB,EF=BE,
∴△MFE ≌△CBE.
∴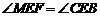 .…………………………………………………6分
.…………………………………………………6分
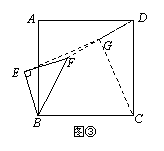 ∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°. …………7分
∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°. …………7分
∴ △MEC为直角三角形.
∵ MG = CG,
∴ EG=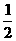 MC.
MC.
∴ 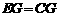 .………………………………8分
.………………………………8分
(3)(1)中的结论仍然成立,
即EG=CG.其他的结论还有:EG⊥CG.……10分
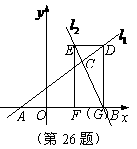
73.(2009年山西)26.(本题14分)如图,已知直线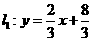 与直线
与直线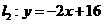 相交于点
相交于点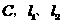 分别交
分别交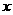 轴于
轴于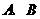 两点.矩形
两点.矩形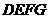 的顶点
的顶点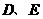 分别在直线
分别在直线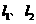 上,顶点
上,顶点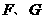 都在
都在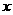 轴上,且点
轴上,且点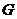 与点
与点 重合.
重合.
(1)求 的面积;
的面积;
(2)求矩形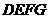 的边
的边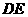 与
与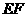 的长;
的长;
 (3)若矩形
(3)若矩形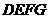 从原点出发,沿
从原点出发,沿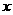 轴的反方向以每秒1个单位长度的速度平移,设移动时间为
轴的反方向以每秒1个单位长度的速度平移,设移动时间为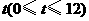 秒,矩形
秒,矩形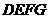 与
与 重叠部分的面积为
重叠部分的面积为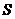 ,求
,求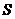 关于
关于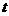 的函数关系式,并写出相应的
的函数关系式,并写出相应的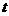 的取值范围.
的取值范围.
(2009年山西26题解析)(1)解:由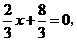 得
得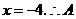 点坐标为
点坐标为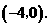
由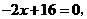 得
得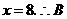 点坐标为
点坐标为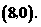
∴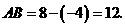 ··················································································· (2分)
··················································································· (2分)
由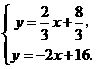 解得
解得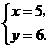 ∴
∴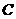 点的坐标为
点的坐标为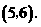 ···································· (3分)
···································· (3分)
∴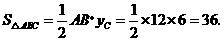 ··························································· (4分)
··························································· (4分)
(2)解:∵点 在
在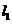 上且
上且
∴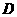 点坐标为
点坐标为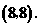 ······················································································ (5分)
······················································································ (5分)
又∵点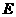 在
在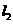 上且
上且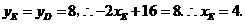
∴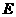 点坐标为
点坐标为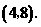 ······················································································ (6分)
······················································································ (6分)
∴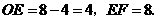 ··········································································· (7分)
··········································································· (7分)
(3)解法一: 当
当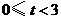 时,如图1,矩形
时,如图1,矩形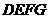 与
与 重叠部分为五边形
重叠部分为五边形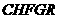 (
(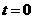 时,为四边形
时,为四边形 ).过
).过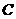 作
作 于
于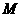 ,则
,则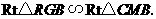

∴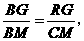 即
即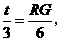 ∴
∴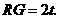
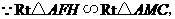
∴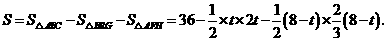
即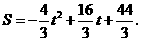 ··································································· (10分)
··································································· (10分)
96.(2009年仙桃市、天门市、潜江市、江汉油田)(本题暂无答案)25.(本题满分12分)如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=3,BC=4,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D 出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交AC于点M,交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.
(1)求NC,MC的长(用t的代数式表示);
(2)当t为何值时,四边形PCDQ构成平行四边形?
(3)是否存在某一时刻,使射线QN恰好将△ABC的面积和周长同时平分?若存在,求出此时t的值;若不存在,请说明理由;
 (4)探究:t为何值时,△PMC为等腰三角形?
(4)探究:t为何值时,△PMC为等腰三角形?
95.(2009年天津)26.(本小题10分)
已知函数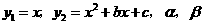 为方程
为方程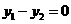 的两个根,点
的两个根,点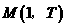 在函数
在函数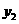 的图象上.
的图象上.
(Ⅰ)若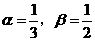 ,求函数
,求函数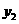 的解析式;
的解析式;
(Ⅱ)在(Ⅰ)的条件下,若函数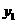 与
与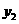 的图象的两个交点为
的图象的两个交点为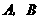 ,当
,当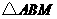 的面积为
的面积为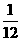 时,求
时,求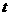 的值;
的值;
(Ⅲ)若 ,当
,当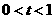 时,试确定
时,试确定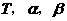 三者之间的大小关系,并说明理由.
三者之间的大小关系,并说明理由.
(2009年天津26题解析)本小题满分10分.
解(Ⅰ)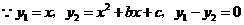 ,
,
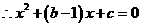 .··························································································· 1分
.··························································································· 1分
将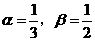 分别代入
分别代入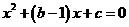 ,得
,得
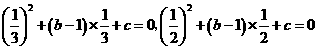 ,
,
解得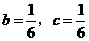 .
.
 函数
函数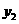 的解析式为
的解析式为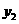
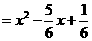 .······························································· 3分
.······························································· 3分
(Ⅱ)由已知,得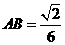 ,设
,设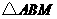 的高为
的高为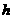 ,
,
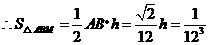 ,即
,即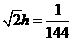 .
.
根据题意,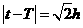 ,
,
由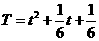 ,得
,得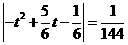 .
.
当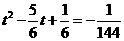 时,解得
时,解得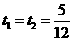 ;
;
当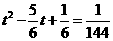 时,解得
时,解得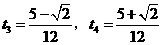 .
.
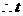 的值为
的值为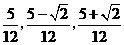 .··············································································· 6分
.··············································································· 6分
(Ⅲ)由已知,得
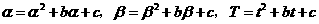 .
.
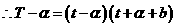 ,
,
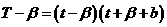 ,
,
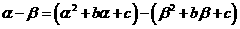 ,化简得
,化简得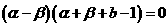 .
.
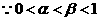 ,得
,得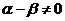 ,
, 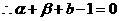 .
.
有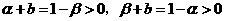 .
.
又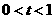 ,
,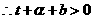 ,
,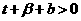 ,
,
 当
当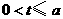 时,
时,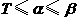 ;
;
当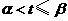 时,
时,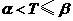 ;
;
当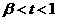 时,
时,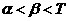 .························································································· 10分
.························································································· 10分
94.(2009年新疆维吾尔自治区)24.(12分)某公交公司的公共汽车和出租车每天从乌鲁木齐市出发往返于乌鲁木齐市和石河子市两地,出租车比公共汽车多往返一趟,如图表示出租车距乌鲁木齐市的路程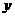 (单位:千米)与所用时间
(单位:千米)与所用时间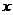 (单位:小时)的函数图象.已知公共汽车比出租车晚1小时出发,到达石河子市后休息2小时,然后按原路原速返回,结果比出租车最后一次返回乌鲁木齐早1小时.
(单位:小时)的函数图象.已知公共汽车比出租车晚1小时出发,到达石河子市后休息2小时,然后按原路原速返回,结果比出租车最后一次返回乌鲁木齐早1小时.
(1)请在图中画出公共汽车距乌鲁木齐市的路程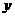 (千米)与所用时间
(千米)与所用时间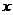 (小时)的函数图象.
(小时)的函数图象.
(2)求两车在途中相遇的次数(直接写出答案)
(3)求两车最后一次相遇时,距乌鲁木齐市的路程.
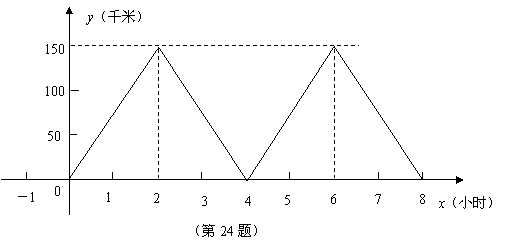
(2009年新疆维吾尔自治区24题解析)24.(12分)解:(1)如图···················· (3分)
(2)2次··············································································································· (5分)
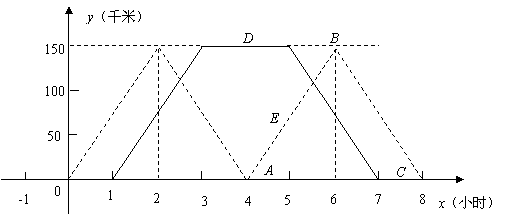
(3)如图,设直线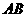 的解析式为
的解析式为 ,
,
 图象过
图象过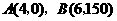 ,
,
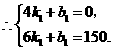
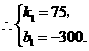
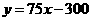 .①································································································ (7分)
.①································································································ (7分)
设直线 的解析式为
的解析式为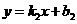 ,
,
 图象过
图象过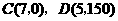 ,
,
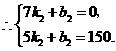
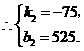

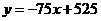 .②·························································································· (7分)
.②·························································································· (7分)
解由①、②组成的方程组得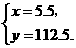
 最后一次相遇时距离乌鲁木齐市的距离为112.5千米.······································ (12分)
最后一次相遇时距离乌鲁木齐市的距离为112.5千米.······································ (12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com