
题目列表(包括答案和解析)
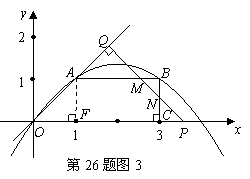
50.(09年湖南长沙)(本题答案暂缺)26.(本题满分10分)
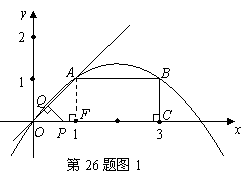
如图,二次函数 (
( )的图象与
)的图象与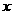 轴交于
轴交于 两点,与
两点,与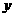 轴相交于点
轴相交于点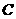 .连结
.连结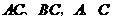 两点的坐标分别为
两点的坐标分别为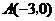 、
、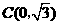 ,且当
,且当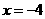 和
和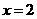 时二次函数的函数值
时二次函数的函数值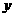 相等.
相等.
(1)求实数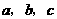 的值;
的值;
(2)若点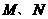 同时从
同时从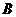 点出发,均以每秒1个单位长度的速度分别沿
点出发,均以每秒1个单位长度的速度分别沿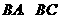 边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为
边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为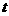 秒时,连结
秒时,连结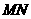 ,将
,将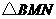 沿
沿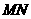 翻折,
翻折,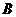 点恰好落在
点恰好落在 边上的
边上的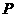 处,求
处,求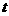 的值及点
的值及点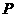 的坐标;
的坐标;
 (3)在(2)的条件下,二次函数图象的对称轴上是否存在点
(3)在(2)的条件下,二次函数图象的对称轴上是否存在点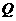 ,使得以
,使得以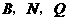 为项点的三角形与
为项点的三角形与 相似?如果存在,请求出点
相似?如果存在,请求出点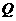 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
49.(09年湖北宜昌)24.已知:直角梯形OABC的四个顶点是O(0,0),A(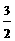 ,1), B(s,t),C(
,1), B(s,t),C(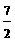 ,0),抛物线y=x2+mx-m的顶点P是直角梯形OABC内部或边上的一个动点,m为常数.
,0),抛物线y=x2+mx-m的顶点P是直角梯形OABC内部或边上的一个动点,m为常数.
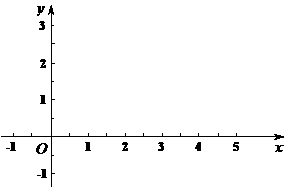
(1)求s与t的值,并在直角坐标系中画出直角梯形OABC;
(2)当抛物线y=x2+mx-m与直角梯形OABC的边AB相交时,求m的取值范围.
 (12分)
(12分)
(09年湖北宜昌24题解析)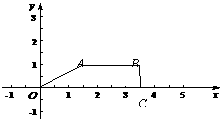 (1)如图,在坐标系中标出O,A,C三点,连接OA,OC.
(1)如图,在坐标系中标出O,A,C三点,连接OA,OC.
∵∠AOC≠90°, ∴∠ABC=90°,
故BC⊥OC, BC⊥AB,∴B(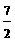 ,1).(1分,)
,1).(1分,)
即s=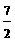 ,t=1.直角梯形如图所画.(2分)
,t=1.直角梯形如图所画.(2分)
(大致说清理由即可)
(2)由题意,y=x2+mx-m与 y=1(线段AB)相交,
得,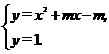 (3分)∴1=x2+mx-m,
(3分)∴1=x2+mx-m,
由 (x-1)(x+1+m)=0,得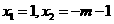 .
.
∵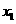 =1<
=1<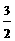 ,不合题意,舍去. (4分)
,不合题意,舍去. (4分)
∴抛物线y=x2+mx-m与AB边只能相交于( ,1),
,1),
∴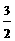 ≤-m-1≤
≤-m-1≤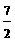 ,∴
,∴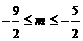 . ①(5分)
. ①(5分)
又∵顶点P(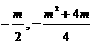 )是直角梯形OABC的内部和其边上的一个动点,
)是直角梯形OABC的内部和其边上的一个动点,
∴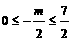 ,即
,即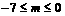 . ② (6分)
. ② (6分)
∵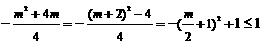 ,
,
(或者抛物线y=x2+mx-m顶点的纵坐标最大值是1)
∴点P一定在线段AB的下方. (7分)
又∵点P在x轴的上方,
∴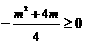 ,
,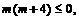
∴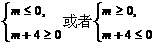 . (*8分)
. (*8分)
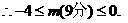 ③(9分)
③(9分)
又∵点P在直线y=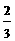 x的下方,∴
x的下方,∴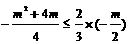 ,(10分)即
,(10分)即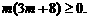
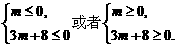 (*8分处评分后,此处不重复评分)
(*8分处评分后,此处不重复评分)
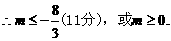 ④
④
由①②③④ ,得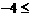
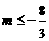 .(12分)
.(12分)
说明:解答过程,全部不等式漏写等号的扣1分,个别漏写的酌情处理.
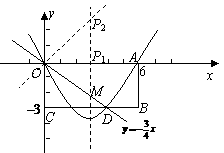
72.(2009年青海)28.矩形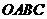 在平面直角坐标系中位置如图13所示,
在平面直角坐标系中位置如图13所示,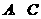 两点的坐标分别为
两点的坐标分别为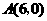 ,
,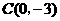 ,直线
,直线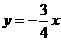 与
与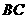 边相交于
边相交于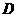 点.
点.
(1)求点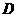 的坐标;
的坐标;
(2)若抛物线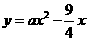 经过点
经过点 ,试确定此抛物线的表达式;
,试确定此抛物线的表达式;
(3)设(2)中的抛物线的对称轴与直线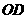 交于点
交于点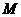 ,点
,点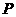 为对称轴上一动点,以
为对称轴上一动点,以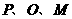 为顶点的三角形与
为顶点的三角形与 相似,求符合条件的点
相似,求符合条件的点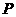 的坐标.
的坐标.
(2009年青海26题解析)解:(1)点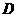 的坐标为
的坐标为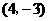 .································ (2分)
.································ (2分)
(2)抛物线的表达式为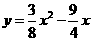 .······························································· (4分)
.······························································· (4分)
 (3)抛物线的对称轴与
(3)抛物线的对称轴与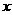 轴的交点
轴的交点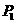 符合条件.
符合条件.
∵ ,
,
∴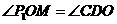 .
.
∵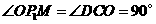 ,
,
∴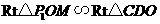 .··························· (6分)
.··························· (6分)
∵抛物线的对称轴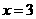 ,
,
∴点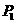 的坐标为
的坐标为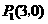 .····················································································· (7分)
.····················································································· (7分)
过点 作
作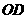 的垂线交抛物线的对称轴于点
的垂线交抛物线的对称轴于点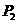 .
.
∵对称轴平行于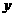 轴,
轴,
∴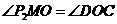 .
.
∵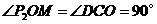 ,
,
∴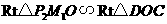 .············································································· (8分)
.············································································· (8分)
∴点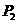 也符合条件,
也符合条件,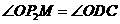 .
.
∴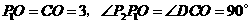 ,
,
∴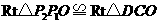 .··············································································· (9分)
.··············································································· (9分)
∴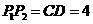 .
.
∵点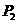 在第一象限,
在第一象限,
∴点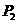 的坐标为
的坐标为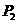
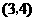 ,
,
∴符合条件的点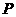 有两个,分别是
有两个,分别是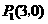 ,
,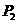
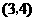 .········································ (11分)
.········································ (11分)
71.(2009年内蒙古呼和浩特)25.(10分)某超市经销一种销售成本为每件40元的商品.据市场调查分析,如果按每件50元销售,一周能售出500件;若销售单价每涨1元,每周销量就减少10件.设销售单价为x元(x≥50),一周的销售量为y件.
(1)写出y与x的函数关系式(标明x的取值范围);
(2)设一周的销售利润为S,写出S与x的函数关系式,并确定当单价在什么范围内变化时,利润随着单价的增大而增大?
(3)在超市对该种商品投入不超过10000元的情况下,使得一周销售例如达到8000元,销售单价应定为多少?
(2009年内蒙古呼和浩特25题解析)解:(1)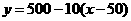
=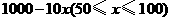 ································································ 3分
································································ 3分
(2)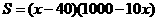
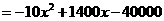
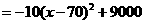
当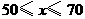 时,利润随着单价的增大而增大.······························································ 6分
时,利润随着单价的增大而增大.······························································ 6分
(3)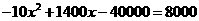
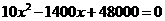
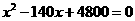
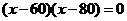
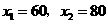 ················································································································ 8分
················································································································ 8分
当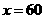 时,成本=
时,成本=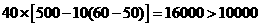 不符合要求,舍去.
不符合要求,舍去.
当 时,成本=
时,成本=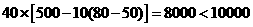 符合要求.
符合要求.
 销售单价应定为80元,才能使得一周销售利润达到8000元的同时,投入不超过10000元. 10分
销售单价应定为80元,才能使得一周销售利润达到8000元的同时,投入不超过10000元. 10分
70.(2009年内蒙古包头)26.(本小题满分12分)
已知二次函数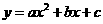 (
(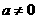 )的图象经过点
)的图象经过点 ,
,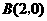 ,
,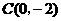 ,直线
,直线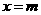 (
(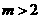 )与
)与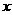 轴交于点
轴交于点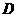 .
.
(1)求二次函数的解析式;
(2)在直线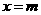 (
(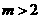 )上有一点
)上有一点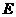 (点
(点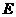 在第四象限),使得
在第四象限),使得 为顶点的三角形与以
为顶点的三角形与以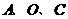 为顶点的三角形相似,求
为顶点的三角形相似,求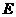 点坐标(用含
点坐标(用含 的代数式表示);
的代数式表示);
(3)在(2)成立的条件下,抛物线上是否存在一点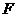 ,使得四边形
,使得四边形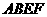 为平行四边形?若存在,请求出
为平行四边形?若存在,请求出 的值及四边形
的值及四边形 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
(2009年内蒙古包头26题解析)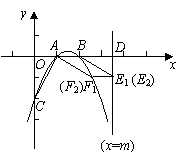 解:(1)根据题意,得
解:(1)根据题意,得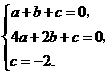
解得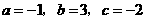 .
.
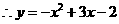 .······························· (2分)
.······························· (2分)
(2)当 时,
时,
得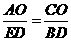 或
或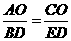 ,
,
∵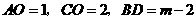 ,
,
当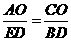 时,得
时,得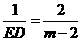 ,
,
∴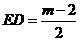 ,
,
∵点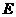 在第四象限,∴
在第四象限,∴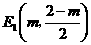 .································································ (4分)
.································································ (4分)
当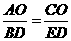 时,得
时,得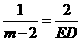 ,∴
,∴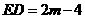 ,
,
∵点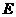 在第四象限,∴
在第四象限,∴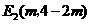 .································································ (6分)
.································································ (6分)
(3)假设抛物线上存在一点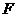 ,使得四边形
,使得四边形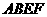 为平行四边形,则
为平行四边形,则
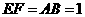 ,点
,点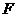 的横坐标为
的横坐标为 ,
,
当点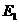 的坐标为
的坐标为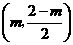 时,点
时,点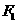 的坐标为
的坐标为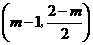 ,
,
∵点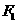 在抛物线的图象上,
在抛物线的图象上,
∴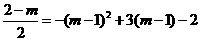 ,
,
∴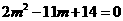 ,
,
∴ ,
,
∴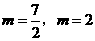 (舍去),
(舍去),
∴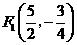 ,
,
∴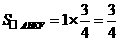 .························································································· (9分)
.························································································· (9分)
当点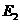 的坐标为
的坐标为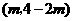 时,点
时,点 的坐标为
的坐标为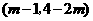 ,
,
∵点 在抛物线的图象上,
在抛物线的图象上,
∴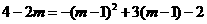 ,
,
∴ ,
,
∴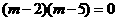 ,∴
,∴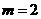 (舍去),
(舍去),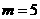 ,
,
∴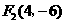 ,
,
∴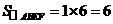 .························································································· (12分)
.························································································· (12分)
注:各题的其它解法或证法可参照该评分标准给分.
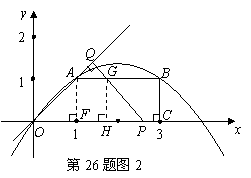
69.(2009年辽宁铁岭)26.如图所示,已知在直角梯形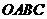 中,
中,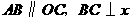 轴于点
轴于点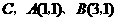 .动点
.动点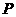 从
从 点出发,沿
点出发,沿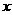 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过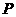 点作
点作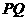 垂直于直线
垂直于直线 ,垂足为
,垂足为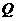 .设
.设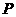 点移动的时间为
点移动的时间为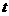 秒(
秒(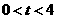 ),
), 与直角梯形
与直角梯形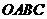 重叠部分的面积为
重叠部分的面积为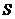 .
.
(1)求经过 三点的抛物线解析式;
三点的抛物线解析式;
(2)求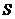 与
与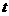 的函数关系式;
的函数关系式;
(3)将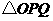 绕着点
绕着点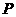 顺时针旋转
顺时针旋转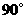 ,是否存在
,是否存在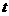 ,使得
,使得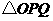 的顶点
的顶点 或
或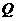 在抛物线上?若存在,直接写出
在抛物线上?若存在,直接写出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(2009年辽宁铁岭26题解析)26.解:(1)法一:由图象可知:抛物线经过原点,
设抛物线解析式为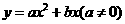 .
.
把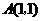 ,
,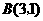 代入上式得:···················································································· 1分
代入上式得:···················································································· 1分
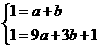 解得
解得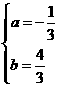 ······················································································· 3分
······················································································· 3分
∴所求抛物线解析式为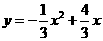 ········································································ 4分
········································································ 4分
法二:∵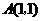 ,
,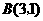 ,
,
∴抛物线的对称轴是直线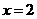 .
.
设抛物线解析式为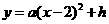 (
(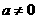 )······························································ 1分
)······························································ 1分
把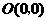 ,
,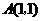 代入得
代入得
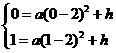 解得
解得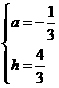 ··········································································· 3分
··········································································· 3分
∴所求抛物线解析式为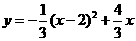 .····························································· 4分
.····························································· 4分
(2)分三种情况:
①当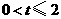 ,重叠部分的面积是
,重叠部分的面积是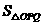 ,过点
,过点 作
作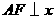 轴于点
轴于点 ,
,
 ∵
∵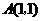 ,在
,在 中,
中,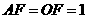 ,
,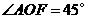 ,
,
在 中,
中,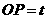 ,
,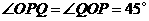 ,
,
∴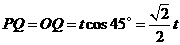 ,
,
 ∴
∴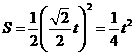 .··············································· 6分
.··············································· 6分
②当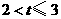 ,设
,设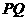 交
交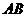 于点
于点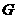 ,作
,作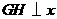 轴于点
轴于点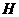 ,
,
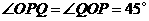 ,则四边形
,则四边形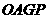 是等腰梯形,
是等腰梯形,
重叠部分的面积是 .
.
∴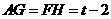 ,
,
∴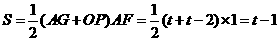 .··········· 8分
.··········· 8分
③当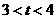 ,设
,设 与
与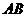 交于点
交于点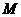 ,交
,交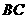 于点
于点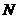 ,重叠部分的面积是
,重叠部分的面积是 .
.
 因为
因为 和
和 都是等腰直角三角形,所以重叠部分的面积是
都是等腰直角三角形,所以重叠部分的面积是
 .
.
∵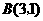 ,
,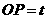 ,
,
∴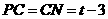 ,
,
∴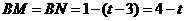 ,
,
∴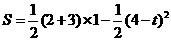
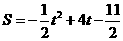 .················································ 10分
.················································ 10分
(3)存在 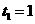 ···································································································· 12分
···································································································· 12分
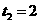 ··································································································· 14分
··································································································· 14分
68.(2009年辽宁锦州)26.如图14,抛物线与x轴交于A(x1,0),B(x2,0)两点,且x1>x2,与y轴交于点C(0,4),其中x1,x2是方程x2-2x-8=0的两个根.
(1)求这条抛物线的解析式;
(2)点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,当△CPE的面积最大时,求点P的坐标;
(3)探究:若点Q是抛物线对称轴上的点,是否存在这样的点Q,使△QBC成为等腰三角形,若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.
(2009年辽宁锦州26题解析)26.解:(1) ∵x2-2x-8=0 ,∴(x-4)(x+2)=0 .∴x1=4,x2=-2.
∴A(4,0) ,B(-2,0). ……1分
又∵抛物线经过点A、B、C,设抛物线解析式为y=ax2+bx+c (a≠0),
∴ ∴
∴ ……3分
……3分
∴所求抛物线的解析式为 . ……4分
. ……4分
(2)设P点坐标为(m,0),过点E作EG⊥x轴于点G.
∵点B坐标为(-2,0),点A坐标(4,0),
∴AB=6, BP=m+2.
∵PE∥AC,
∴△BPE∽△BAC.
∴ .
.
∴ .
.
∴S△CPE= S△CBP- S△EBP
= .
.
∴
 .
.
∴ . ……7分
. ……7分
又∵-2≤m≤4,
∴当m=1时,S△CPE有最大值3.
此时P点的坐标为(1,0). ……9分
(3)存在Q点,其坐标为Q1(1,1),
 ,
,
 ,
,
 ,
,
 .……14分
.……14分
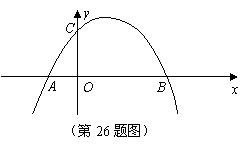
67.(2009年辽宁抚顺)26.已知:如图所示,关于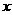 的抛物线
的抛物线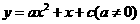 与
与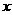 轴交于点
轴交于点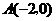 、点
、点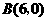 ,与
,与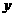 轴交于点
轴交于点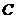 .
.
(1)求出此抛物线的解析式,并写出顶点坐标;
(2)在抛物线上有一点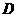 ,使四边形
,使四边形 为等腰梯形,写出点
为等腰梯形,写出点 的坐标,并求出直线
的坐标,并求出直线 的解析式;
的解析式;
 (3)在(2)中的直线
(3)在(2)中的直线 交抛物线的对称轴于点
交抛物线的对称轴于点 ,抛物线上有一动点
,抛物线上有一动点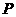 ,
,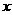 轴上有一动点
轴上有一动点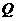 .是否存在以
.是否存在以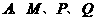 为顶点的平行四边形?如果存在,请直接写出点
为顶点的平行四边形?如果存在,请直接写出点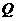 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
(2009年辽宁抚顺26题解析)26.解:(1)根据题意,得
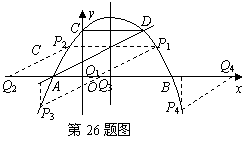
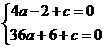 ·········································· 1分
·········································· 1分
解得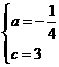 ··············································· 3分
··············································· 3分
 抛物线的解析式为
抛物线的解析式为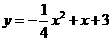 ········· 4分
········· 4分
顶点坐标是(2,4)······································································································ 5分
(2)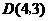 ················································································································ 6分
················································································································ 6分
设直线 的解析式为
的解析式为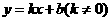
 直线经过点
直线经过点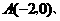 点
点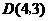
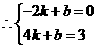 ············································································································· 7分
············································································································· 7分
 ······················································································································ 8分
······················································································································ 8分
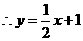 ················································································································ 9分
················································································································ 9分
(3)存在.················································································································ 10分
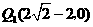 ············································································································ 11分
············································································································ 11分
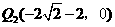 ······································································································· 12分
······································································································· 12分
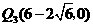 ············································································································ 13分
············································································································ 13分
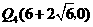 ············································································································ 14分
············································································································ 14分
66.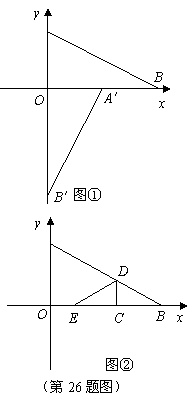 (2009年辽宁朝阳)26.如图
(2009年辽宁朝阳)26.如图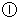 ,点
,点 ,
,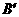 的坐标分别为(2,0)和(0,
的坐标分别为(2,0)和(0,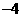 ),将
),将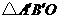 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转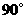 后得
后得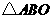 ,点
,点 的对应点是点
的对应点是点 ,点
,点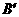 的对应点是点
的对应点是点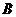 .
.
(1)写出 ,
,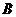 两点的坐标,并求出直线
两点的坐标,并求出直线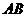 的解析式;
的解析式;
(2)将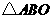 沿着垂直于
沿着垂直于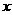 轴的线段
轴的线段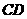 折叠,(点
折叠,(点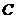 在
在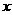 轴上,点
轴上,点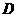 在
在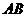 上,点
上,点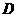 不与
不与 ,
,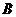 重合)如图
重合)如图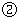 ,使点
,使点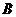 落在
落在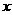 轴上,点
轴上,点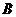 的对应点为点
的对应点为点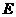 .设点
.设点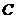 的坐标为(
的坐标为(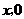 ),
), 与
与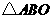 重叠部分的面积为
重叠部分的面积为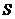 .
.
i)试求出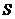 与
与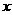 之间的函数关系式(包括自变量
之间的函数关系式(包括自变量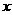 的取值范围);
的取值范围);
ii)当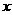 为何值时,
为何值时,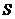 的面积最大?最大值是多少?
的面积最大?最大值是多少?
iii)是否存在这样的点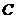 ,使得
,使得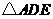 为直角三角形?若存在,直接写出点
为直角三角形?若存在,直接写出点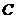 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(2009年辽宁朝阳26题解析)解:(1)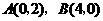 ···································· (2分)
···································· (2分)
设直线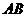 的解析式
的解析式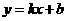 ,则有
,则有
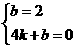 解得
解得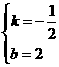
 直线
直线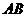 的解析式为
的解析式为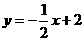 ······································································ (3分)
······································································ (3分)
(2)i)①点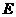 在原点和
在原点和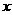 轴正半轴上时,重叠部分是
轴正半轴上时,重叠部分是 .
.
则
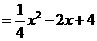
当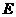 与
与 重合时,
重合时,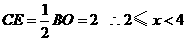 ·················································· (4分)
·················································· (4分)
②当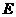 在
在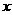 轴的负半轴上时,设
轴的负半轴上时,设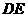 与
与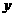 轴交于点
轴交于点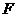 ,则重叠部分为梯形
,则重叠部分为梯形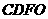 .
.
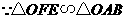
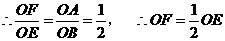
又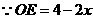
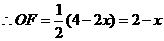
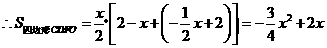 ············································ (5分)
············································ (5分)
当点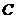 与点
与点 重合时,点
重合时,点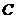 的坐标为
的坐标为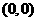
 ············································································································ (6分)
············································································································ (6分)
综合 得
得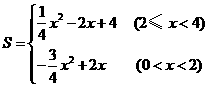 ······················································ (7分)
······················································ (7分)
ii) 当
当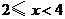 时,
时,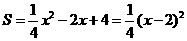
 对称轴是
对称轴是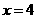
 抛物线开口向上,
抛物线开口向上, 在
在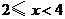 中,
中,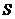 随
随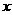 的增大而减小
的增大而减小
 当
当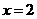 时,
时,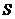 的最大值=
的最大值=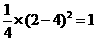 ························································· (8分)
························································· (8分)
 当
当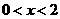 时,
时,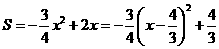
 对称轴是
对称轴是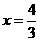
 抛物线开口向下
抛物线开口向下
 当
当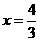 时,
时,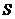 有最大值为
有最大值为 ············································································· (9分)
············································································· (9分)
综合 当
当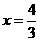 时,
时,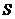 有最大值为
有最大值为 ······························································ (10分)
······························································ (10分)
iii)存在,点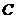 的坐标为
的坐标为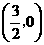 和
和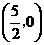 ···························································· (14分)
···························································· (14分)
附:详解: 当
当 以点
以点 为直角顶点时,作
为直角顶点时,作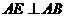 交
交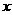 轴负半轴于点
轴负半轴于点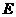 ,
,
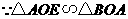
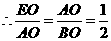
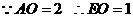
 点
点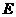 坐标为(
坐标为(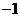 ,0)
,0)
 点
点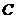 的坐标为
的坐标为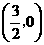
 当
当 以点
以点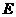 为直角顶点时
为直角顶点时
同样有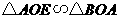
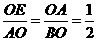
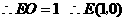
 点
点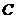 的坐标
的坐标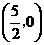
综合①②知满足条件的坐标有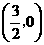 和
和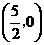 .
.
以上仅提供本试题的一种解法或解题思路,若有不同解法请参照评分标准予以评分.
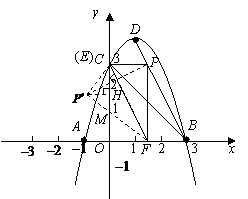
65.(2009年辽宁本溪)26.如图所示,在平面直角坐标系中,抛物线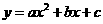 (
(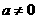 )经过
)经过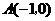 ,
,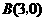 ,
, 三点,其顶点为
三点,其顶点为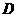 ,连接
,连接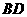 ,点
,点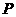 是线段
是线段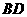 上一个动点(不与
上一个动点(不与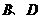 重合),过点
重合),过点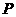 作
作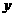 轴的垂线,垂足为
轴的垂线,垂足为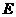 ,连接
,连接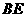 .
.
(1)求抛物线的解析式,并写出顶点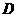 的坐标;
的坐标;
(2)如果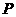 点的坐标为
点的坐标为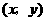 ,
,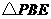 的面积为
的面积为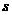 ,求
,求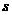 与
与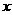 的函数关系式,写出自变量
的函数关系式,写出自变量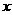 的取值范围,并求出
的取值范围,并求出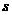 的最大值;
的最大值;
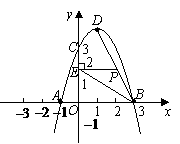 (3)在(2)的条件下,当
(3)在(2)的条件下,当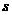 取得最大值时,过点
取得最大值时,过点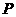 作
作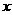 的垂线,垂足为
的垂线,垂足为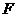 ,连接
,连接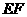 ,把
,把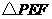 沿直线
沿直线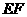 折叠,点
折叠,点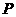 的对应点为
的对应点为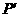 ,请直接写出
,请直接写出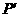 点坐标,并判断点
点坐标,并判断点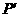 是否在该抛物线上.
是否在该抛物线上.
(2009年辽宁本溪26题解析)26.解:(1)设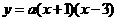 ,·························· 1分
,·························· 1分
把 代入,得
代入,得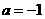 ,························································································· 2分
,························································································· 2分
∴抛物线的解析式为: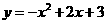 .···································································· 4分
.···································································· 4分
顶点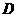 的坐标为
的坐标为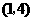 .································································································ 5分
.································································································ 5分
(2)设直线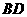 解析式为:
解析式为: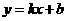 (
(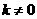 ),把
),把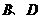 两点坐标代入,
两点坐标代入,
得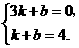 ·············································································································· 6分
·············································································································· 6分
解得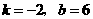 .
.
∴直线 解析式为
解析式为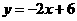 .··············································································· 7分
.··············································································· 7分
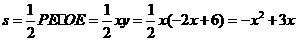 ,······················································· 8分
,······················································· 8分
∴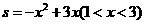 ····························································································· 9分
····························································································· 9分
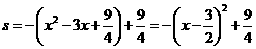 .···························································· 10分
.···························································· 10分
∴当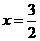 时,
时,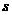 取得最大值,最大值为
取得最大值,最大值为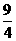 .······························································ 11分
.······························································ 11分
(3)当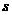 取得最大值,
取得最大值,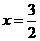 ,
,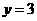 ,∴
,∴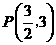 .·················································· 5分
.·················································· 5分
∴四边形 是矩形.
是矩形.
作点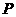 关于直线
关于直线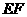 的对称点
的对称点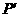 ,连接
,连接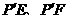 .
.
法一:过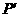 作
作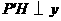 轴于
轴于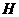 ,
,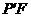 交
交 轴于点
轴于点 .
.
 设
设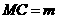 ,则
,则 .
.
在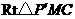 中,由勾股定理,
中,由勾股定理,
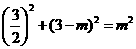 .
.
解得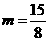 .
.
∵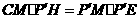 ,
,
∴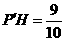 .
.
由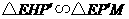 ,可得
,可得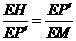 ,
,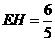 .
.
∴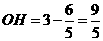 .
.
∴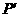 坐标
坐标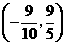 .································································································ 13分
.································································································ 13分
法二:连接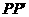 ,交
,交 于点
于点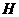 ,分别过点
,分别过点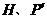 作
作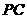 的垂线,垂足为
的垂线,垂足为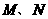 .
.
易证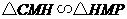 .
.
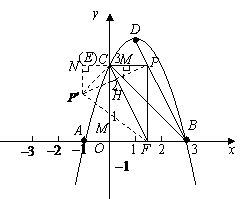 ∴
∴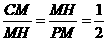 .
.
设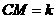 ,则
,则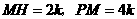 .
.
∴ ,
,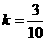 .
.
由三角形中位线定理,
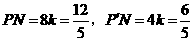 .
.
∴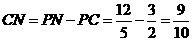 ,即
,即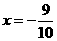 .
.
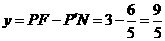
∴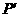 坐标
坐标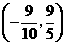 .································································································ 13分
.································································································ 13分
把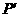 坐标
坐标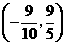 代入抛物线解析式,不成立,所以
代入抛物线解析式,不成立,所以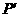 不在抛物线上.·················· 14分
不在抛物线上.·················· 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com